基于ANFIS和减法聚类的动力电池放电峰值功率预测

孙丙香 高 科 姜久春 罗 敏 何婷婷 郑方丹 郭宏榆

（1. 北京交通大学国家能源主动配电网技术研发中心 北京 100044 2. 广东电网公司电力科学研究院 广州 510080 3. 惠州市亿能电子有限公司 惠州 516006）

1 引言

能源危机和环境保护的双重压力，助推了电动汽车和电力储能的大力发展。动力电池作为主要能量源，其短时峰值功率预测的准确性直接关系到使用中的控制策略和可靠性。由于在恒功率充、放电过程中，电池的端电压一直处于变化状态，电流跟随着电压向相反的方向变化；而且电池电压有上、下限限制，在不同的温度和不同的SOC点，电压和电流的变化速率不同。因此，电池短时峰值功率的预测变得复杂。

目前，短时峰值功率预测主要是通过离线数据测试得到数据表，然后通过查表数据插值的办法来进行在线预测。为离线测试电池的峰值功率，业界提出了多种近似的计算方法，并用于评价电池的功率特性。美国FreedomCAR项目提出了电池混合脉冲功率特性（Hybrid Pulse Power Characteristic,HPPC）测试方法[1,2]；日本电动汽车协会标准（Japan Electric Vehicle Association Standards，JEVS）D713—2003《混合动力电动汽车用密闭型镍氢电池的输出密度及输入密度试验方法》中提出了镍氢电池功率的测试方法[3]。两种方法都是采用恒电流脉冲测试，与恒功率测试依然存在差异，测试的结果只适合于评价电池的功率密度，不适用于电池实时功率能力的测试。考虑到实际应用中放电峰值功率的预测对于实际应用意义更大，在综合HPPC和JEVS两种功率测试方法的基础上，本文采用恒功率方法测试电池的脉冲放电功率能力，并通过曲线拟合的方式得到不同条件下的放电峰值功率值。考虑到影响功率能力的因素较多，选取温度、SOC和欧姆内阻为输入量；考虑到模型输入变量和输出变量的非线性耦合关系，采用自适应神经模糊推理系统模型来改进线性插值的预测准确度[4]。全文预测放电峰值功率的总体结构如图1所示。

根据电池电压的使用限制条件，当电池在恒定功率下持续放电t（秒）后端电压正好下降到电池允许的最低工作电压Umin，那么该恒定的功率值即为电池t（秒）的放电峰值功率。因为电池行业一般取10s的功率作为衡量其峰值功率的标准，因此，本文选取t=10s。

2 基本原理

2.1 ANFIS的原理和结构

自适应神经模糊推理系统（Adaptive Neuro-Fuzzy Inference System, ANFIS）直接利用神经网络的优化计算功能，优化模糊控制器的控制参数，改善模糊控制系统的功能。它把神经网络的学习机制引入模糊系统，构成一个带有人类感觉和认知成分的自适应系统。能对训练数据学习，自动产生并修正输入与输出变量的隶属函数，还能够概括最优的模糊规则，同时又能明确理解各层结构与参数的物理意义。

图1 功率预测流程图Fig.1 Flow chart of power prediction

模糊控制系统由模糊控制器和控制对象组成，如图2所示。模糊控制器的基本结构是图2中框中的部分，主要包括四个部分。

ANFIS的典型结构如图3所示[5]。

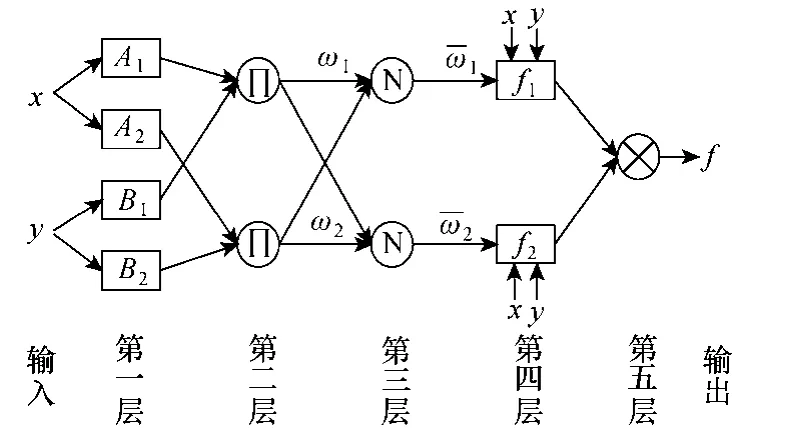
图3 典型ANFIS系统结构Fig.3 Typical ANFIS system structure

图3中，x,y是系统的两个输入，f为推理系统的输出，均为可提供的数据组。其典型模糊推理规则为：

规则R1：IfxisA1andyisB1，Thenf1=p1x+q1y+r1。

规则R2：IfxisA2andyisB2，Thenf2=p2x+q2y+r2。

从图1可以看出，ANFIS网络结构分为五层，网络同一层的每个节点具有相似的功能，用O1,i表示第一层第i个节点的输出，依此类推。

第一层：这一层的节点是自适应节点，以节点函数表示，作用是将输入信号模糊化，确定给定输入满足相应模糊集的程度。节点i具有输出函数[6]

式中，x、y是节点i的输入；Ai、Bi是模糊集，表示“冷”和“热”等模糊意义；μAi(x)和μB(i-2)(y)是模糊集的隶属度函数，表示x，y属于模糊集Ai，Bi（i=1,2）的程度。隶属度函数可以根据需要选取不同的函数，有钟形函数、三角形函数、梯形函数和高斯型函数等。通常选取高斯型函数

式中，{c,σ }是提前参数，需要预先确定，随着前提参数的改变，函数的形状会发生改变，因此要根据不同的映射需要来设置提前参数。

第二层：这一层的节点是固定节点，每个节点用∏表示。其输出是所有输入信号的乘积，表示一条规则的激励强度，即所给的“事实”与该条规则的相符程度。

第三层：这一层的节点是固定节点，每个节点用符号N表示。第i个节点计算第i条规则的激励强度ωi与全部规则值激励强度之和ω的比值，即这一层的输出是对各个规则适用度的归一化。

第四层：这一层的节点是自适应节点，每个节点对应于一条模糊规则，其输出表示在给定激励强度下规则的后件。各节点也拥有节点函数，本层的参数pi、qi和ri称为结论参数。

第五层：该层节点是单节点，是固定节点，标记为∑。它计算所有传来信号之和作为总的最终输出

2.2 减法聚类法

减法聚类（Subtractive Clustering, SC）算法[7,8]是一种用来估计一组数据中的聚类个数以及聚类中心位置的快速实用的单次算法。减法聚类方法将每个数据点都作为可能的聚类中心，然后根据各个数据点周围的数据点密度来计算该点作为聚类中心的可能性。被选为聚类中心的数据点周围具有最高的数据点密度，同时该数据点附近的数据点就被排除作为聚类中心的可能性。在选出第一个聚类中心后，从剩余的可能作为聚类中心的数据点中，继续用类似方法选择下一个中心，直至所有剩余数据点作为聚类中心的可能性低于设定的阈值[9,10]。

假设所有数据点位于一个单位超立方体内，即各维的坐标都在0～1之间，通常指定数据向量的每一维坐标上聚类中心的影响范围在 0.2～0.5。定义数据点Xi的密度为

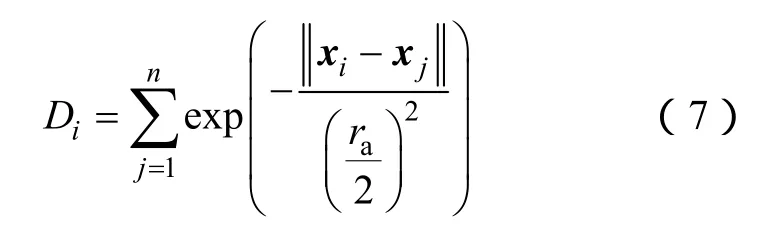
半径ra定义了该点的密度范围，范围外的数据点对密度影响很微小。计算每个数据点密度后，选取密度高的数据点为第一个聚类中心，计此数据点为Xi，DXi为其密度，则其他数据点密度修正为

常数rb定义了一个密度显著减小的范围，通常大于rb。然后重复以上步骤，直至所有剩余的数据点作为聚类中心的可能性低于某一个阈值。当输入变量个数比较多时（≥3），采用减法聚类算法划分输入空间，得到的模糊规则数比采用自适应网格法得到的模糊规则数少得多，输入空间划分更合理、模型简单、训练时间短。并且模糊规则可以一条一条地增加，不易出现过拟合，还能提高模型的泛化能力，提高模型估计准确度。

减法聚类方法根据影响范围等参数进行模糊区间划分，输出层也为一阶线性输出。本文分别采用网格分割法和减法聚类法进行了模型的模糊结构的生成和对比分析。网格分割法选取高斯型隶属函数，模糊区间划分数量为 4、5、5；输出层为一阶线性输出。

3 实验方法

3.1 实验平台及测试对象

搭建的实验平台如图4所示，本平台主要用于电池模块的性能测试和算法验证等，由被测试电池模块，Digatron电池测试系统（主功率模块）、监控PC、高低温箱和数据采集、记录模块组成。测试时，将电池模块放于高低温箱内，调整箱内温度，搁置5h后待电池模块与环境温度一致后启动相应实验；监控 PC通过软件设置来控制主功率模块启动各项测试；数据采集、记录模块记录电压、电流等测试信息。

图4 实验平台Fig.4 Experimental platform

测试对象为12节8Ah锰酸锂单体电池串联的电池模块，数据记录的时间间隔选为50ms。Digatron电池测试系统能够进行恒功率、恒电压以及恒电流等多种工况下的充放电测试，设备的响应时间为50ms。

3.2 峰值功率测试方法

根据电池厂商已经提供的电池电压工作范围，以该充、放电保护电压为依据，控制测试设备以功率P1对电池进行恒功率放电，当电池端电压下降至最低工作电压Umin时停止放电，记录恒功率放电时间t1，如图5所示。调整电池DOD（depth of discharge）至放电前状态，经过充分静置后，将电池的放电功率调整至P2开始恒功率放电至电池允许的最低电压，记录放电时间t2。重复多次循环测试后拟合得到电池在该状态下放电功率P与放电时间t的关系曲线，如图6所示。从拟合曲线中用查询法可得到电池10s峰值放电功率(Pmax,10s)。

图5 恒功率脉冲放电测试曲线Fig.5 Constant power pulse discharge test curve

图6 恒功率脉冲放电测试曲线拟合Fig.6 Curve fitting of discharge test

3.3 欧姆内阻测试方法

电池的内阻是指电池在工作时，电流流过电池内部所受到的阻力。它包括欧姆内阻和极化内阻，其中极化内阻又包括电化学极化内阻和浓差极化内阻。

本文采用了直流充放电内阻测量法[11]对电池进行内阻测试。

图 7描述了电池内阻的测试过程，I0为测试过程中的基准电流，IIR为电流的偏移值，所以脉冲电流大小为I0-IIR和I0+IIR，在脉冲电流的作用下，记下P2和P3时刻电池的端电压，根据电池模型压降和电流的关系得到方程[12]

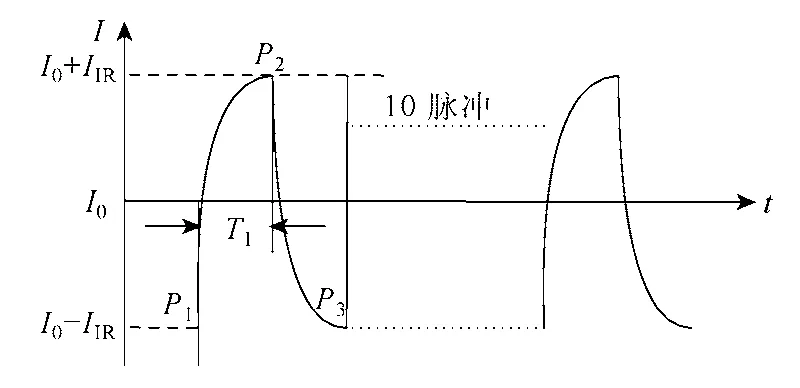
图7 电池内阻测试脉冲电流Fig.7 Pulse current of battery resistance test

由于单次测量可能存在一定的测量误差，文中内阻测量都经过 10次测量剔除坏值后取平均值。其中图中脉冲的宽度T1范围为50μs～80ms之间，本文选取10ms。电流采用正负电流是为了考虑抵消极化效应对测量误差的影响，所以这里测的电池内阻Rin为电池的欧姆内阻。

4 峰值功率预测模型的建立和训练

4.1 输入选取和模型的总体构架

由于电池的峰值功率受多方面的影响，如电池荷电状态SOC、电池温度、电池内阻和充放电脉冲持续时间和充放电状态等，但如果每个量都作为输入量，训练数据会非常庞大，实现起来很困难。

本文中，所选电池用于混合动力轿车，选取电池 SOC、温度和欧姆内阻用来监测电池的峰值功率。因为电池的SOC与开路电压OCV是一一对应的，实际应用中，可以根据SOC-OCV曲线通过OCV的在线监测插值得到电池的SOC。电池内阻特性表现为极化内阻和欧姆内阻两部分，极化内阻复杂多变且不易于在线监测，而欧姆内阻是可以实现在线监测的，温度更是易于测量，故选取欧姆内阻、SOC和温度作为模型的输入。

1978年春，为满足“文化大革命”后高等师范院校教育学教学的需要，五所院校共同编写了一本教育学教材。当时的教材编写主要注重对“文革”时期的教育思想与举措的拨乱反正和向以经济建设为中心转移的新形势需求，很少反思“文革”前的教育理论和实践是否存在问题，更谈不上去研究和提出自己的教育学教材编写的教育观。由于受苏联教育学的影响比较大，出版后受到的批评意见主要表现为“没有跳出凯洛夫《教育学》的框框”。

在确定模型的输入后，以电池的10s放电峰值功率作为输出构造了基于 Sugeno模糊推理的ANFIS模型如图8所示。

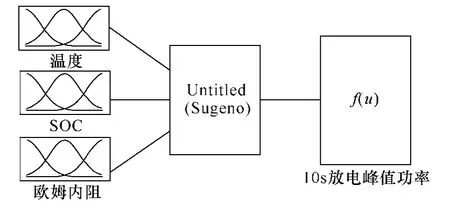
图8 10s放电峰值功率ANFIS模型Fig.8 10 seconds discharge peak power ANFIS model

4.2 采用网格分割法

本文以采用网格分割法[13]的10s放电功率特性模型为例，分别采用单一BP（back propagation）方法和混合训练方法对网络进行训练，对两种训练方法进对比。训练样本如图9所示，温度、SOC和欧姆内阻由主坐标轴（左轴）标注刻度，注意SOC是以 1%为单位，但在训练中将 SOC设为 0.1～0.9，放电峰值功率由副坐标轴（右轴）标注刻度。

图9 训练数据组Fig.9 Training data

训练数据为305对，检验数据也为305对，每组数据包括环境温度、电池SOC、电池欧姆内阻和目标 10s放电峰值功率。将截止误差设置为 5，迭代步数设置为50；三个输入变量的模糊区间划分基于网格生成方式，划分数目为 4、5、5；隶属函数设置为高斯型；输出变量设置为 linear.所得 ANFIS模型结构如图10所示。

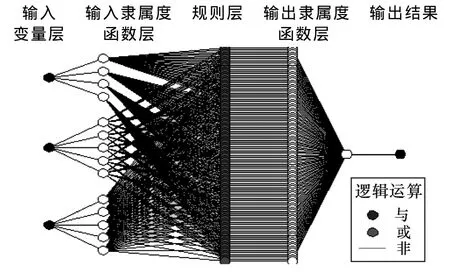
图10 网格法生成的ANFIS模型结构Fig.10 ANFIS model generated by grid method

（1）采用单一 BP训练方法训练网络。采用单一BP方法进行同样设置，训练网络的误差如图11所示。10s放电峰值功率的估计验证如图12所示，其中“*”为模型对训练数据的估计结果，“o”为训练数据实际值。采用单一 BP算法训练网络时，收敛慢且误差大[14]，若想达到 10W 以内的误差，需要几万步甚至更多。

图11 单一BP训练方法误差Fig.11 Error of BP training method

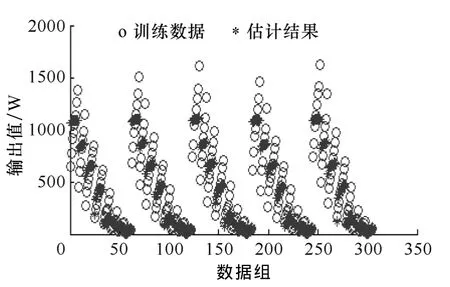
图12 模型输出与真实值对比Fig.12 Comparison of model outputs and true values

（2）采用混合训练方法训练网络。采用混合训练方法训练网络的误差如图13所示，10s放电峰值功率的估计验证如图14所示，其中“*”为模型对训练数据的估计结果，“o”为训练数据实际值。从图13中可以看出，系统误差在10步以内便收敛到8.26W，由于10s峰值功率大部分分布在300W以上，甚至为1 600W以上，因此相对误差很小，从图14也可以看出，ANFIS输出值与实际值相比误差极小。

图13 系统训练后误差曲线Fig.13 Error curve after systematic training

图14 模型输出与真实值对比Fig.14 Comparison of model outputs and true values

为达到最小误差，需要不断调整各输入隶属度函数，在该误差情况下，各输入隶属度函数变化如图 15所示。SOC的隶属度函数在训练后变得比较紧凑，这样会使模糊空间划分更为精确。欧姆内阻的隶属度函数由于疏密程度不同在训练前后发生了明显变化，欧姆内阻大部分集中在10mΩ以内，因此，在10mΩ以内设置紧密的隶属度函数，在10mΩ以上设置稀疏的隶属度函数，这样可以充分减小训练误差。

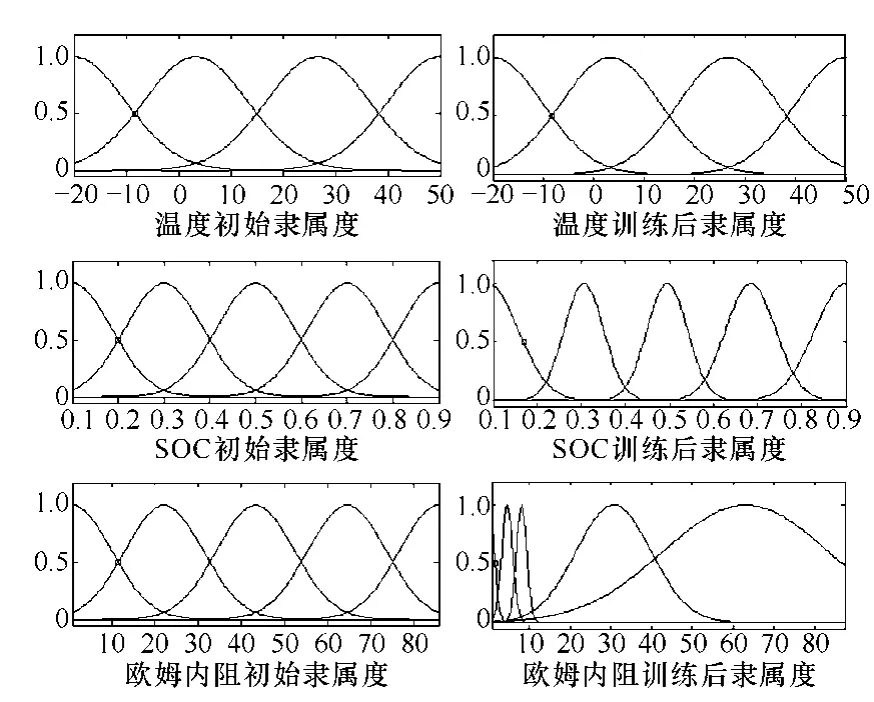
图15 各输入训练前后隶属度函数变化Fig.15 Membership function change after training

通过两种训练方法的对比可以看出，混合训练方法可以加快模型收敛的速度，降低模型的训练误差，提高模型的估计准确度。

4.3 采用减法聚类方法生成网络的训练

在用减法聚类方法生成网络时，需要设置Range of influence、Squash factor、Accept ratio 和Reject ratio这4个参数的初始值，每个参数的取值范围均由算法要求而定[15]，见表1。

表1 参数取值范围及默认值Tab.1 Parameter ranges and default values

Range of influence的作用是在假定数据点位于一个单位超立方体的条件下，指定数据向量的每一维聚类中心的影响范围，如设置Range of influence为 0.5，则表明数据的聚类中心影响范围为数据空间宽度的1/2。

Squash factor用于与聚类中心的影响范围Range of influence相乘，来决定某一聚类中心附近的哪些数据点被排除作为聚类中心的可能性。

在选出第一个聚类中心后，只有在某个数据点作为聚类中心的可能性值高于第一个聚类中心的可能性值的一定比例时，该数据点才能有作为新的聚类中心的可能性。Accept ratio的作用就是设置这个可能性值的比例。

在选出第一个聚类中心后，只有在某个数据点作为聚类中心的可能性值低于第一个聚类中心的可能性值的一定比例时，该数据点才能排除作为新的聚类中心的可能性。Reject ratio的作用就是设置这个可能性值的比例。

为达到较小的误差，需要不断对这4个参数进行匹配，经过多次训练，可将Range of influence设置为0.4，Squash factor设置为1.0，Accept ratio设置为0.4，Reject ratio设置为0.15，采用减法聚类方式生成的网络模型如图 16所示，从图中可以看出，每个输入语言变量的隶属度函数都有18个，但其节点总数却远远小于网格法生成的网络模型。

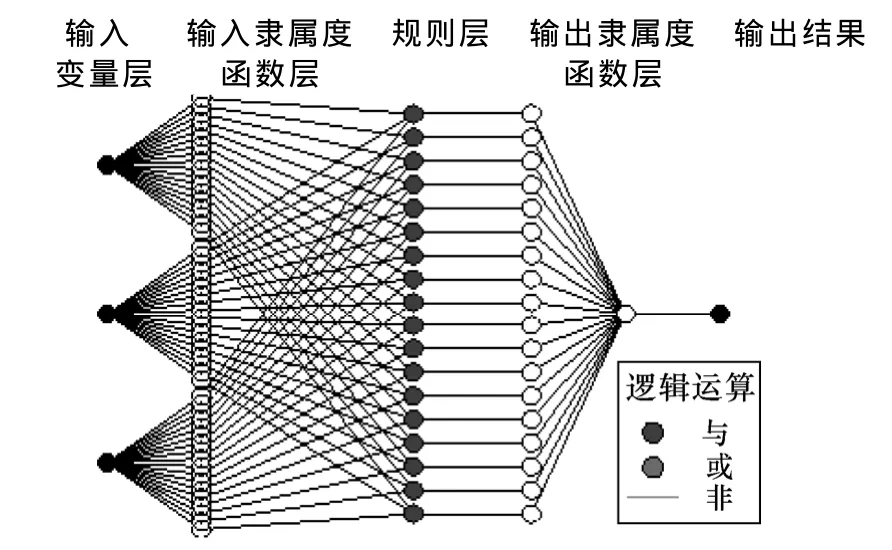
图16 减法聚类法生成的ANFIS模型结构Fig.16 ANFIS model structure generated by subtraction clustering method

混合训练方法的训练误差如图17所示；峰值功率的估计验证如图18所示。其中“*”为模型估计结果，“o”为实际值。

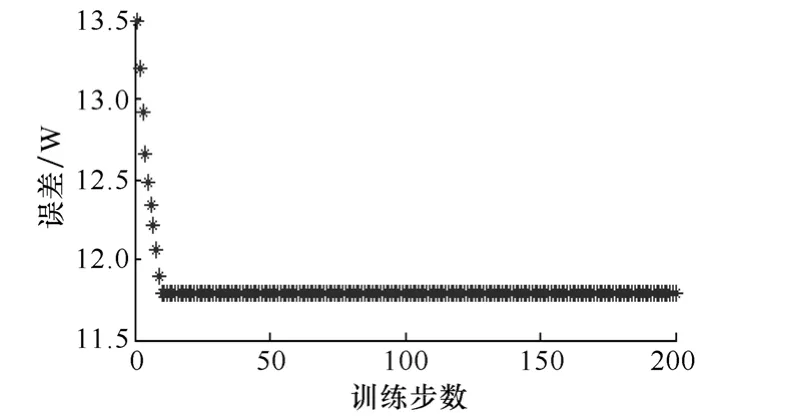
图17 系统训练后误差曲线Fig.17 Error curve after systematic training

图18 模型输出与真实值对比Fig.18 Comparison of model outputs and true values

从图17可看出，系统误差在200步以内便收敛到11.75W，相对误差约为0.7%，从图18也可看出，ANFIS输出值与实际值相比误差比较小。在该误差情况下，训练后的隶属度函数变化如图19所示。从图中可看出隶属度函数数目较多，因此各隶属度函数间重合部分较多，由于欧姆内阻多分布于较小的区间，因此在欧姆内阻较小时，隶属度函数分布较为密集，欧姆内阻较大时，隶属度函数分布很稀疏。

图19 训练后隶属度函数的变化Fig.19 Membership function change after training

4.4 仿真对比

将网格法生成的网络模型和减法聚类法生成的网络模型进行比较，参数对比见表 2。减法聚类在各项参数的简化和模糊规则的优化方面具有非常明显的效果，因此在训练数据巨量的场合，采用减法聚类方法生成的网络模型结构相对简化，同时也节约了训练时间。网格分割的方法将输入模糊空间分别划分4、5、5层，减法聚类的方式却将输入模糊空间划分为18、18、18层，通过训练所得到的误差曲线却表明网格分割法生成的网络训练误差较小，这也说明并不是模糊区间划分越多，模糊规则越多，模型才越准确。

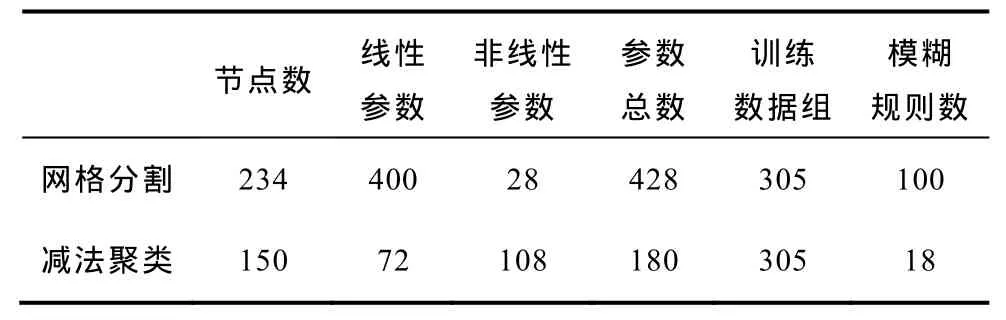
表2 网格法和减法聚类生成网络参数对比Tab.2 Network parameter comparison between grid method and subtractive clustering method

5 基于ANFIS的10s放电峰值功率估计验证

采用同样的测试方法另取125组数据，对ANFIS模型进行验证。通过Simulink仿真，将模型输出与测试的实际值进行比较，比较结果如图20所示，二者相对误差如图21所示。模型输出值与实际测试值相差很小，二者曲线基本吻合，相对误差大部分在10%以内，而且相对误差较大的值多分布在峰值功率低的部分，这是因为低温低 SOC情况下峰值功率值很小，稍有偏差，相对误差便会很大。通过验证发现基于ANFIS的10s放电峰值功率估计方法的估计准确度较高，尤其适用于峰值功率较高的场合。

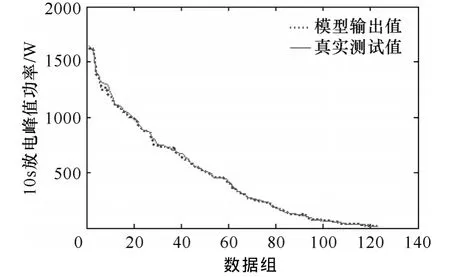
图20 模型输出与真实值对比Fig.20 Comparison of model outputs and true values

图21 模型输出与真实值相对误差Fig.21 The relative errors of model outputs and true values

6 结论

本文针对动力电池应用，提出了一种基于ANFIS的放电峰值功率预测模型。采用减法聚类法生成模糊结构，大幅减少了模糊规则的数目，加快了收敛速度；采用混合训练方法提高了模型的收敛能力并克服了单一 BP算法的局部最优问题，同时提高了准确度。经过仿真验证，模型预测误差在10%以内，表明基于ANFIS的模型能够很好地估计电池的放电峰值功率，而且所用基础数据为电池能够提供的实际峰值功率而非表征值。因此，本方法具有较高的预测准确度和较强的实用价值。

[1] Idaho National Engineering & Environmental Laboratory. Freedom car battery test manual for power-assist hybrid electric vehicles[S]. 2003.

[2] PNGV Battery Test Manual. 2001.

[3] Japan electric vehicle society. Test method of input and output power density of nickel-hydride battery for hybrid electric vehicles[S]. Japan, 2003.

[4] Sun Bingxiang, Wang Lifang, Liao Chenglin. SOC estimation of NiMH battery for HEV based on adaptive neuro-fuzzy inference system[C]. IEEE Vehicle Power and Propulsion Conference, 2008.

[5] 周湶, 孙威, 张昀. 基于改进型 ANFIS的负荷密度指标求取新方法[J]. 电力系统保护与控制, 2011,39(1): 29-34.

Zhou Quan, Sun Wei, Zhang Yun. A new method to obtain load density based on improved ANFIS[J].Power System Protection and Control, 2011, 39(1):29-34.

[6] 张钧, 何正友, 谭熙静. 一种基于 ANFIS的配电网故障分类方法及其适应性分析[J]. 电力系统保护与控制, 2011, 39(4): 23-29.

Zhang Jun, He Zhengyou, Tan Xijing. An ANFIS based fault classification in distribution network and its adaptability analysis[J]. Power System Protection and Control, 2011, 39(4): 23-29.

[7] Zhang Tiejun, Chen Duo, Sun Jie. Research on neural network model based on subtraction clustering and its applications[J]. Physics Procedia, 2012, 25: 1642-1647.

[8] 李培强, 李欣然, 陈辉华, 等. 基于减法聚类的模糊神经网络负荷建模[J]. 电工技术学报, 2006,21(9): 1-6, 12.

Li Peiqiang, Li Xinran, Chen Huihua, et al. Fuzzy neural network load modeling based on subtractive clustering[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 1-6, 12.

[9] 杨茂, 熊昊, 严干贵, 等. 基于数据挖掘和模糊聚类的风电功率实时预测研究[J]. 电力系统保护与控制, 2013, 41(1): 1-6.

Yang Mao, Xiong Hao, Yan Gangui, et al. Real-time prediction of wind power based on data mining and fuzzy clustering[J]. Power System Protection and Control, 2013, 41(1): 1-6.

[10] 白俊良, 梅华威. 改进相似度的模糊聚类算法在光伏阵列短期功率预测中的应用[J]. 电力系统保护与控制, 2014, 42(6): 84-90.

Bai Junliang, Mei Huawei. Improved similarity based fuzzy clustering algorithm and its application in the PV array power short-term forecasting[J]. Power System Protection and Control, 2014, 42(6): 84-90.

[11] 郭宏榆, 姜久春, 王吉松, 等. 功率型锂离子动力电池的内阻特性[J]. 北京交通大学学报, 2011,35(5): 119-123.

Guo Hongyu, Jiang Jiuchun, Wang Jisong, et al.Characteristic on internal resistance of lithiumion power battery[J]. Journal of Beijing Jiaotong University,2011, 35(5): 119-123.

[12] 文锋. 纯电动汽车用锂离子电池组管理技术基础问题研究[D]. 北京: 北京交通大学, 2010.

[13] 杨晟院, 舒适. 一种基于特征线的曲面网格分割方法[J]. 计算机工程与应用, 2008, 44(26): 166-167,182.

Yang Shengyuan, Shu Shi. Method of mesh segmentation based on feature lines[J]. Computer Engineering and Applications, 2008, 44(26): 166-167, 182.

[14] Sun Bingxiang, Wang Lifang. The SOC estimation of NIMH battery pack for HEV based on BP neural network[C]. International Workshop on Intelligent Systems and Applications, 2009.

[15] 范成洲, 曹钧, 王发林, 等. 竖井钻速 ANFIS预测模型训练参数正交试验优化[J]. 矿山机械, 2013(10):108-112.

Fan Chengzhou, Cao Jun, Wang Falin, et al. Optimization on training parameters of shaft-drilled speed prediction model based on ANFIS by orthogonal test[J]. Mining & Processing Equipment, 2013(10):108-112.