变速风力发电系统瞬态载荷分析及其优化设计途径

陈家伟 陈 杰 龚春英

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

面对日益严峻的能源危机和环境污染问题，世界各国都将开发和利用绿色可再生能源作为其可持续发展战略的重要组成部分。风力发电技术，因为政策和技术上的优势，成为了可再生能源发电中发展最为迅速的技术之一[1-4]。

为了最大限度地使风力发电机组（以下简称机组）捕获风能，提高机组的发电效率，通常在额定风速以下需要对机组实施最大功率跟踪控制（Maximum Power Point Tracking，MPPT）。根据现有的文献报道可知，目前关于MPPT 控制的研究重点和热点为提出新型的MPPT 控制策略来提高机组的MPPT 速度，从而最大限度的提高机组捕获的风能。具有代表性的几篇文献报道为：Vivek Agarwal 等在文献[5]中引入MPPT 中间变量因子β 来划分机组的运行区间，通过判断机组所运行的区间而实行相对应的MPPT 控制策略，提高了MPPT 的速度；Ching-Tsai Pan 等在文献[6]中提出了一种气动转矩反馈的控制方法，因气动转矩的引入克服了采用电磁转矩反馈时转动惯量带来的延时，大大提高了机组MPPT 速度；Syed Muhammad Raza Kazmi 等在文献[7]中引入了变步长的扰动观察MPPT 控制方法，在检测到机组工作点远离最大功率点时，控制策略采用较大步长扰动，加快机组接近最大功率点速度；而当机组工作点靠近最大功率点时，则改用较小步长，以减小机组功率脉动，该方法也提高了跟踪的速度。此外，Whei-Min Lin、V.Galdi 等学者将模糊、神经网络等智能算法引入到MPPT 控制策略中，同样旨加快在MPPT 的跟踪速度并提高MPPT 控制的精度[8-14]。

然而，由本文的分析可知，机组MPPT 速度增加的同时，机组传动链上转矩脉动（后文定义为瞬态载荷）也将增大。不仅恶化了机组输出的电能质量，而且使传动链更易疲劳损坏，缩短了机组的服役年限，变相增加了成本。因此，不应一味的追求快的MPPT 速度，还需要对机组承受的瞬态载荷进行优化设计。

本文中以功率反馈MPPT 控制策略为例，通过分析首先找出了 MPPT 速度与瞬态载荷的定量关系。之后，为了优化设计机组承受的瞬态载荷，提出了适用于不同功率等级机组的最大功率跟踪控制系统的跟踪带宽的设计原则。其次，为了使机组可按优化设计的跟踪带宽恒带宽运行，提出了误差功率前馈的控制方法，通过在线调整误差前馈系数，保持了最大功率跟踪带宽的恒定。最后，在实验室内搭建了一台额定功率1.2kW 的永磁直驱变速风力发电机组实验平台，并在此平台上对文中所提出的控制策略进行了实验研究，实验结果验证了本文中理论分析的正确性。

2 MPPT 速度与瞬态载荷关系分析

由空气动力学可知，风力机从风能中捕获的气动功率Pr可按下式计算

式中，ρ为空气密度；R为风轮半径；v为风速；Cp(λ)为风能利用系数，由于本文研究针对机组在低风速区运行状态，风能利用系数只为叶尖速比λ 的函数。

本文中采用的风轮Cp-λ 曲线如图1 中所示，可用式（2）所示多项式进行拟合。

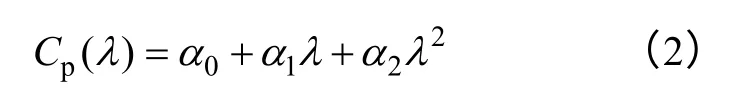
其中α0=-0.312，α1=0.281 4，α2=-0.033 8为拟合系数。

图1 所用风力机Cp-λ曲线Fig.1 Cp-λ curve of the adopted wind turbine

机组叶尖速比λ 与风速v 和机组转速ω 满足关系

对于变速运行的风力发电机组，如果能够根据机组的运行状态实时的改变机组的转速ω，使机组运行的叶尖速比始终保持为最佳值λopt，则风能利用系数可维持为最大值Cpmax，此时机组捕获到最佳功率，表示为

式中，kopt为最佳功率系数。

由上面分析可知，MPPT 实现的过程为调节机组的转速，使机组的功率P 达到最大的过程。在实际机组中，这一过程的实现通常是通过调节电力电子变换器的占空比d 来实现的。因此，可通过求取占空比对机组功率的传递函数∂P/∂d 来获取完成MPPT 所需的时间，即MPPT 速度。

假设机组此时运行于最大点Q（VQ,ωQ,dQ）处，其中VQ、ωQ、dQ分别为该工作点出对应的风速、机组的转速以及工作的占空比信号。在离Q 点很近处的另一点，有

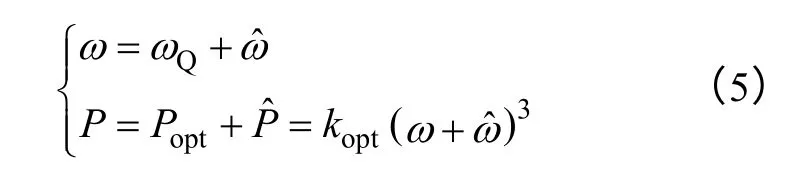
式中，“∧”表示小信号量。

当忽略小信号量的高次方项时，由式（5）可得

对于变速风力发电机组，通常采用机侧整流器对风力发电机组的功率进行控制，而采用后级逆变器控制机组的并网功率（并网机组）或用户用电功率（离网机组）。因此，机组的转速仅受机侧变换器占空比调制，由此可得

因此，由式（6）和式（7）可得

式（8）示出了机组MPPT 运行时的基本关系，对所有的机组类型均适用。为了得出MPPT 速度的定量大小，需要求出式中Gω→d项，而其与机组所采用的结构相关。本文中以一台额定功率为1.2kW 的直驱式变速定桨风力发电机组为例（机组结构如图2中所示，机组参数如表中所示），对MPPT 的速度进行了定量分析。考虑到对于永磁同步发电机，其产生的反电势eω与机组的转速成正比，即满足关系

式中，kω为比例系数。

图2 本文中采用机组结构Fig.2 Adopted wind energy conversion system

表 风力机及永磁发电机参数Tab. Parameters of wind turbine and PMSG

至此，可将图2 中所示的机组结构简化为如图3中所示。其中Vlink为经二极管整流后电压，Vdc为Boost 变换器的输出电压，该电压由后级逆变器控制为稳定，idc为直流侧电流，Rs为PMSG 相绕组电阻，Tr为机组的气动转矩。根据图3 可得

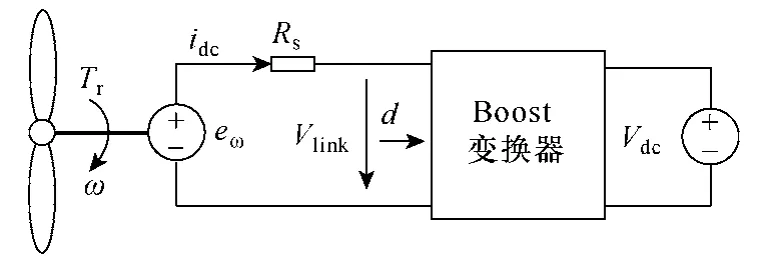
图3 机组简化结构Fig.3 Simplified WECS structure

忽略机组的损耗时，可得发电机的电磁转矩Tg为

因此，可得机组传动链方程为

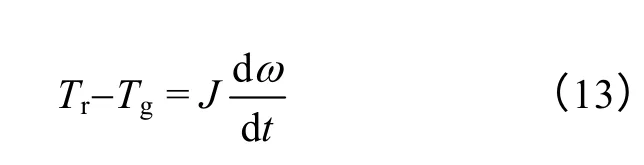
式中，J为机组的总转动惯量，为风轮转动惯量Jr与发电机转动惯量Jg之和；Tr=Pr/ω。

联立式（1）～式（3）及式（12），式（13）可得

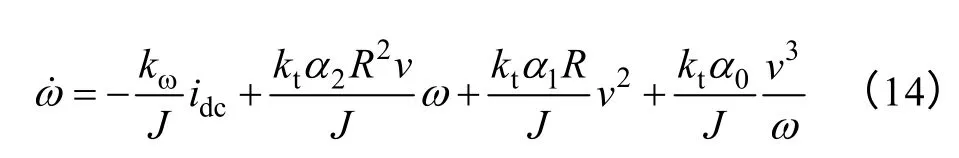
式中，kt=0.5ρπR2。

将式（10）、式（11）代入式（14）并进行线性化分析，可得

上式中系数A、B为

由此可得占空比d 到转速ω 的传递函数

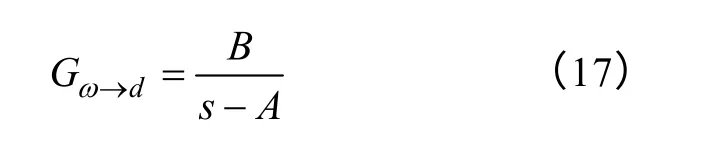
联立式（8）与式（17）可得∂P/∂d 的关系为

运用拉普拉斯反变换，可得由占空比变化引起机组功率变化的动态过程为

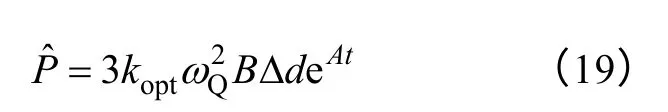
式中

稳态区间ε 通常选为0.1（或更小）。

式（20）示出了因占空比的变化所引起的机组功率变化达到新平衡点所需的时间。风力发电机组常用的MPPT 策略为扰动观察法和基于最佳关系曲线的功率反馈法（后文简称为功率反馈法）[6,15]。当采用扰动观察法时，风速变化过程中控制策略需要经过数次（设为N）上述扰动过程使机组达到新的平衡点，因此MPPT 需要时间可表示为（N·Tε）；而采用功率反馈法时，调节过程中占空比连续变化（不需要达到稳态后进行下一次扰动）直到机组运行到新的稳态点，因此，Tε即为MPPT 所需的时间。考虑到扰动观察法只适用于小型机组，而功率反馈法则适用范围宽，对中大型机组同样适用[16]，后文中讨论时以功率反馈法为例。

对式（20）进行整理，可得功率反馈法的跟踪速度与风速的关系可表示为

对式（1）、式（13）在稳态运行点Q 处进行小信号分析，并线性化可得

由于风速可视为扰动，因此Br=0。而Kr的大小可表示为

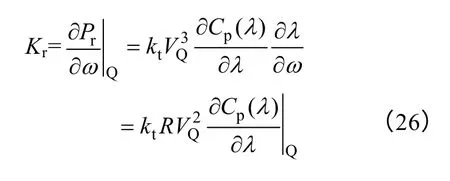
式中，kt=0.5ρπR2。机组运行在最大功率点处时，式（26）中∂Cp(λ)/∂λ=0。因此，联立式（22）、式（25）可得机组MPPT 过程中功率脉动量为

式（27）示出了MPPT 跟踪速度与跟踪过程中机组所承受的功率脉动（定义为瞬态载荷）之间的定量关系。从式中可以看出，MPPT 跟踪速度越快，机组承受的瞬态载荷将越大。过大的瞬态载荷将使机组的传动链更易疲劳损坏。因此，对机组传动链承受的瞬态载荷的优化可通过优化设计机组最大功率跟踪的速度进行来实现。

3 瞬态载荷的优化设计途径

式（27）示出了风速阶跃变化时MPPT 跟踪速度与瞬态载荷的关系式。然而，自然界中的风随时间时刻变化，其变化频率可分布在一个较宽的频带范围内，如图4 中所示的风速的典型范德霍芬频谱[17]。该图中给出了风速中蕴含的能量随着频率分布的关系。从中可看出：①自然界中的风速变化的频率范围宽，可从每小时变化0.001 次至变化500 次以上；②风中蕴含能量较高的风速频率变化可分布为两段：每小时变化次数低于0.2 次的平均风速以及每小时变化次数超过10 次的湍流风速。

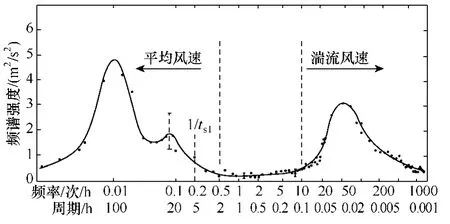
图4 典型的范德霍芬频谱Fig.4 Typical Van Der Hoven spectrum

根据自然界中风速的能量分布以及MPPT 速度与瞬态载荷的关系式（27），可得对机组MPPT 控制系统的设计要求为：

（1）为了提高机组的效率，对湍流风速中蕴含能量较高的湍流风速需要以MPPT 跟踪运行，即不能仅跟踪以0.5 次/h 以下变化的风速。

（2）为了减小机组传动链承受的瞬态载荷MPPT控制系统不应跟踪变化频率过快的湍流风，如大于1 000 次/h。

因此，在设计机组的MPPT 控制系统时，需要合理的布局MPPT 控制系统的响应带宽，从而达到机组的发电效率和承受的瞬态载荷之间的合理平衡。而对于如何优化选取MPPT 系统带宽，目前国内外还没有相关文献报道。本文在此处结合风速的范德霍芬频谱，提出MPPT 控制系统的响应带宽可按如下步骤进行优化选取：

（1）测量机组安装地空气中风动能分布的频域图，也即范德霍芬频谱（风能数据可以从当地的气象部门获得）。之后，根据所得的频谱选取一个合适的跟踪频带范围以保证机组的功率捕获。如在图4所示的频谱中，因以0.01 次/h（4 天一循环）和50次/h（1 分钟一循环）变化的风所含的能量最高，为保证机组的功率捕获，MPPT 系统需要跟踪以这两种频率变化的风速，即跟踪带宽需要高于50 次/h（0.014Hz）。而从图中可知，以1 000 次/h（0.28Hz）及以上频率变化的风速中蕴含的能量很小，如果将最大功率跟踪带宽设置较高，一方面捕获到的风能增加较少，另一方面会增大机组的瞬态载荷。综合考虑，可将系统的带宽初步选取在100 次/h（0.028Hz）与1 000 次/h（0.2Hz）之间。

（2）根据机组的功率等级确定所需要的跟踪带宽。需要考虑两个方面：①对于功率等级为几百千瓦至几兆瓦的中大型机组，因机组的转速通常设计为低速运行（十几转至几十转每分），机组传动链转矩非常大[18,19]。因此，中大型机组考虑的重点应放在如何延长机组的服役年限上。机组MPPT 带宽应设计得较低以获取较小的瞬态载荷。注意到中大型机组通常安装于风能资源较丰富地区，如海上风场，安装地区的风速具有较高的平均风速。因此，对于中大型风力发电机组，本文建议将其MPPT 响应带宽选取为0.001 4～0.027 8Hz。按此原则选取后，不仅机组捕获的功率丢失较少，而且因系统对频率较高的湍流风速不进行MPPT 响应，机组承受的瞬态载荷可相应的减小，有利于机组长期运行；②对于功率等级为一百千瓦以下的中小型风力发电机组（尤其是几百瓦至几千瓦的小型机组），因该类型机组通常用于满足城市（如路灯照明等）以及偏远地区用户的用电需求，机组通常就近用电用户安装，其选址不能得到优化，风能资源可能不足。且中小型风力发电机组额定转速通常设计得相对较高（每分钟几百转），机组传动链转矩较小[20,21]。为了从变化的风速中更可能多的捕获风能，文中建议将MPPT 带宽设计为初选带宽范围的较高值，如0.28Hz。

按照上述原则选取MPPT 系统的带宽后，可使机组承受的瞬态载荷得到优化设计。然而，由后文的分析可知，当MPPT 控制采用常规功率反馈法时，系统的带宽较低，不能满足中小功率场合情况下对跟踪速度要求，特别是在低风速区时，情况更为恶劣。对此，本文将提出一种保证MPPT 系统带宽恒定的方法，从而保证机组的MPPT 性能和承受的瞬态载荷可得到系统化的设计。

4 MPPT 控制系统带宽设计

4.1 常规功率反馈MPPT 系统带宽分析

常规功率反馈MPPT 控制策略的系统实现方法如图5 中所示（不包含虚线框中部分）。该控制策略首先检测机组的运行转速，之后根据式（4）得到机组的最佳功率，通过控制机组的输出功率跟踪该最佳功率从而实现机组的MPPT 运行。

图5 MPPT 控制系统框图Fig.5 System control diagram of MPPT operation

根据上述常规功率反馈 MPPT 策略的基本原理，可知MPPT 运行过程中机组传动链方程可表示为

由于机组的转动惯量大，机组的电气时间常数远小于机械时间常数，因此，可认为机组的输出功率无延时的跟踪了功率基准，即

在稳态工作点Q 处对式（28）、式（29）进行小信号处理，可得机组在常规功率反馈MPPT 方法控制下的动态方程为

式中

同理，当机组运行于最大功率点时，式（31）中(əCp(λ)/əλ)=0。因此可得常规功率反馈MPPT 控制系统的响应带宽为

联立式（3）可得机组的响应带宽的与机组转速和风速的关系为

当机组选定后，式（33）中kopt、λopt、J 以及R均为常数，可知常规功率反馈MPPT 控制系统的响应带宽随着风速的变化成正比变化。对于本文中采用的机组，其MPPT 跟踪的运行范围为6～12m/s，代入机组参数可知对应的 MPPT 系统的带宽为0.133～0.266Hz。而由前文分析可知，对小功率机组，为满足用户的用电需求，MPPT 系统的带宽应选取较高（0.28Hz）以提高机组的功率捕获。然而，常规功率反馈MPPT 系统带宽较低，且随着风速变化而变化，不能满足设计要求。因此，需要对常规功率反馈方法进行改进。

4.2 改进的MPPT 控制策略

为了提高机组的MPPT 速度，且保持机组MPPT系统对风速的变化频率的响应保持不变，实现对MPPT 控制的系统化设计。本文中在常规功率反馈的基础上引入误差功率前馈支路，提出了一种改进的MPPT 方法，如图5 中所示。该方法在机组MPPT跟踪过程中将机组的气动功率与机组当前最佳功率的差值进行前馈，叠加在最佳功率基准上，得到新的功率基准值。如控制机组的输出功率跟踪该功率基准，可拓宽机组MPPT 系统的响应带宽。

加入误差功率前馈后，新的功率基准可表示为

同理，考虑到电气时间常数远小于机械时间常数，即认为机组的输出功率无延时地跟踪上了如式（34）所示的新的功率基准，采用相同的分析方法，可得到改进MPPT 控制系统的带宽为

由式（35）可知，只要前馈系数kf＞0，则采用改进MPPT 控制策略后系统的带宽就高于采用常规功率反馈时的带宽。且可知如果能够根据机组的转速在线调整前馈系数的大小，就可以保证系统带宽的恒定，调整方法为

式中，ωbn为所需的系统带宽。

至此，可根据所需的系统跟踪带宽对机组的MPPT 控制进行系统化的设计，且保证机组的功率捕获和承受的瞬态载荷均得到优化。

此外，可注意到改进的MPPT 策略中需要机组的气动功率。其虽不能直接测量得到，但是可由文献[22]中所提出的气动功率观测器进行观测得出。气动功率观测器的结构框图如图6 中所示，“·obs”为与该变量所对应的观测值，其详细的工作原理见文献[22]。

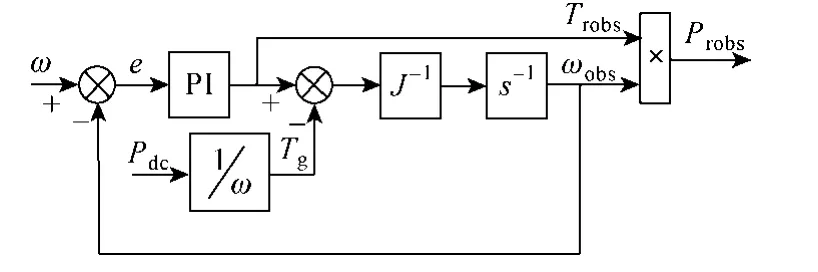
图6 气动功率观测器Fig.6 Aerodynamic power observer

5 仿真实验验证

为了验证前文理论分析的正确性，本文基于Matlab/Simulink 仿真平台和实验室里建立的一台1.2kW 的变速风力发电机组实验平台，对常规功率反馈MPPT 控制策略和文中提出的控制策略进行了仿真和实验对比分析。仿真和试验中，机组结构如图5 中所示，机组参数取值见表。在实验过程中，系统中的真实风力机采用了风力机模拟系统来代替，不仅方便了在实验室中进行系统实验，而且可以方便地模拟各种复杂风况。风力机模拟系统的工作原理和正确性在前期的研究中已经进行了详细分析和验证，这里不再详述，请参见文献[23]。

图7 所示为风速由7m/s 阶跃到10m/s，之后再由10m/s 阶跃为7m/s 情况下，机组转速、电磁转矩以及风能利用系数Cp变化过程的仿真和实验结果。从图中可以看出，在风速变化过程中，采用常规功率反馈MPPT 策略时系统需要约2.2s 时间才能重新追踪到新的最大功率点运行，这与式（22）的计算结果相近（代入机组参数可计算）。采用改进的MPPT 策略后，跟踪过程缩短至1.3s，MPPT 的速度加快。然而，可注意到在动态过程中，MPPT 速度的增加带来了更大的转矩脉动，如在风速增加时发电机转矩减小，在风速降低时发电机转矩增大。说明 MPPT 速度的增加是靠增加传动链的转矩脉动，即瞬态载荷来实现的，这与前文的理论分析一致。

为了验证文中控制系统带宽分析的正确性，文中采用正弦型风速来测试常规MPPT 控制策略和文中提出的改进型MPPT 控制策略的跟踪带宽，采用的风速形式为

上式所述风速为：平均风速8.5m/s，之上叠加频率为0.04Hz 和频率为0.2Hz 变化的风速。

在式（37）所示的风速作用下，机组风能利用系数Cp、转速及电磁转矩变化过程仿真及实验结果如图8 所示。从图中可以看出，当机组采用常规功率反馈MPPT 控制时，在风速最低点处，风能利用系数Cp值下掉较多，随着风速的增加，Cp值掉落减小，且当风速达到8.5m/s 以上时，Cp值几乎无掉落。造成该现象的原因为：根据式（33），常规功率反馈MPPT 控制系统的带宽随着风速变化而变化。图8 中风速变化范围约为6～11m/s，由式（33）可计算出系统的响应带宽变化范围为0.133～0.243Hz，且在8.5m/s 时系统带宽为0.2Hz。

图7 机组在阶跃型风速下关键参数仿真及实验曲线Fig.7 Simulation and experimental waveforms of some key parameters of the turbine under step-type wind speed

当风速小于8.5m/s 时，MPPT 系统响应带宽不足，系统对0.2Hz 变化的风速不进行MPPT 响应，造成Cp掉落。而在高风速时系统带宽大于风速变化频率，因此机组可追踪上0.2Hz 变化的风速。而采用文中所提出的改进MPPT 控制策略后，在风速变化时因系统的带宽根据需要可固定为0.28Hz，从图8 中可以看出，对于0.2Hz 频率变化的风速，不管高风速段还是低风速段，风能利用系数始终维持在最大值附近。说明采用改进的MPPT 控制方法后，系统的带宽可设计为恒定。至此，机组MPPT系统的带宽可根据本文第2 节中的要求实现按需设计。

6 结论

本文首先详细分析了机组MPPT 跟踪过程中跟踪速度与传动链承受的瞬态载荷的关系，指出跟踪速度越快，瞬态载荷将越大。其次，为了优化机组的瞬态载荷，对MPPT 系统的带宽进行了合理的设计，保证了机组不对快速变化的风速进行MPPT 响应，从而减小机组承受的瞬态载荷。之后，为了使机组可按照优化选取的带宽恒带宽运行，提出了一种改进的MPPT 策略，通过实验验证了其正确性和可行性。

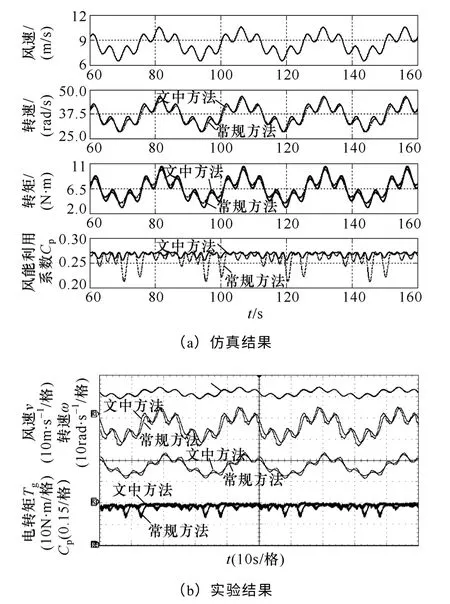
图8 机组在正弦型风速下关键参数仿真及实验曲线Fig.8 Simulation and experimental waveforms of some key parameters of the turbine under sine-type wind speed

[1]Li H,Chen Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2)：123-128.

[2]郭金东,赵栋利,林资旭,等.兆瓦级变速恒频风力发电机组控制系统[J].中国电机工程学报,2007,27(2)：1-5.Guo Jindong,Zhao Dongli,Lin Zixu,et al.Research of the megawatt level variable speed constant frequency wind power unit control system[J].Proceedings of the CSEE,2007,27(2)：1-5.

[3]American Wind Energy Association(AWEA).AWEA small wind global market study 2010.http：//www.awea.org.

[4]Bang D,Polinder H,Shrestha G,et al.Review of generator systems for direct-drive wind turbines[C].European Wind Energy Conference and Exhibition,Belgium,Brussels,2008.

[5]Agarwal V,Aggarwal R K,Patidar Pravin,et al.A novel scheme for rapid tracking of maximum power point in wind energy generation systems[J].IEEE Transactions on Energy Conversion,2010,25(1)：228-236.

[6]Pan Ching Tsai,Juan Yuling.A novel sensorless MPPT controller for a high-efficiency micro-scale wind power generation system[J].IEEE Transactions on Energy Conversion,2010,25(1)：207-216.

[7]Kazmi S M R,Goto H,Guo Haijiao,et al.A novel algorithm for fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems[J].IEEE Transactions on Energy Conversion,2011,58(1)：29-36.

[8]Lin Whei Min,Hong Chih Ming.Intelligent approach to maximum power point tracking control strategy for variable-speed wind turbine generation system[J].Energy,2010(35)：2440-2447.

[9]Galdi V,Piccolo A,Siano P.Exploiting maximum energy from variable speed wind power generation systems by using an adaptive Takagi–Sugeno–Kang fuzzy model[J].Energy Conversion and Management,2009(50)：413-421.

[10]Beltran Brice,Tarek Ahmed-Ali,Mohamed Benbouzid.Sliding mode power control of variable-speed wind energy conversion systems[J].IEEE Transaction on Energy Conversion,2008,23(2)：551-558.

[11]K Ying Shieh,T Ming Hung.FPGA-based speed control IC for PMSM drive with Adaptive fuzzy control[J].IEEE Transactions on Power Electronics,2007,22(6)：2476-2486.

[12]陈杰,陈冉,陈家伟,等.变速风力发电机组的模糊-单神经元PID 控制[J].中国电机工程学报,2011,31(27)：88-94.Chen Jie,Chen Ran,Chen Jiawei,et al.Fuzzy singleneuron PID control of variable speed wind turbines[J].Proceedings of the CSEE,2011,31(27)：88-94.

[13]A Kusiak,Zhang Zijun.Adaptive control of a wind turbine with data mining and swarm intelligence[J].IEEE Transactions on Sustainable Energy,2011,2(1)：28-36.

[14]Masiala M,Vafakhah B,Salmon J,et al.Fuzzy self-tuning speed control of an indirect field-oriented control induction motor drive[J].IEEE Transaction on Industry Applications,2008,44(6)：1732-1740.

[15]赵仁德,王永军,张加胜.直驱式永磁同步风力发电系统最大功率追踪控制[J].中国电机工程学报,2009,29(27)：106-111.Zhao Rende,Wang Yongjun,Zhang Jiasheng.Maximum power point tracking control of the wind energy generation system with direct-driven permanent magnet synchronous generators[J].Proceedings of the CSEE,2005,2009,29(27)：106-111.

[16]Haque M E,Negnevitsky M,Muttaqi K M.A novel control strategy for a variable-speed wind turbine with a permanent-magnet synchronous generator[J].IEEE Transaction on Industrial Applications,2010,46(1)：331-339.

[17]Bianchi Fernando D,Battista Hernan De,Mantz Ricardo J.Wind turbine control systems principles,modeling and gain scheduling design[M].Advances in Industrial Control Series,2006.

[18]李晶,宋佳骅,王伟胜.大型变速恒频风力发电机组建模与仿真[J].中国电机工程学报,2004,24(6)：100-105.Li Jing,Song Jiahua,Wang Weisheng.Modeling and dynamic simulation of variable-speed wind turbine with large capacity[J].Proceedings of the CSEE,2004,24(6)：100-105.

[19]Geng Hua,Yang Geng,Xu David,et al.Unified power control for PMSG-based WECS operatingunder different grid conditions[J].IEEE Transaction on Energy Conversion,2011,26(3)：822-830.

[20]Ciprian Vlad,Iulian Munteanu,Antoneta Iuliana Bratcu,et al.Output power maximization of lowpower wind energy conversion systems revisited：possible control solutions[J].Energy Conversion and Management,2010,51：305-310.

[21]Ani Samuel,Polinder Henk,Ferreira Braham.Comparison of energy yield of small wind turbines in low wind speed area[J].IEEE Transactions on Sustainable Energy,Early Access Articles 2012.

[22]Rolf Hoffmann.A comparison of control concepts for wind turbines in terms of energy capture[D].Darmstadt：Darmstadt University of Technology,2002.

[23]陈杰,陈家伟,陈冉,等.基于永磁同步电机的风力机动静态特性模拟[J].中国电机工程学报,2011,31(15)：40-46.Chen Jie,Chen Jiawei,Chen Ran,et al.Static and dynamic behavior simulation of wind turbine based on PMSM[J].Proceedings of the CSEE,2011,31(15)：40-46.