基于模块化多电平变换器的电流滞环跟踪型并网控制策略

吉 宇 梅 军 杜晓舟 韩少华 郑建勇

（东南大学电气工程学院 南京 210096）

1 引言

模块化多电平变换器（Modular Multilevel Converter，MMC）是近年出现的一种新型电压源变换器拓扑结构，是多电平变换器拓扑结构的一个重大突破。其最早由慕尼黑联邦国防军大学的Marquardt和Lesnicar 等人提出，主要适用于高电压等级、大容量的有功变换的场合。和级联H 桥变流器相比，MMC 保留了高度模块化的结构特点，同时又具有一个高压直流母线，能够实现输出电压、输出电流的四象限运行。和传统的二、三电平变流器相比，MMC 不存在开关管串联并联的均压、均流的问题。MMC 的每个子模块结构相对简单，控制容易，可以无限扩展，特别适用于HVDC 领域。西门子“Trans Bay Cable”工程是世界上第一个基于MMC 变换器的直流输电工程（MMC-HVDC），于2010年11 月在美国旧金山市北部投入运行，该工程的设计容量为400MW，额定电压为±200kV，单个桥臂由200个子模块构成[1-6]。

国内对MMC 的研究起步虽更晚，但研究比较活跃，中国电力科学研究院、华北电力大学、浙江大学和合肥工业大学等单位已经开展了这方面的基础理论研究，研究工作主要集中在MMC-HVDC 的建模仿真，MMC-HVDC 的控制和保护策略等。上海供电公司和中国电力科学研究院合作的上海南汇风电场示范工程是我国第一个MMC 工程，于2011年7 月25 日正式投入运行[1-3]。

MMC 并网逆变器主要控制问题是输出电流能够实时跟踪电网的相位、频率，而且电流的总畸变失真要低，从而减少对电网的谐波影响[1-5]。

电流跟踪型PWM 逆变器具有实时控制输出电流、快速响应等特点，主要分为三角载波调制、滞环调制两种方式。目前，应用在MMC 中的电流跟踪型PWM 逆变器一般采用三角载波调制法，这种方法的开关频率固定，但响应速度较慢。而且采用三角载波调制的并网逆变器需要进行有功和无功的解耦控制，相对比较复杂，鲁棒性较差。

本文针对 MMC 并网逆变器运行特点进行研究，提出了一种基于虚拟循环映射的电流滞环型MMC 双闭环并网控制策略，实现了并网电流脉动频率降低、开关频率降低、所有子模块悬浮电容电压平衡。该并网控制策略在一台五电平MMC 样机上得到了实验验证[6,7]。

2 拓扑结构和工作原理

图1为n+1 电平三相MMC 的拓扑结构以及子模块结构，它由6 个桥臂构成。其中，每一个桥臂都由n 个子模块和电抗器L 串联构成，电抗器L起到限流作用，上、下两个桥臂构成了MMC 的一相。

MMC 的三相6 个桥臂具有对称性，其电气参数和电抗值都是相同的。这里以a 相为例，直流侧正、负母线相对于中点 o 的电压分别为 0.5Udc、-0.5Udc。Uap、Uan分别为a 相上、下桥臂子模块输出电压之和，Iap、Ian分别为a 相上、下桥臂的桥臂电流，Ia为a 相的网侧电流，可以得到

图1 三相MMC 拓扑结构图Fig.1 Three-phase equivalent circuit of MMC

结合式（1）～式（3）可得

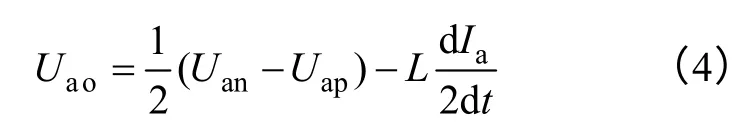
MMC 子模块是一个半桥结构，包括两个IGBT和一个直流储能电容。根据电流ISM的方向以及开关S1和S2的状态，子模块的输出电压在UC和0 之间切换。具体的开关状态由表1 可见，其中“1”代表开关导通，“0”代表开关关断[4,5]。

表1 MMC 子模块工作状态Tab.1 MMC submodule working states

3 电流滞环型逆变器控制原理

3.1 逆变器并网控制系统

MMC 并网逆变器采用电压外环、电流控制内环的双闭环控制策略。首先通过Park 变换将三相静止坐标系的变量转换为两相同步旋转坐标系，同时将d 轴定义成电网电压矢量的方向。在这样的定义下，实时监测的MMC 逆变器直流侧母线电压Udc和向电网输出的有功功率P、无功功率Q。并网逆变器向电网输出的有功功率P、无功功率Q 表示为

图2为MMC 并网逆变器双闭环控制系统框图。通过对直流侧母线电压误差的PI 控制，得到有功电流给定值Id_ref，而通过对无功误差的PI 控制，得到无功电流给定值Iq_ref。得到有功、无功电流参考值后进行Park 反变换得到三相的电流给定值，采用电流滞环调制法进行实时跟踪给定值，实现母线电压稳定和功率因数的控制。和基于三角载波PI 调制的电流内环相比，电流滞环调制的电流内环速度更快、精度更高、鲁棒性更强，具有快速的动态响应和自动的峰值限制能力，而且不存在d、q 轴解耦问题，具有明显的优势。当直流侧电压一定的情况下，子模块数越多，则每个子模块电容电压越小，开关管电压应力越小，可以选择频率相对高的开关管。同时，MMC 采用多电平调制，和二电平、三电平逆变器相比，MMC 每个子模块开关动作频率要求相对比较低，相对更适用电流滞环调制[3]。

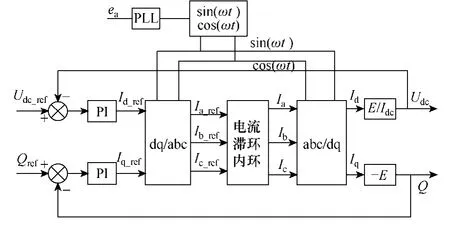
图2 MMC 并网逆变器双闭环控制系统框图Fig.2 Double closed-loop control strategy for grid connected modular multilevel converter

当然，电流滞环调制也有缺点，其开关频率是变化的，这对逆变器开关管来说是有一定制约的[8-10]。

3.2 电流滞环控制

电流滞环型内环用来控制MMC 并网逆变器的并网电流，实现对得到的电流给定值实时跟踪，响应速度快，而且稳定性好。同样以a 相为例，按照图1 的物理量符号含义及方向可以得到

由于三相完全对称，则有

结合式（4）、式（7）和式（8），可得

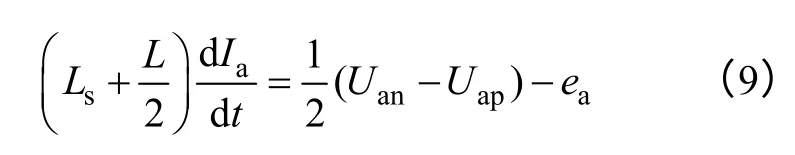
简化式（9），可得

式中，La为a 相的等效电抗；Udao为a 相的等效输出电压；UAO为a 相的等效输出电压与电网电压的差值，单相等效并网电路如图3 所示[11-14]。

图3 单相等效并网原理图Fig.3 Single-phase equivalent circuit of grid connected modular multilevel converter

图4 电流滞环控制原理图Fig.4 Principle drawing of hysteresis-band current tracking control

电流滞环控制原理如图4 所示，将输出反馈电流和参考电流的误差与滞环阈值h 进行比较。构建函数D(t)，当误差超过滞环的上阈值时，令D(t)=0，需要电感电流有下降的趋势，则UAo＜0，使得误差减小。当误差超过滞环的下阈值时，令D(t)=1，需要电感电流有上升的趋势，则UAo＞0，使得误差减小。另外，当误差在滞环内时，D(t)不变[3,4]。

显然，输出并网电流在一个开关周期内律动一次，设电流上升时间和下降时间分别为T1和T2，电流上升时间MMC 的等效输出电压为Udao1，电流下降时间MMC 的等效输出电压为Udao2，电流变化的环宽为h，在足够高的开关频率下，由式（10）可得

输出并网电流脉动周期T为

输出并网电流脉动频率为

构建函数V(t)，用来对电网电压ea(t)的大小和相位进行分区间，有

结合之前的分析，当电网电压ea(t)处在m 区间（V(t)=m）时，若误差超过滞环的上阈值时（D(t)=0），MMC 等效输出电压Udao2=(m-1)USM-Udc2。若当误差超过滞环的下阈值时（D(t)=1），等效输出电压Udao1=mUSM-Udc2。若当误差在滞环内时，等效输出电压Udao不变。总之，每个时刻MMC 等效输出电压为

即每个时刻，MMC 下桥臂投入模块数

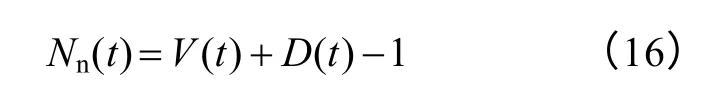
结合式（13），可得

当ea(t)=Udao2(t)+USM2时，输出并网电流脉动取最大频率为

根据式（18），并网电流脉动最大频率和上、下桥臂模块数成反比。当母线电压一定，其他参数不变时，只要上/下桥臂子模块数n 越大，则输出并网电流脉动最大频率越小，相应地，开关管频率越小。可见，相对于两电平电流滞环型逆变器，MMC 电流滞环在开关频率上有很大优势[3]。

3.3 n+1 电平调制

结合之前的分析，为了保持直流侧电压稳定，减少其纹波，这里采用n+1 电平调制法。可以得到每个时刻下桥臂投入的模块数Nn(t)、上桥臂投入的模块数Np(t)存在以下关系

式中，0≤V(t)≤n；D(t)=0 或1；1≤Nn(t)≤n；1≤Np(t)≤n。n为上/下桥臂的子模块数。在系统对称运行的情况下，为了平衡子模块电容电压，必须保持上/下桥臂中各子模块投入或切除的概率相等，这就需要引入虚拟循环映射。

建立虚拟子模块（VSM），其数目和实际子模块（RSM）数目相同，编号分别为1′～2n′。实时计算出的Np(t)、Nn(t)首先传递到虚拟子模块，使得虚拟子模块1′～n′投入的总数为Np(t)，而虚拟子模块(n+1)′～2n′投入的总数为Nn(t)。

另外，定义上桥臂虚拟子模块1′投入的概率大于虚拟子模块2′投入的概率，虚拟子模块2′投入的概率大于虚拟子模块3′投入的概率，以此类推，虚拟子模块1′投入的概率是最大的，而虚拟子模块n′投入的概率是最小的。同时，下桥臂虚拟子模块(n+1)′～2n′的投入情况分别和1′～n′相反。

为了简便，假设上/下桥臂的实际子模块数都是4(n=4)，则需要建立8 个虚拟子模块，标号分别为1′～8′，具体的虚拟子模块调制信号真值见表2。

表2 虚拟子模块调制信号真值表Tab.2 Switch combinations of VSM

如表2 所示，1′～4′是代表上桥臂的虚拟子模块，而5′～8′是代表下桥臂的虚拟子模块。这里，“1”代表投入，“0”则代表切除[15]。

虚拟子模块必须映射到实际子模块中去，其映射关系将在下节详细描述。

3.4 虚拟循环映射

为了保证MMC 系统长期稳定运行，必须保证各个子模块电容电压的平衡。有两个方法能够解决电容电压平衡的问题：虚拟循环映射和基于子模块电容电压大小比较、桥臂电流方向的改进型虚拟循环映射。前者控制方法相对简单，一般使用于变换器在对称运行的情况下。后者相对比较复杂，但功能性更强，适用于变换器在不对称运行的情况下。

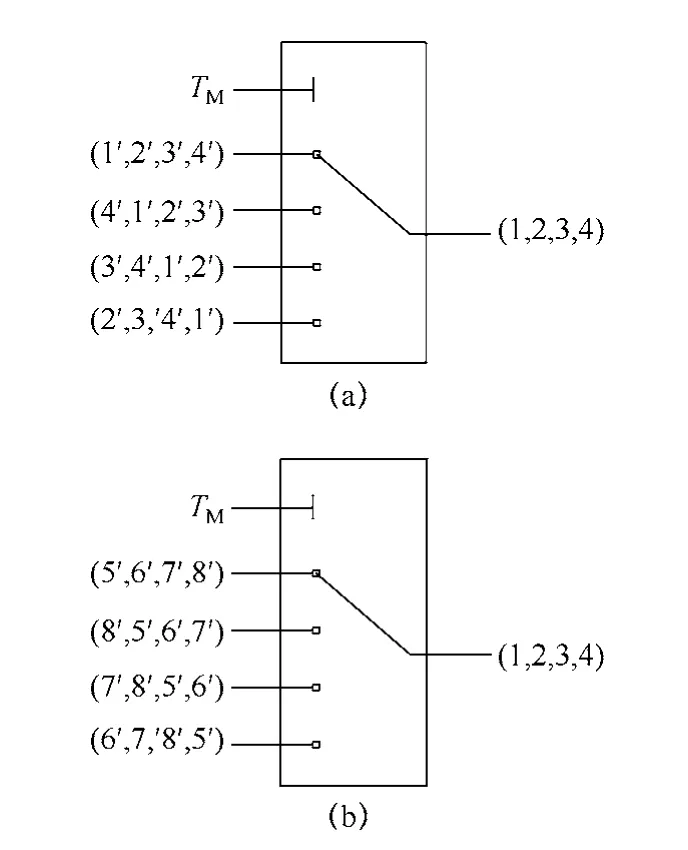
图5 虚拟循环映射（n=4）Fig.5 Loop mapping relationships between the VSMs and RSMs

图5a为上桥臂虚拟子模块和实际子模块的映射关系，而图5b为下桥臂虚拟子模块和实际子模块的映射关系。举个例子，若TM=1，则虚拟子模块1′-2′-3′-4′将分别映射到实际子模块1-2-3-4，而5′-6′-7′-8′将分别映射到5-6-7-8。若TM=2，则虚拟子模块 4′-1′-2′-3′将分别映射到实际子模块1-2-3-4，而8′-5′-6′-7′将分别映射到5-6-7-8，以此类推，可得到虚拟循环映射的实际结果图，如图6所示。

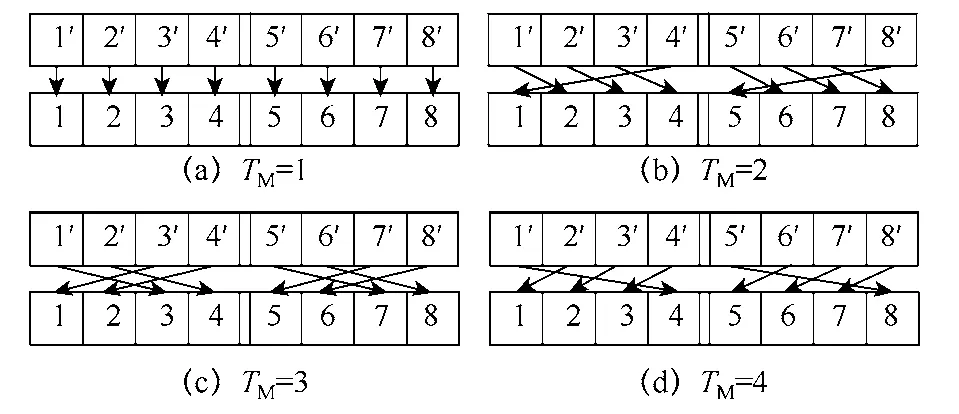
图6 虚拟循环映射结果（n=4）Fig.6 Final results of loop mapping relationships

3.5 基于改进型虚拟循环映射的子模块电容电压平衡控制策略

当变换器处在不对称运行的状态下，各子模块失去平衡，如果还是采用虚拟循环映射不可能使得子模块电容电压趋于平衡，必须对此策略加以改进，引入改进型虚拟循环映射，使失衡的子模块尽快恢复正常，变换器回到对称运行。

改进型虚拟循环映射的策略如下：定时找出电容电压失衡最严重的两个子模块，其中一个是电容电压值最大的子模块，一个是电容电压值最小的子模块。对电容电压值最大的子模块实现“多放电”、“少充电”，对电容电压值最小的子模块则实现“少放电”、“多充电”。

系统定时对上、下桥臂各个子模块电容电压进行了比较，同时实时监测上、下桥臂的桥臂电流方向，这些都可以在AD 采样芯片和FPGA 中完成。以上桥臂为例，假设T1时刻，找出最大电容电压值子模块的序号为1，而最小电容电压值子模块的序号为2。在此同时，实时监测上桥臂的桥臂电流Ip方向。若Ip≥0，说明上桥臂处在充电状态，故实际子模块1 在此周期内得少充电，映射到投入概率最小的虚拟子模块4′；实际子模块2 得多充电，映射到投入概率最大的虚拟子模块1′。若Ip＜0，说明上桥臂处在放电状态，故实际子模块1 得多放电，映射到虚拟子模块1′；实际子模块2 得少放电，映射到虚拟子模块4′。从而得到具体的改进型虚拟循环映射实际结果图，如图7 所示。

图7 改进型虚拟循环映射结果（n=4）Fig.7 Final results of improved loop mapping relationships

图7a 和图7b 代表的是桥臂电流Ip≥0 的情况，而图7c、图7d 代表的是桥臂电流Ip＜0 的情况。可见虚拟子模块1′、4′（1′、n′）是固定映射到两个实际子模块，而另外的两个虚拟子模块和两个实际子模块是循环映射的，这里和虚拟循环映射是一致的。

如图7 所示，以电容电压最大的子模块1为例。当Ip≥0 时，子模块1 映射到虚拟子模块4′。结合表2，若Np(t)=0～3，子模块1 都切除，不参加充电，而其他上桥臂子模块投入充电；若Np(t)=4，子模块1 和上桥臂其他子模块都投入充电。当Ip＜0 时，子模块1 映射到虚拟子模块1′。若Np(t)=0～3，子模块1 都投入，参加放电，而其他子模块可能在切除状态；若Np(t)=4，子模块1 和上桥臂其他子模块都切除。在此周期中，子模块1 相比其他子模块，在Ip≥0 时，充电时间相对短。在Ip＜0 时，放电时间相对长。经过一个周期，原先电容电压最大的子模块1 中的电容电压下降。同理，一个周期后，原先电容电压最小的子模块2 中的电容电压上升。

当然，该桥臂中电容电压值最大、最小的子模块不可能是一成不变的，故在下一个采样周期，再次判断电容电压最大值、最小值的实际子模块序号，重复之前的步骤。同理，下桥臂的控制策略和上桥臂完全相同。经过一段时间后，每个桥臂中子模块电容电压都将趋于相等，MMC 系统也将回到对称平衡的运行模式。

对于学时安排，调查中有78名（21.61%）学生认为理论课授课速度较快，272名（75.35%）学生认为适宜，11名（3.05%）学生认为较慢；调查中有135名（37.40%）学生认为实践课对学习理论知识帮助很大，210名（58.17%）学生认为有一定帮助，16名（4.43%）学生认为没有帮助或不清楚有无帮助。

基于改进型虚拟循环映射的子模块电容电压平衡策略相对虚拟循环映射策略而言，实现起来比较复杂，占用更多的硬件资源。然而，在工程实际中，此方法具有强大的纠错功能，能够更好地实现子模块电容电压动态平衡，优势相当明显。

4 仿真和实验分析

4.1 仿真与分析

利用Matlab/Simulink 分别对单相五电平、九电平MMC 电流滞环并网系统进行了仿真。仿真参数如下：直流母线电压 800V，输出交流电压峰峰值622V，频率为50Hz，输出滤波电感8mH，桥臂电感2mH，子模块电容容值2 200μF。给定电流峰峰值为7A，环宽h=0.02A，仿真结果如图8 所示。

图8 仿真波形Fig.8 The simulation waveforms

图8a 和图8c 分别为五电平、九电平系统电网电压、MMC 系统输出电压和输出电流的仿真波形，可以看到并网电流和电网电压相位、频率都完全一致，实现系统功率因数为1。图8b 和图8d 分别为五电平、九电平系统MMC 系统子模块的电容电压。五电平系统子模块电容电压在200V 左右波动，九电平系统子模块电容电压在100V 左右波动，子模块电容电压是平衡的。可见，子模块数越多，则电平数越多，子模块电容电压越小。

此种电流滞环型并网控制策略适用于任意模块数的MMC 变换器，具有很强的扩展性与应用性。

4.2 实验结果

设计以dsp28335+FPGA为控制核心的单相五电平MMC 电流滞环型并网系统。样机参数：直流母线输入电压400V，桥臂电感1.5mH，子模块电容容值2 200μF，网侧电感8mH，输出交流侧通过变压器进行并网。在此条件下，对MMC 系统进行了实验研究。根据式（18）可见，并网电流脉动频率和环宽成反比，环宽h 越小，则并网电流越精确快速地跟踪指令电流，但开关频率也越大。综合考虑，实验取环宽h=0.02A，具体实验结果如图9所示。

图9 实验波形Fig.9 The experimental waveforms

图9 中，图9a 从上往下依次为输出电压、网侧电流波形以及上下桥臂的桥臂电流波形，图9b为输出电压、网侧电流波形，图9c为输出电压和实际子模块开关管驱动波形。

图9a 可见，正常工作时上、下桥臂的桥臂电流峰峰值为5A，其差值即为MMC 变换器输出的并网电流。

图9b 可见，输出并网电流和输出电压同相位，其峰峰值为6A，能够精确、快速地跟踪给定电流，且正弦度很高。相比二电平或三电平的并网逆变器，其输出并网电流脉动频率相对比较低。另外，相比三角载波调制策略，电流滞环调制策略具有快速的动态响应和自动的峰值限制能力[3]。

图9c 可见，当MMC 变换器稳定运行时，子模块开关管的动作频率是周期性的、稳定的，其动作频率主要取决于输出并网电流脉动频率以及虚拟循环映射的计数器频率。

此外，图9 可见，输出电压波形相当稳定，相邻电平的电压差稳定在100V 左右，说明子模块电容电压保持平衡，该并网系统可以长期稳定运行。

图10 实验样机Fig.10 The experimental prototype of MMC

5 结论

MMC 在高电压大容量场合有着非常广泛的应用前景，本文提出了一种适用于MMC 的电流滞环型双闭环并网控制策略，实现了并网输出电流快速、高效地跟踪给定电流。另外，详细描写并比较了虚拟循环映射控制策略、改进型虚拟循环映射控制策略，实现了所有悬浮电容电压的动态平衡控制。这种方法适用于任意电平数和模块单元数，便于扩展，可以很好地应用到实际工程[15-17]。

[1]杨晓峰,郑琼林.基于MMC 环流模型的通用环流抑制策略[J].中国电机工程学报,2012,32(18)：59-65.Yang Xiaofeng,Zheng Qionglin.A novel universal circulating current suppressing strategy based on the MMC circulating current model[J].Proceedings of the CSEE,2012,32(18)：59-65.

[2]王奎,郑泽东,李永东.基于新型模块化多电平变换器五电平PWM 整流器[J].电工技术学报,2011,26(5)：34-38.Wang Kui,Zheng Zedong,Li Yongdong.A five-level PWM rectifier based on new modular multilevel converter[J].Transactions of China Electrotechnical Society,2011,26(5)：34-38.

[3]顾和荣,杨子龙,邬伟扬.并网逆变器输出电流滞环跟踪控制技术研究[J].中国电机工程学报,2006,26(9)：108-112.Gu Herong,Yang Zilong,Wu Weiyang.Research on hysteresis-band current tracking control of gridconnected inverter[J].Proceedings of the CSEE,2006,26(9)：108-112.

[4]洪峰,单任仲,王慧贞,等.一种变环宽准恒频电流滞环控制方法[J].电工技术学报,2009,24(1)：115-119.Hong Feng,Shan Renzhong,Wang Huizhen,et al.A Varied hysteresis-band current controller with fixed switching frequency[J].Transactions of China Electrotechnical Society,2009,24(1)：115-119.

[5]Guan M,Xu Z.Modeling and control of a modular multilevel converter-based HVDC system under unbalanced grid conditions[J].IEEE Transactions on Power Electronics,2012,27(12)：4858-4867.

[6]Jun Mei,Bailu Xiao,Ke Shen.Modular multilevel inverter with new modulation method and its application to photovoltaic grid-connected generator[J].IEEE Transactions on Power Electronics,2013,28(11)：5063-5073.

[7]Du C,Agneholm E,Olsson G.VSC-HVDC system for industrial plants with onsite generators[J].IEEE Transactions on Power Delivery,2009,24(3)：1359-1366.

[8]Lesnicar A,Marquardt R.An innovative modular multilevel converter topology suitable for a wide power range[C].Proceedings of IEEE Power Tech Conference,2003,1：1-6.

[9]朱劲松,李磊.基于模块化多电平换流器的STATCOM 分析与控制[J].电力系统保护与控制,2012,40(24)：113-117.Zhu Jinsong,Li Lei.Analysis and control of STATCOM based on modular multilevel converters[J].Power System Protection and Control,2012,40(24)：113-117.

[10]Mohammadi H P,Bina M T H.A transformerless medium-voltage STATCOM topology based on extended modular multilevel converters[J].IEEE Transactions on Power Electronics,2011,26(5)：1534-1545.

[11]Alajmi B N,Ahmed K H,Adam G P,et al.Modular multilevel inverter with maximum power point tracking for grid connected photovoltaic application[J].IEEE International Symposium on Industrial Electronics,2011,22(6)：2057-2062.

[12]饶建业,李永东.一种混合级联型多电平逆变器拓扑结构[J].电工技术学报,2009,24(3)：104-109.Rao Jianye,Li Yongdong.Investigation of control method for a hybrid cascaded multilevel inverter[J].Transactions of China Electrotechnical Society,2009,24(3)：104-109.

[13]Rajasekar S,Gupta R.Solar photovoltaic power conversion using modular multilevel converter[J].Students Conference on Engineering and Systems,2012,1(1)：1-6.

[14]翟晓萌,赵成勇,李路遥,等.模块化多电平动态电压恢复器的研究[J].电力系统保护与控制,2013,41(12)：86-91.Zhai Xiaomeng,Zhao Chengyong,Li Luyao,et al.Study of modular multilevel dynamic voltage restorer[J].Power System Protection and Control,2013,41(12)：86-91.

[15]Hagiwara M,Maeda R,Akagi H.Control and analysis of the modular multilevel cascade converter based ondouble-star chopper-cells[J].IEEE Transactions on Power Electronics,2011,26(6)：1649-1658.

[16]丁冠军,丁明,汤广福,等.新型多电平VSC 子模块电容参数与均压策略[J].中国电机工程学报,2009,29(30)：1-6.Ding Guanjun,Ding Ming,Tang Guangfu,et al.Submodule capacitance parameter and voltage balancing scheme of a new multilevel VSC[J].Proceedings of the CSEE,2009,29(30)：1-6.

[17]连霄壤,江道灼.基于模块化多电平的静止无功补偿器故障容错控制[J].电力系统保护与控制,2012,40(16)：83-89.Lian Xiaorang,Jiang Daozhuo.Fault-tolerant design and control of modular multilevel converter-based STATCOM[J].Power System Protection and Control,2012,40(16)：83-89.