基于目标波形与逻辑编-译码的多电平变流器通用调制算法

王立乔 严江涛

（燕山大学电力电子节能与传动控制河北省重点实验室 秦皇岛 066004）

1 引言

多电平变流器由于可直接实现大容量的输出且无需变压器连接，成为当前大容量电力电子设备的重要拓扑结构方案，在大功率传动系统[1,2]、电能质量控制[3,4]及大规模可再生能源利用[5]等场合得到了广泛的应用。

多电平变流器的拓扑结构有二极管钳位型多电平变流器、飞跨电容型多电平变流器及级联型多电平变流器三种基本结构[6,7]。这些基本结构均存在一些问题如元器件数目过于庞大、直流电压难以均衡等。为了解决这些问题，不断有新型的拓扑结构出现，这方面的研究方兴未艾。面对这些新型的拓扑结构，传统的脉宽调制（Pulse Width Modulation，PWM）不再适用，多电平变流器PWM算法的研究也成为热点。

目前，常见的多电平变流器的 PWM 算法有三种：开关角优化 PWM[8,9]、多电平空间矢量调制[10,11]（Space Vector Modulation，SVM）和多载波PWM[12,13]。这些算法都是根据拓扑结构的特点，从二电平PWM算法延伸推广出来的。这些调制算法都有各自的优点，也有各自的不足。开关角优化PWM 是定次谐波消除 PWM 方法在多电平变流器中的拓展应用，具有谐波品质优秀、开关频率低等优点。该算法的一大问题就是开关角的计算问题。传统上开关角的计算需要大量的运算时间，难以实现在线调制。随着微处理器运算速度的大幅度提升和各种新型算法如Walsh变换法[14,15]的引入，开关角的实时计算问题已经得到初步解决。但是对于不同拓扑结构，求解开关角的方程组形式各异，甚至对于同一拓扑结构不同调制比对应的方程组形式也不统一，另外在某些场合中同一方程组的解不具有唯一性[16]，这些问题导致求解开关角的算法过于复杂。还有，开关角优化 PWM计算的基础是按基波周期分解的三角级数，其计算和更新周期就是基波周期。对于那些对实时性和快速性要求较高的应用场合，这样的更新周期过于缓慢。

多电平SVM是两电平SVM在多电平变流器中的扩展应用。多电平 SVM 算法可以方便地使用多电平变流器的开关冗余，因而在解决多电平变流器的中点电位、开关负荷不对称等问题上有显著的优势。多电平 SVM 算法的问题是算法比较复杂，因为多电平变流器的空间矢量数目按电平数的立方级数迅速扩张，其区间判断和占空比运算变得颇为复杂。虽然在这方面出现了很多简化快速算法，但总是需要较为复杂的坐标旋转变换（如六角坐标法[17]）或区间判断方法（如多维坐标系法[18]）。

多载波 PWM是目前多电平变流器实际应用最多的开关调制技术。多载波 PWM具有算法简单、工程实现容易等特点。载波相移 PWM技术已经成为大功率变流设备中常规的开关调制算法。多载波PWM的开放性很强，各种常规的二电平载波PWM算法如SPWM、SVM等都可以扩展为多载波PWM算法。多载波 PWM算法也存在两个方面的问题。一方面是其对多电平变流器的开关冗余利用不足，容易造成中点电位不平衡（对二极管钳位型变流器而言）、开关负荷不对称等问题。另一个方面是对新型拓扑结构的适应问题。多载波 PWM对于三种基本拓扑结构是非常适用的，对于层出不穷的各类新型拓扑结构就难以直接应用，往往需要采用波形的割补和重构等方法[19,20]，失去了算法简单、容易实现的优越性。

上述有关多电平变流器PWM算法的研究仍主要面对三种基本拓扑结构。对于各种新出现的拓扑结构，则需要对几种常规算法进行改造；而为了适应新拓扑的特点，这些改造往往削足适履，丧失原有调制方法的优越性。如果能找到某种不依赖于拓扑结构的、较为简便的通用调制算法，将大大缩短新型拓扑结构的研究和开发周期，为多电平变流器的拓扑结构研究提供强有力的支撑。本文在深入研究多电平变流器基本工作原理的基础上，提出了一种基于目标波形和逻辑编-译码的多电平变流器通用调制算法。该调制算法利用相同电平数不同拓扑结构变流器的等价性，确定新型多电平变流器的目标波形和原始工作波形；再结合新型多电平变流器的开关组合状态，对原始工作波形进行逻辑编译码，最终得到新型多电平变流器的开关工作波形。基于目标波形和逻辑编-译码的多电平变流器通用调制算法，具有原理简单、实现容易和通用性强等优点，适用于各种多电平变流器结构。

2 基于目标波形与逻辑编-译码的通用调制算法基本原理

对于任意一种多电平变流器拓扑结构（不妨称之为实际变流器），当电平数确定以后，总可以找到一种电平数与之相同的基本拓扑结构变流器（不妨称之为等价变流器）与之等价。等价变流器的调制算法都已成型，可以按照某种具体的调制算法（如多载波 PWM法）给出其具体开关器件的工作波形（不妨称之为原始工作波形）和最终的输出波形（即所谓“目标波形”）。由于等价变流器和实际变流器输出电平数相同，因此，实际变流器一定可以获得与目标波形一致的输出波形，而原始工作波形与实际变流器各开关器件的实际工作波形之间必然存在逻辑关系。在求取二者之间逻辑关系时，可以按照以下两个步骤进行：①求取原始工作波形与目标波形之间的逻辑关系（逻辑编码）；②求取目标波形与实际工作波形之间的逻辑关系（逻辑译码），获得原始工作波形与实际工作波形之间的逻辑关系。这就是基于目标波形和逻辑编-译码的多电平变流器通用调制算法，基本原理流程图如图1所示。

图1 基于目标波形和逻辑编-译码的多电平变流器通用调制算法的原理流程图Fig.1 Flow chart of general modulation algorithm of multilevel converters based on target waveform and logic coding/decoding

3 实际变流器和等价变流器的选取

以上已经介绍了基于目标波形与逻辑编-译码的多电平变流器通用调制算法的基本原理，下面通过具体的事例加以说明与验证。

目前，新型多电平变流器的拓扑结构多种多样，本文从中选择混合级联多电平变流器[21,22]作为实际变流器。这主要因为混合级联多电平变流器是一种扩展性极强的多电平变流器构成方法，目前大多数新型多电平变流器的构成思想都与之相关。为了简化起见，本文选择如图2所示的混合级联七电平变流器作为实际变流器拓扑。

图2 混合级联七电平变流器Fig.2 Hybrid cascade seven level converter

图2变流器2H1桥主要用于提升变流器的输出电压，独立直流电源为2E，输出电压为Uout1；2H2桥主要用于改善变流器的输出电压波形，独立直流电源为E，输出电压为Uout2。由变流器的工作原理可知，每个半桥上下两个开关管的驱动波形互补，故实际变流器混合级联七电平变流器独立工作波形有 4个：VT1工作波形 S1、VT4工作波形 S4、VT5工作波形S5和VT8工作波形S8。其中，S1、S4、S5和S8为二值开关函数，当开关管导通时取值为1，反之，取值为0。

常规级联型多电平变流器在三种基本电路拓扑结构中，对于相同的电平数，所需的元器件数最少，实现简单，调制上各种常规算法都能适用。因此本文选择常规级联型多电平变流器为等价变流器。等价变流器级联型七电平主电路结构如图3所示。

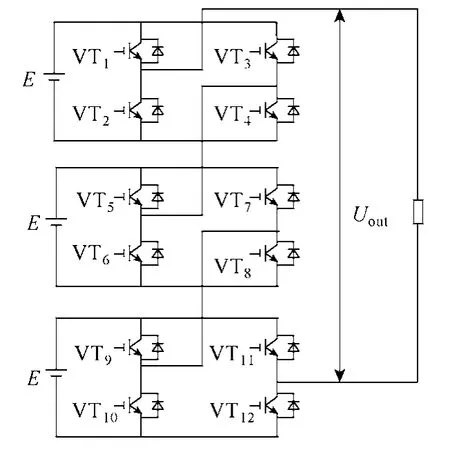
图3 级联型七电平变流器Fig.3 Cascade seven level converter

4 逻辑编码

在实际变流器和等价变流器选定以后，根据图1开始进行逻辑编码。根据级联多电平变流器的工作原理，无论采用何种调制算法，等价变流器中独立的原始工作波形为 6个（即开关管 VT1、VT4、VT5、VT8、VT9和VT12的驱动波形）。逻辑编码就是要求取原始工作波形与目标波形之间的逻辑关系。考虑到等价变流器结构较为复杂，为了把问题说清楚，不妨从最简单的如图4所示的单相桥式逆变器开始说明逻辑编码的过程。

图4 单相桥式逆变器Fig.4 Single phase full-bridge inverter

4.1 单相桥式逆变器的逻辑编码

输出电压Uo与开关管VT1的工作波形g1和VT4的工作波形g4之和存在一一对应的关系，见表1。

表1 输出电压与工作波形之和的关系Tab.1 Relationship between output voltage and operating waveform of Fig.4

经分析可知，二者之间的关系为

从逻辑关系的角度考虑，将g1和g4定义为输入变量，而将输出电压对应的二进制数00～10定义为输出变量，不妨设为A、B。可列出逻辑编码真值见表2。

表2 逻辑编码真值表Tab.2 Real value of logic coding

输入变量g1和g4总共有22=4种组合状态，输出变量个数为2个，这是一个逻辑编码的过程。根据表3，画出其相应的卡诺图，如图5所示。

图5 逻辑编码卡诺图Fig.5 Karnaugh map of logic coding

根据卡诺图 5，可以化简得到工作波形与输出波形的逻辑关系

4.2 等价变流器的逻辑编码

对于图3所示的级联七电平变流器，输出电压波形由开关管 VT1、VT4、VT5、VT8、VT9和 VT12的工作波形（即原始工作波形）共同决定。

引入二值逻辑开关函数

输出电压与原始工作波形之和的关系如表3所示。经分析可知，二者之间的关系为

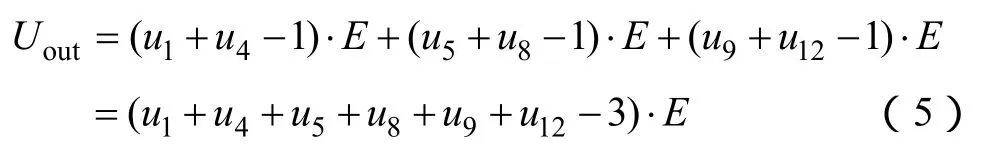
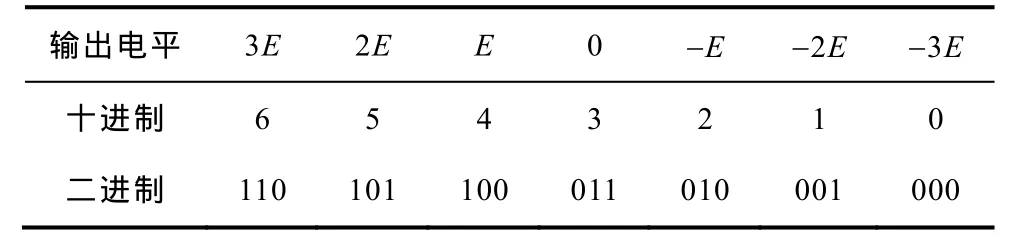
表3 输出电压与工作波形之和的关系Tab.3 Relationship between output voltage and operating waveform of seven level converter

将u1、u4、u5、u8、u9和u12定义为输入变量，总共有26=64种组合状态。而将输出电压对应的三位二进制数000～110，按照位数从高到低，定义为3个输出变量A、B、C。以输出电平为E（即ABC=100）为例，输入变量组合状态见表 4。从表 4中可以看出，仅在输出电平为E时，就存在 15种组合方式，其真值表形式较复杂，卡诺图化简较困难，可借助于计算机高级仿真语言实现这种逻辑编码过程。

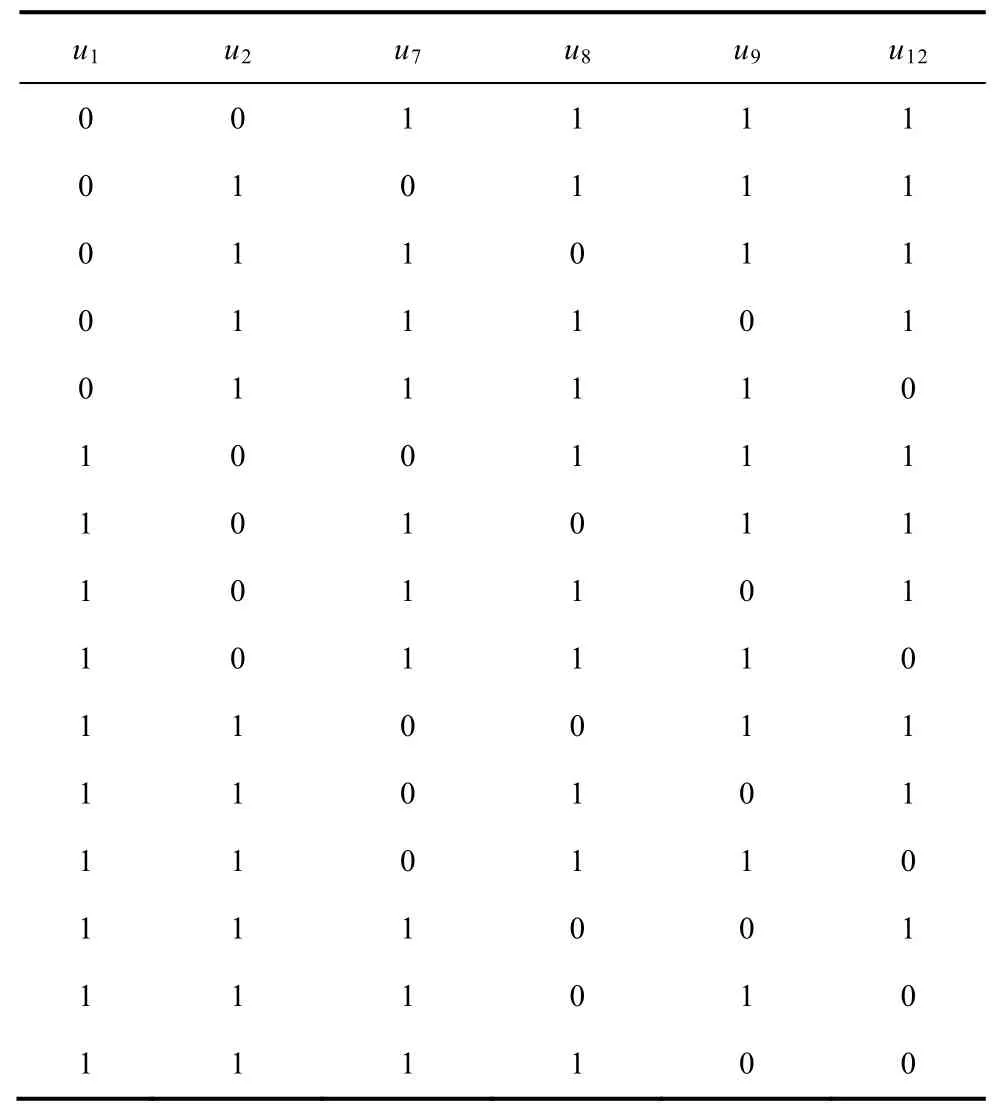
表4 输出电平为E时的开关组合状态Tab.4 Switch combination with output levelE

5 逻辑译码

对于图2所示的实际变流器混合级联七电平电路，容易得到混合级联七电平各个开关状态与输出电平的关系见表 5。从表 5可以看出，混合级联七电平变流器中，在输出电平为±E时，分别存在两种开关状态：第一种开关状态输出电压E是通过2H1桥输出 2E和 2H2桥输出-E获得，-E是通过 2H1桥输出-2E和2H2桥输出E获得，本文称之为有电流倒灌的工作方式；第二种开关状态输出电压E是通过2H1桥输出0和2H2桥输出E获得，-E是通过2H1桥输出0和2H2桥输出-E获得，本文称之为无电流倒灌的工作方式。混合级联多电平的传统调制方式只能实现有电流倒灌的工作方式，而这种工作方式会产生两方面的不利影响：①直流电源必须是可逆直流源，这增加了系统成本；②从能量流动的角度考虑，在电流倒灌时刻，电源在发出功率时还要吸收一部分功率，功率流动过程中会产生不必要的损耗，从而降低了系统的效率。为此，本文只研究无电流倒灌的工作方式。

表5 混合级联7电平变流器开关状态与输出电平的关系Tab.5 Relationship between switch state and output level of hybrid cascade seven level converter

对于混合级联七电平变流器，输出电平为-3E～3E，对应的二进制表达式取为000～110，与表3中等价变流器输出电压的对应二进制表达式一致。从逻辑电路的角度考虑，将输出电平数的二进制表达式作为输入变量，个数为3个，即上小节逻辑编码的结果A、B、C。将S1、S4、S5、S8定义为输出变量，则目标波形与实际工作波形的逻辑关系即是从A、B、C到S1、S4、S5、S8的映射关系，可用译码实现，逻辑译码真值见表6。根据表6，画出相应的卡诺图，如图6所示。

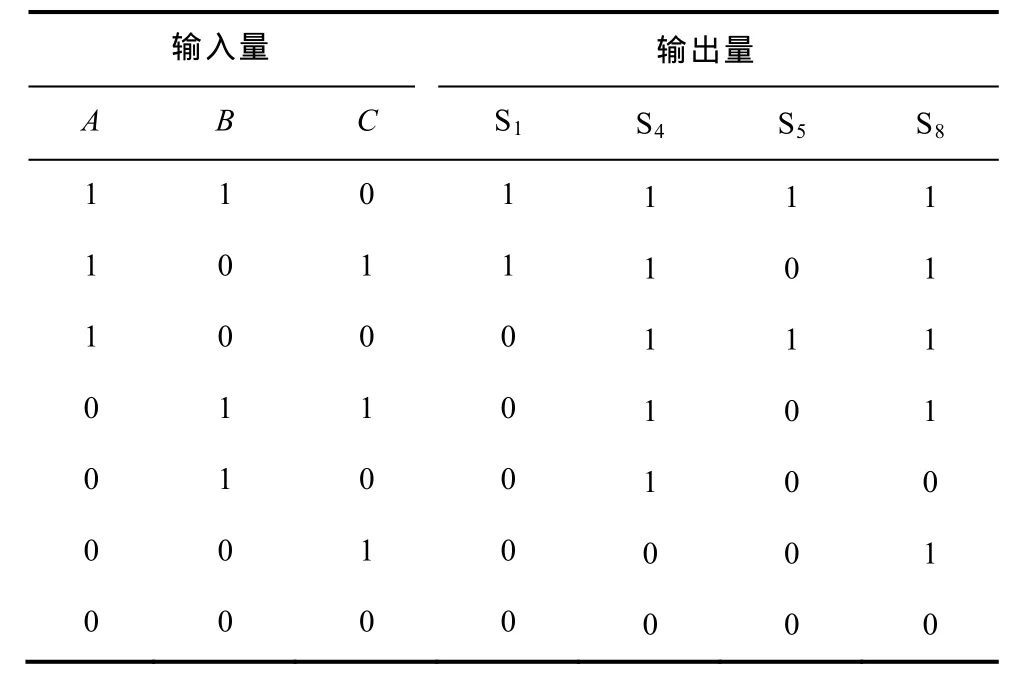
表6 逻辑译码真值表Tab.6 Real value of logic decoding

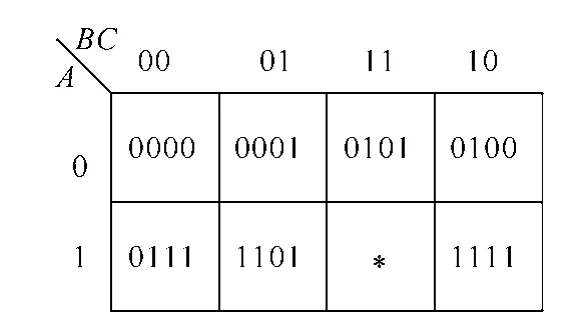
图6 逻辑译码卡诺图Fig.6 Karnaugh map of logic decoding

由图6化简得到混合级联七电平变流器各个开关管的实际工作波形为

6 仿真和试验验证

前面已经给出了基于目标波形和逻辑编-译码的多电平变流器通用调制算法的基本原理，并以混合级联七电平变流器为实际变流器、常规级联七电平变流器为等价变流器，完成了逻辑编码和译码，得到了实际工作波形。下面给出仿真和试验验证。

6.1 仿真验证

从以上的分析可以看出，原始工作波形的获得可以采用任何一种常规调制算法，下面分别以常见的载波相移PWM法为例，对所提出的调制算法进行仿真验证。

6.1.1混合级联七电平变流器的仿真验证

混合级联七电平变流器的仿真工作波形如图 7所示。其仿真参数为：三角载波频率f=200Hz，调制比m=0.8，直流侧输入电压：2H1桥直流侧输入电压U1=100V，2H2桥直流侧输入电压U2=50V，采用电阻性负载RL=10Ω。图7a为载波相移PWM方法的调制波和6列依次相移60°的三角载波，图7b和图7c分别为原始工作波形和目标波形。图7d为经过逻辑编-译码，并按照式（6）～式（9）得到的工作波形。图 7e为混合级联七电平变流器的最终输出波形，与目标波形图7c完全一致。图7f为2H2桥电流波形，可见无电流倒灌现象出现。

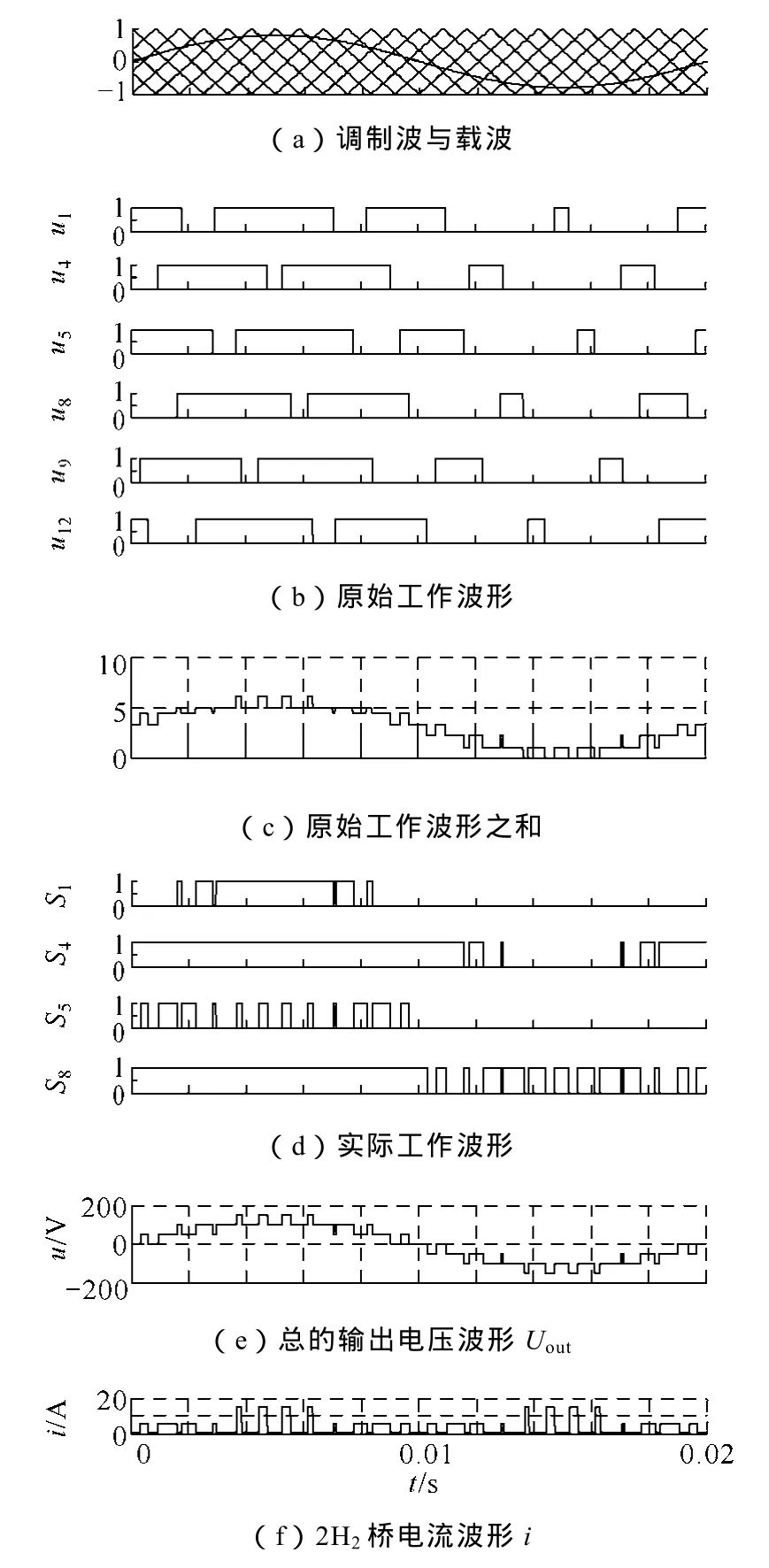
图7 所提通用调制算法在混合级联七电平变流器中应用的仿真波形Fig.7 Simulation waveforms of proposed general modulation algorithm applied to hybrid cascade seven level converter

输出电压波形（见图 7c）的谐波特性如图 8所示，可见谐波分布在1 200Hz附近，即载波频率的6倍频附近，与载波相移SPWM的输出谐波特性完全一致[22,23]。

图8 混合级联七电平变流器输出电压谐波分析Fig.8 Output voltage harmonics analysis of hybrid cascade seven level converter

6.1.2通用性仿真验证

为了对所提调制算法的通用性进行验证，选择另一种新型多电平变流器拓扑结构[24]（见图 9）进行仿真试验。图9所示变流器已经突破桥式变流器的结构（当然，该电路仍然保留了电压型桥式变换器的一个基本特征，即同一半桥上下两个器件的驱动信号互补导通），大大不同于三种基本电路拓扑，已无法应用传统的调制算法对其进行调制。由于该电路可以实现七电平输出，因此，等价变流器同样选择级联七电平变流器。

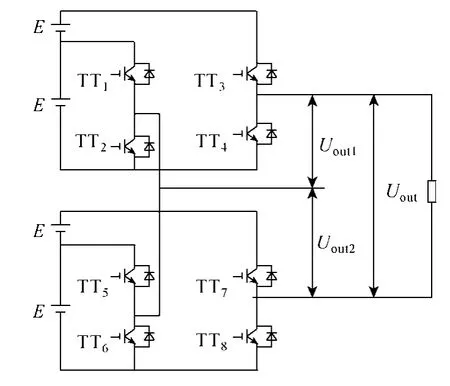
图9 另一种新型七电平变流器拓扑Fig.9 Another new seven level converter topology

由于仍然是七电平变流器，因而编码的过程与结果与前面完全相同，不同之处在于译码。由于图9变流器输出电平的开关组合与图 2完全不同，因而需重新进行译码。从这里可以看出，本文所言的通用性可从两个方面进行更深入的阐释。一方面，是方法或者思维的通用性，即图1流程图所示的调制方法本身对所有多电平变流器都是通用的。另一方面，是具体实施过程中的通用性，即电平数和目标波形相同的不同结构变流器在编码时的过程和结果是完全相同的，具有通用性。而本文所提调制算法的译码部分，则体现了不同拓扑结构变流器的差异性或个性。根据图9变流器自身的开关组合状态，译码得到TT1、TT4、TT5和TT8的实际驱动波形SS1、SS4、SS5和SS8的逻辑表达式为

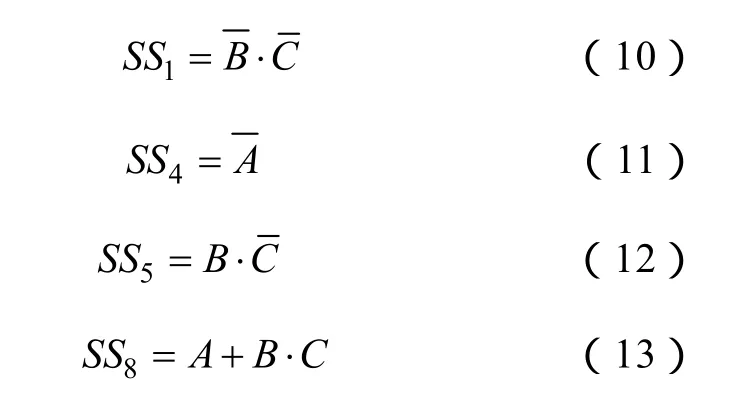
按照以上的结果，进行仿真验证。仿真参数：载波三角波频率f=200Hz；调制比m=0.8；直流侧输入电压：E=50V；采用电阻性负载RL=10Ω。仿真工作波形如图10所示。

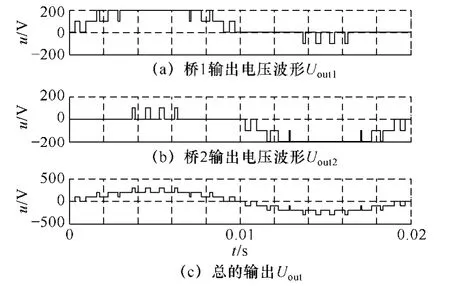
图10 新型七电平变流器工作波形Fig.10 Operating waveforms of new seven level converter

对比图10和图7，可以发现虽然电路拓扑结构完全不同，但在电平数和目标波形相同的情况下，两种七电平变流器的输出波形完全一致，这也验证了本文所提调制算法具有不依赖于拓扑结构的通用性。

6.2 试验验证

在理论分析和仿真研究的基础上，本文构造了混合级联七电平变流器，试验验证了基于目标波形和逻辑编-译码的通用调制算法。主电路如图 2所示，直流侧采用单相不控整流桥供电，2H1桥输入电压为100V，2H2桥输入电压为50V，负载为阻感性负载。目标波形通过载波相移 PWM实现，三角载波频率取1kHz，调制比为0.8。

图 11所示是开关器件 VT1、VT4、VT5和 VT8的触发脉冲波形。图12是两个2H桥功率单元各自的输出电压波形。

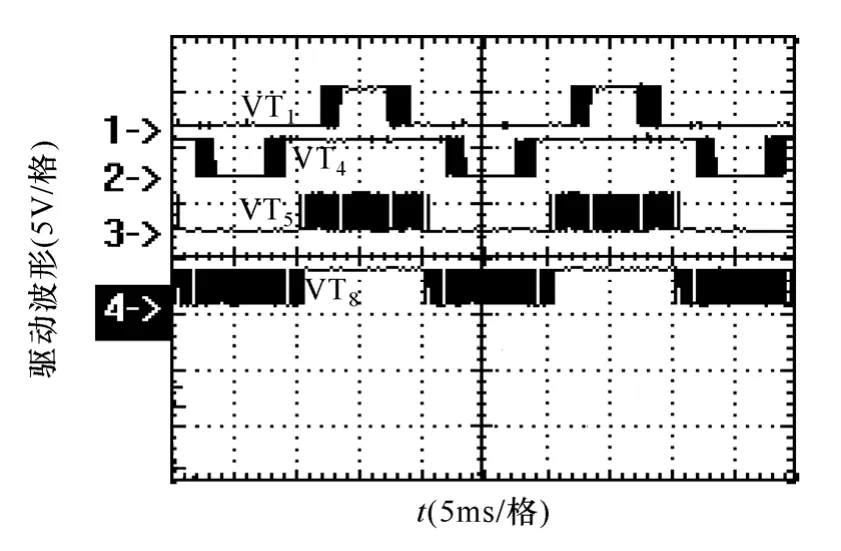
图11 各开关器件驱动波形Fig.11 Trigger waveform of devices

图12 两单元各自输出电压波形Fig.12 Output voltage waveforms of two units

图13 多电平变流器输出电压、电流波形及输出电压频谱Fig.13 Output voltage/current waveform and output voltage spectra of multilevel converter

混合级联七电平变流器的输出电压和负载电流试验波形如图13a所示，输出电压频谱如图13b所示。从图13b可以看出，输出电压的频谱输出电压谐波主要集中在载波频率 6kHz左右，输出电压谐波主要集中在6倍频的三角载波频率处，与目标波形的理论频谱特征完全一致[22,23]。试验结果验证了基于目标波形与逻辑编-译码的多电平变流器通用调制算法的正确性。

7 讨论

本文所提通用调制算法的关键之处就是编码和译码。从上文给出的例证中，可以看出译码部分相对简单，手工化简卡诺图即可完成；编码部分则过于复杂，难以通过手工完成化简，即使借助高级程序语言实现了化简，其所用逻辑门数也非常多。如果采用分离器件，一来过于复杂，同时由于各器件参数的不一致性和分散性，还可能导致最终结果的畸变。因此，本文采用FPGA完成逻辑编-译码。对于本文提到的两种七电平变流器而言，采用 FPGA完成逻辑编-译码所需的逻辑门数基本相同，都在50个左右，因而也可以采用逻辑门数较少的CPLD实现。

本文所举的例子为七电平变流器，当电平数增长时，本文所提调制算法所需的逻辑门数见表 7。可见，当电平数增长时，所需的逻辑门数会逐渐增多；但这种增长是一种有限的增长，当电平数达到一定多的时候，所需的逻辑门数的增长速度反而会变慢。另外，即使是15电平变流器，所需逻辑门数也不过150个，对于常用的数千门数的FPGA而言，占用的资源实际上是非常有限。

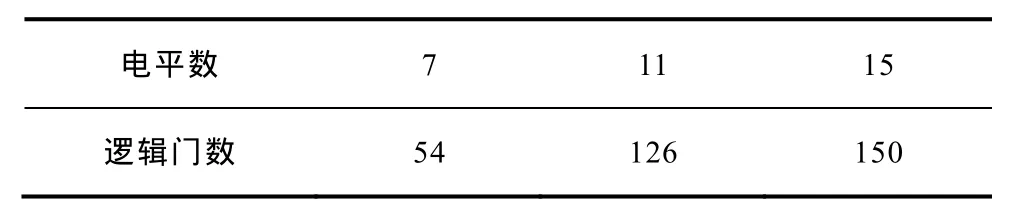
表7 不同电平变流器所提调制算法需要的逻辑门数Tab.7 Numbers of logic gates demanded with proposed modulation algorithm by different levels converters

8 结论

为了适应不断出现的新型多电平变流器拓扑结构，本文提出了基于目标波形与逻辑编-译码的多电平变流器通用调制算法。考虑到电平数相同的不同电路拓扑可以得到相同的输出波形，也就是电平数相同的不同电路拓扑在输出上相互等价。只要找到等价变流器与实际变流器开关工作波形的相互逻辑关系，就可以用等价变流器的调制算法实现实际变流器的调制。这种等价关系可以用逻辑编-译码的方法实现，这就是基于目标波形与逻辑编-译码的多电平变流器通用调制算法的基本原理。以混合级联多电平变流器为例，对该调制算法进行了理论分析、仿真和试验验证。仿真和试验结果表明基于目标波形与逻辑编-译码的多电平变流器通用调制算法，具有不依赖于具体拓扑结构的通用性，算法简单且容易实现，适用于各种结构的多电平变流器，具有良好的应用前景。

[1] Hammond P W. Medium voltage PWM drive and method: U.S., 5 625 545[P]. Apr. 1997.

[2] 刘文华, 陈远华, 张新成, 等. 混合七电平逆变器的变频调速PWM控制策略[J]. 中国电机工程学报,2004, 24(11): 59-63.

Liu Wenhua, Chen Yuanhua, Zhang Xincheng, et al.Variable frequency drive PWM control strategy for hybrid 7-level inverter[J]. Proceedings of the CSEE,2004, 24(11): 59-63.

[3] 李建林, 赵栋利, 赵斌, 等. 载波相移 SPWM 级联H型变流器及其在有源电力滤波器中的应用[J]. 中国电机工程学报, 2006, 26(10): 109-113.

Li Jianlin, Zhao Dongli, Zhao Bin, et al. Cascade H-bridge converter with carrier phase shifted SPWM technique and its application in active power filter [J].Proceedings of the CSEE, 2006, 26(10): 109-113.

[4] 王立乔, 邬伟扬. 错时采样空间矢量调制的级联型多电平变流器及其在并联有源电力滤波器中的应用[J]. 电工技术学报, 2006, 21(12): 90-97.

Wang Liqiao, Wu Weiyang. Cascade multilevel converter based on sample time staggered space vector modulation and its application to shunt active power filter[J]. Transactions of China Electrotechnical Society, 2006, 21(12): 90-97.

[5] 李建林, 朱颖, 胡书举, 等. 风力发电系统中大功率变流器的应用[J]. 高电压技术, 2009, 35(1):169-175.

Li Jianlin, Zhu Ying, Hu Shuju, et al. Topology and modulation strategy for high power converter in wind power system[J]. High Voltage Engineering, 2009,35(1): 169-175.

[6] Peng Fang Zheng, Lai Jihsheng, Mckeever John W. A multilevel-voltage source inverter with separate DC sources for static var generation[J]. IEEE Transactions on Industry Application, 1996, 32(5): 1130-1138.

[7] Lai J S, Peng F Z. Multilevel converters—a new breed of power converters[J]. IEEE Transactions on Industry Application, 1996, 32(3): 509-517.

[8] 卜乐平, 张慧, 刘开培, 等. 非对称优化脉宽组合调制 H-桥级联多电平逆变器的选择性谐波控制[J].电工技术学报, 2011, 26(11): 32-37.

Bu Leping, Zhang Hui. Liu Kaipei, et al. Study of a synthesized unsymmetrical optimal PWM technique of selective harmonic controlling for cascaded h-bridge multi-level inverters[J]. Transactions of China Electrotechnical Society, 2011, 26(11): 32-37.

[9] Tolbert L M, Chiasson J N, Zhong Du, et al. Elimination of harmonics in a multilevel converter with nonequal DC sources[J]. IEEE Transactions on Industry Applications, 2005 , 41(1): 75-82.

[10] Leon J I, Portillo R. New space vector modulation technique for single-phase multilevel converters[J].IEEE Transactions on Industry Applications, 2007,15(7): 617-622.

[11] Sanmin Wei, Bin Wu, Fahai Li, et al. A general space vector PWM control algorithm for multilevel inverters[C]. Proceedings of IEEE Applied Power Electronics Conference and Exposition 2003, Miami Beach, USA,2003, 1: 562-568.

[12] 王立乔, 黄玉水, 刘兆燊, 等. 多电平变流器多载波 PWM 技术的研究[J]. 浙江大学学报(工学版)2005, 39(7): 1025-1030.

Wang Liqiao, Huang Yushui, Liu Zhaoshen, et al.Research on multi-carrier PWM technique for multilevel converters[J]. Journal of Zhejiang University(Engineering Edition), 2005, 39(7): 1025-1030.

[13] McGrath B P, Holmes D G. A comparison of multicarrier PWM strategies for cascaded and neutral point clamped multilevel inverters[C]. Proceedings of IEEE Power Electronics Specialists Conference, Galway,2000, 2: 674-679.

[14] 郑春芳, 张波, 丘东元. 基于沃尔什函数的逆变器选择性谐波消除技术开关角的快速求解[J]. 中国电机工程学报, 2005, 25(22): 39-44.

Zheng Chunfang, Zhang Bo, Qiu Dongyuan. Fastsolving switching angles of inverter’s selected harmonic elimination technique with walsh function[J]. Proceedings of the CSEE, 2005, 25(22): 39-44.

[15] Zheng Chun-fang, Zhang Bo, et al. Selective harmonic elimination technique based on walsh transform for multilevel inverters[J]. Proceedings of the CSEE,2006, 21(7): 121-126.

[16] 张永昌, 赵争鸣. 三电平逆变器 SHEPWM 多组解计算方法[J] 电工技术学报, 2007, 22(1): 74-78.

Zhang Yongchang, Zhao Zhengming. Multiple solutions for selective harmonic eliminated PWM applied to three-level inverter[J]. Transactions of China Electrotechnical Society, 2007, 22(1): 74-78.

[17] Celanovic N, Boroyevich D. A fast space vector modulation algorithm for multilevel three-phase converters[J]. IEEE Transactions on Industry Applications,2001, 37(2): 637-641

[18] Prats M M, Franquelo L G, Portillo R, et al. A 3-D Space vector modulation generalized algorithm for multilevel converters[J]. IEEE Power Electronics Letters, 2003, 1(4): 110-114.

[19] 张杰, 邹云屏, 张贤. 混合级联多电平逆变器研究[J]. 电力电子技术, 2003, 37(4): 16-19.

Zhang Jie, Zou Yunping, Zhang Xian. Research on hybrid cascade multilevel inverter[J]. Power Elctronics,2003, 37(4): 16-19.

[20] 李和明, 王毅, 石新春, 等. 混合级联型多电平变频器拓扑结构研究[J]. 中国电机工程学报, 2006,26(2): 127-132.

Li Heming, Wang Yi, Shi Xinchun, et al. Research on the Hybrid frequency carrier-based multilevel PWM control strategy[J]. Proceedings of the CSEE, 2006,26(2): 127-132.

[21] 孙醒涛, 孙力, 张云. 一种新型电压型逆变器拓扑结构及其 PWM 控制方法[J]. 中国电机工程学报,2008, 23(7): 75-80.

Sun Xingtao, Sun Li, Zhang Yun, et al. Topology and PWM control method of a novel voltage-source inverter[J]. Proceedings of the CSEE, 2008, 23(7):75-80.

[22] 丁凯, 邹云屏, 吴智超, 等. 新型三相混合不对称九电平逆变器研究[J]. 中国电机工程学报, 2005,25(11): 37-40.

Ding Kai, Zou Yunping, Wu Zhichao, et al. Research on a novel three-phase hybrid asymmetric 9-level inverter[J]. Proceedings of the CSEE, 2005, 25(11):37-40.

[23] Zhang Zhongchao, Ooi B T. Forced commutated HVDC and SVC based on phase-shifted multi-converters[J]. IEEE Transactions on Power Delivery,1993, 8(2): 712-718.

[24] 王立乔, 王长永, 黄玉水, 等. 基于相移 SPWM 技术的级联型多电平变流器[J]. 高电压技术, 2002,28(7): 17-18.

Wang Liqiao, Wang Changyong, Huang Yushui, et al.A cascade multi-level converter with phase-shifted SPWM technique[J]. High Voltage Engineering, 2002,28(7): 17-18.

[25] 韩金刚, 汤天浩, 谭新元. 一种新型混合级联型不对称多电平逆变器[J]. 电工技术学报, 2007, 22(12):110-115.

Han Jingang, Tang Tianhao, Tan Xinyuan. A novel hybrid cascade asymmetrical multilevel inverter[J].Transactions of China Electrotechnical Society, 2007,22(12): 110-115.