整体性：探究活动设计的重要原则——从“三角形的外角”的教学优化说起

☉江苏省如皋市石庄镇初级中学　蔡晓严

整体性：探究活动设计的重要原则
——从“三角形的外角”的教学优化说起

☉江苏省如皋市石庄镇初级中学蔡晓严

课堂教学是由多个不同的探究活动串联而成，这些活动一般会附着在学生的认知主线之上，服务于旧知的提取应用和新知的探究生成.所以，很多老师会从教学主线出发来设计课堂活动，以期形成对教师教和学生学有利的“活动串”.然而，在有些课堂上，一个接一个的探究活动缺乏连续性，常会打断学生的思维，将学生的知识获得过程分成若干段，对学生体验数学的整体性十分不利.以人教版八年级上学期“三角形的外角”一课为例，一位老师用5个问题呈现了5个分散的探究活动，学生虽然顺利地获得了新知，但新知的获得是“间歇性”的，他们无法感知到数学知识间的联系，个体数学素养的提升幅度大打折扣.为此，笔者将这些活动进行了适当调整，整合出一个完整的探究活动，通过自主探究，学生不仅获得了新知，还将其与已有“四基”紧密联系在一起.现就呈现这两则教学片断并谈一些思考，希望能给您的教学带来一些启示.

一、一则片断及其优化的分析

教学背景：本节课是人教版八年级上学期的“三角形”第2节的内容，将要学习的“三角形的外角”是“与三角形有关的角”第2课时的内容.上一节课，已经学习了“三角形的内角”，学生具备了应用三角形的内角和定理求内角，以及与内角有关联的角的度数的能力.本节课上，教师已经结合图形，让学生认识了“三角形的外角”.下面的片断中，将重点探究“由三角形内角和定理推出的推论”，也就是三角形外角的性质.

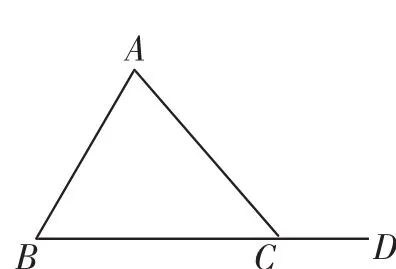
图1

1.原教学片断

问题1：如图1，在△ABC中，∠A＝70°，∠B＝60°，∠ACD是△ABC的一个外角.能由∠A、∠B求出∠ACD吗？如果能，∠ACD与∠A、∠B有什么关系？

学生根据题目中所给出的数据，计算出∠ACD＝ 130°，∠A＋∠B＝130°，根据“数据相等”可以得出“∠ACD＝∠A＋∠B”的结论.

问题2：如果∠A＝30°，∠B＝60°，∠ACD与∠A、∠B还有这样的关系吗？

学生沿用刚才的方法，很快算出∠ACD＝90°，结合“∠A＝30°，∠B＝60°”，归纳得出∠ACD＝∠A＋∠B.

问题3：如果∠A＝130°，∠B＝30°，∠ACD与∠A、∠B还有这样的关系吗？

由于有了前面的经验，学生迅速得出“∠ACD＝∠A＋∠B”这一结论.

教师追问：为什么？

学生还是先求出了∠ACD和∠A＋∠B的度数，然后从“数据相等”的角度对这一关系进行了证明.

问题4：如图1，∠ACD是△ABC的一个外角，∠ACD与∠A、∠B有什么关系？

在稍作停顿后，教师引导学生从∠ACD与∠ACB的位置关系上发现了“∠ACD＋∠ACB＝180°”，然后根据内角和得出“∠A＋∠B＋∠ACB＝180°”，进而证得“∠ACD＝∠A＋∠B”的结论.

问题5：任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系？

学生给出猜想，并结合图1再度进行了说理.接下来，教师将“由三角形内角和定理推出的推论”（即“三角形的一个外角等于与它不相邻的两个内角的和”）进行了板书.

简析：5个问题串起了5个探究活动，学生在这些小的活动的引领下，围绕三角形的外角展开了深入探究.显然，每一个问题都是经过教师精心设计的，活动的要求清晰明了.前三个问题是并列关系，通过探究三种不同三角形（锐角三角形、直角三角形和钝角三角形）中的外角和内角的关系，为后两问的提升归纳做足了铺垫.后两个问题将前三个问题引向深入.在这5个探究活动的链接上，教师起到的作用是巨大的.没有了教师的“穿针引线”，后一个活动是无法得到有效延续的.然而，正是教师的这种频繁“干预”，“一问，一解，一答”，学生在似懂非懂时，教师的介入让他们前一轮的自主探究戛然而止.看似巧妙的过渡语与衔接语，却成为了学生自主思维的“拦路虎”，想要在此时发展思维的深度和广度变成了一件难事.细细分析这5个问题，如果没有了老师的引导，估计学生同样能够给出答案.所以，我们可以将这里的多个活动串联起来一并呈现，让学生的新知探究在一个完整的知识体系中自动进行.

2.优化教学片断

学生活动：先独立思考下面的问题，写下你的结论，然后在小组中交流.

思考：如图1，∠ACD是△ABC的一个外角.

（1）说说图中角的关系；

（2）如果∠A=70°，∠B=60°，求∠ACD的度数，并说说∠ACD与∠A、∠B的关系；

（3）改变∠A、∠B的度数，∠ACD与∠A、∠B还有（1）中你发现的关系吗？如果有，请说明理由，并试着用语言归纳一下你发现的结论.

学生经历了8分钟的独立思考后，在小组中展开交流.15分钟后，小组交流结束.接下来，进行了全班交流，各组同学先后将自己得出的结论或者组内交流得出的结论进行了展示.第（1）题，他们不仅给出了“∠A+∠B+∠ACB=180°”，“∠ACD和∠ACB是邻补角”、“∠ACD+∠ACB=180°”等结论，还给出了“∠ACD=∠A+∠B”、“∠ACD＞∠A”、“∠ACD＞∠B”等结论.教师在肯定同学所给的结论的同时，还通过对结论“∠ACD=∠A+∠B”的即时追问，让学生的交流自然延伸到问题（2）.在交流问题（2）时，教师不仅让学生给出猜想，还让学生在黑板上给出了说理的过程.接下来的追问“这个结论具有一般性吗”，直接过渡到问题（3），多名学生用自己所选择的角度进行了说理，除了较为常见的整数度外，还有学生选择了“∠A=25.5°，∠B=31.2°”和“∠A=65°15′，∠B= 41°2′”进行了验证.最后，在学生将一般情况下的证明过程交流后，教师将结论板书.

简析：本节课的认知基础是三角形的内角，有了上节课的铺垫，加之前面学习的“邻补角”，学生能从图1中获得众多的关系式是正常的，而且他们所得出的这些结论都是较为肤浅的.以“∠ACD=∠A+∠B”为例，只有极少数学生能说清其中的“道道”，所以，教者预设了问题（2）.当他们从问题（1）中获得了众多的结论后，对图1中角之间的关系（位置和数量）有了一个初步的认识，这对问题（2）、（3）的探究是非常有利的.问题（1）给出了猜想，问题（2）给出了方法，问题（3）则给出了证明.在这个探究过程中，学生一旦获得问题（2）的解法，问题（3）的解答就会十分快捷.所以，出现了很多同学别出心裁地选择了一些“古怪”的数据说理是不足为奇的.显然，优化后的探究活动是一个整体，三个问题具有明显的递进关系，突出了数学认知“由特殊到一般”的规律.在这种递进追问中，随着问题的解决，学生的思维呈螺旋式上升，深度和广度得到大幅拓展.接下来的小组和全班的交流，给了每一名学生发表自己见解的机会，不同结论、观点和方法在交流过程中产生碰撞，新知随之生成，个体的数学素养也随之提升.

二、几点启示

1.活动凑零为整，发挥探究的集群效应

整体性，是数学探究活动设计的一个重要原则.在学生的认知活动中，分散的探究，容易分散学生的注意力，不仅不利于学生获得数学“四基”，还不利于学生养成良好是思维品质.因此，我们设计探究活动时，应尽可能将有关联的活动用问题组的形式串在起来，通过问题引领让学生自主探究.这种有意识的“捆绑”，会让多个探究活动发挥出集群效应，形成教学合力，达到“1+1＞2”的教学效果.以本文中的案例为例，笔者对原本单列的5个探究活动进行了调整.充分利用教材，把教材中的“思考”（即问题1）保留下来；为了将定义获得的过程与性质探究的过程准确对接，在原问题1前增加了“说说图中角的关系”的探究；“改变∠A、∠B的度数”，让“∠ACD与∠A、∠B”的关系探究继续，“说明理由”，“并试着用语言归纳结论”，探究由感性上升到理性.三个要求明确的问题一次性呈现，学生在问题的引领下化压力为动力，8分钟的时间，每一名学生都在努力思考，在自己的思维空间中找寻着问题的答案.密集的、不受干扰的思维活动，让学生的生成朝着教师期待的方向前进着，零散的活动在聚集后发挥出了巨大的教学效应.

2.探究一气呵成，强化过程的整体感知

课堂上，零散的探究活动在教师的“穿针引线”下方能发挥其教学价值.为了“穿针引线”，教师会为上下两个单一活动设计能让彼此关联的过渡语.这些过渡语重在承上启下，与知识、技能关联不大.显然，那些对教学成果影响不大的过渡语，过多地呈现反而会打乱学生的思维，分散他们的注意力.所以，为了提升教学语言的“含金量”，我们可以将这些可有可无的过渡弃之不用，将活动直接整合在一起.没有了频繁干扰，学生的主体地位凸显出来，每一个人都是探究活动的主体，他们没有依靠与依赖，问题解决不得不一气呵成，活动过程的体验充分而自然.在上面的“优化设计”中，“思考”是一个整体，个体的探究热情随着问题的抛出迅速被激活，没有了认知替代，每一个人都必须认真梳理自己的知识网络，从中调动出对问题解决可能产生作用的基础知识，比如三角形的内角和定理、邻补角的定义等；为找到问题解决的通道，他们还要努力提取出解读图形和几何说理的经验，在已知与未知之间搭建桥梁；问题解决离不开数学思想的参与，转化、类比等数学思想自主探究中“或隐或现”，促进了个体对这些思想应用价值的体验.应该说，没有了教师的干预，学生的思维得以充分舒展，探究历程个性色彩浓郁，一气呵成.在这一过程中，经验的积累、知识的获得和思想的感悟都是到位的，基于整体的活动设计起到了应有的成效.

3.问题开放设置，培养学生的创新思维

在探究活动中，问题的设计是很有讲究的.不同的教学需求，对问题的要求也不同.当需要唯一答案时，我们就应设计指向明确的问题，让学生沿着唯一的路径给出教者期待的答案；当需要的结果有多种可能时，问题的指向就应含糊一些，只要在题干之下的合理生成都应得到表扬.事实上，很多时候，我们没有必要让学生“一条道走到黑”，问题设计要灵活一些，用开放的问题引领学生对现有基础充分梳理，也许会出现意想不到的收获呢！“说说图中角的关系”，优化后的问题指向“含糊不清”，学生“开足了马力”尽情思考，生成了包括预期的“∠ACD＝∠A＋∠B”在内的6种结果.接下来，“改变∠A、∠B的度数”，让原先“教师给数据探究”转化为了“学生给数据自己探究”，探究更为灵活，结果更为可信.在学生经历的很多探究中，学生都是被动地应用着老师给出的数据，对所获得的结果产生怀疑是难免的，比如本文中优化前的探究就是如此.“自己给数据探究”的闸门打开后，一些“古怪”的数据随之产生，这种情形下的探究结果更容易为学生所接受.问题是开放的，但结果是“收敛”的，教者用开放的问题激活了学生的创新欲望.开放的问题如同一张“大网”，多样的生成如同“网中之鱼”，教师问题设置的指向还是课时“四基”，学生应得的“四基”必在这张“大网”之中.显见，开放设问是一种外在形式上的开放，我们的坚守会让学生不仅获得既定的知识与技能，还会发展学生的创新思维，为学生的可持续发展奠定基础.

三、写在最后

探究活动是数学课堂的重要组成部分，它是课时“四基”的载体，是学生获取这些“四基”的最主要的抓手.为此，我们应该为学生设计与教学内容匹配的探究活动，确保呈现在教学过程中的探究合理而有效.单一活动的容量小，易于操作，用到的知识和获得的知识都比较少；组合探究的活动多，操作有难度，涉及的旧知与生成的知识都比较多.所以，我们在教学设计时，要根据学情、教学内容和教学目标合理选择探究活动的呈现方式，让知识与技能有效融入到探究之中去，当然让学生感受到数学的整体性则是所有活动都必须关注的，无论是单一活动还是组合探究，都应是一个学生能够自主经历的、完整的历程.当我们能够从整体的角度审视自己设计的活动时，我们就已经将学生置于学习的主体地位之上了.此时，我们不再只关注于知识和技能，更多地将会关注“学生能否不受干扰地学习，能否快乐地自主学习”，他们成为了课堂的主人，这不正是我们所期待的生本课堂吗？

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.印冬建.突出核心主线追求有效教学——谈初中数学有效备课的做法和思考［J］.中学数学（下），2014（1）.