基于HMM校正与神经网络延拓的EMD端点效应抑制方法

孟　宗　闫晓丽　王　赛

1.河北省测试计量技术及仪器重点实验室(燕山大学)，秦皇岛，0660042.国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，0660043.长城汽车股份有限公司技术中心(河北省汽车工程技术研究中心)，保定，071000



基于HMM校正与神经网络延拓的EMD端点效应抑制方法

孟宗1,2闫晓丽1王赛3

1.河北省测试计量技术及仪器重点实验室(燕山大学)，秦皇岛，0660042.国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，0660043.长城汽车股份有限公司技术中心(河北省汽车工程技术研究中心)，保定，071000

针对神经网络延拓方法在抑制经验模态分解的端点效应时存在的延拓数据与真实数据往往存在误差的问题，提出了一种基于HMM校正的方法来减小预测延拓数据误差。首先利用径向基函数(RBF)神经网络预测估计方法对部分原始数据进行估计，同时对端点外数据进行预测。然后计算该方法估计的数据与真实数据的误差序列,再用HMM方法建立估计误差序列模型，用以预测延拓后数据的误差。最后用RBF神经网络延拓数据减去HMM预测的误差数据得到新的校正后延拓数据。仿真与实验证明了将HMM预测方法与RBF神经网络数据延拓结合应用到解决端点效应的过程中所得到的延拓数据更接近真实数据，能够更好地解决端点效应问题，提高了经验模态分解精度。

隐马尔科夫模型；误差校正；神经网络；端点效应；经验模态分解

0　引言

自1998年经验模态分解(empirical mode decomposition, EMD)由Huang等[1]提出后,因其优异的时频分析能力被广泛应用到各种信号处理领域[2-5]。EMD时频分析方法的特色是使非平稳信号通过EMD分解平稳化，将不同尺度波动或趋势逐级分解，获得本征模态函数(intrinsic mode function, IMF)。该方法适合非线性、非平稳信号的分析，也适合于线性、平稳的信号分析。然而经过多年的发展，EMD方法仍然存在一些问题需要继续完善。其中端点效应(也称为边缘效应)的存在严重影响了EMD方法的分解效果[6]。端点效应是指用样条函数拟合信号的上下包络线时，因不能确定信号的两个端点是否为极值点，同时端点附近没有端点以外信号的约束，使得拟合得到的包络线在端点附近偏离原信号实际包络线的现象[7]。端点效应使分解过程中数据两端产生发散的结果使得整个序列被“污染”而严重失真。国内外学者针对端点效应先后提出了一些抑制方法[8-11]，其中相当一部分是利用数据预测延拓技术来抑制端点效应。这些方法对抑制端点效应都有一定的效果，但仍然存在着各自的局限性，其主要原因是非线性、非平稳信号是一个不确定的信号，无规律可循，所以无法准确预测它将要出现的信号值，只能借助一些现有算法对其进行估计，因而会存在估计误差。预测误差服从特定的概率分布。若能从各预测算法的预测数据中找到预测误差的变化规律，就可以对预测误差和预测数据进行修正。

本文尝试通过寻找误差序列内在的驱动机制规律来研究误差序列，发现估计误差序列服从隐马尔科夫模型(hidden Markov model,HMM)分布，进而建立HMM[12]，预测延拓数据与真实数据之间可能的估计误差，并利用预测的估计误差对延拓数据进行校正，从而使延拓数据更接近真实值，更加有效地抑制EMD方法的端点效应。

本文利用神经网络对数据进行预测估计，然后基于HMM的误差预测算法对神经网络预测数据进行校正，以达到抑制端点效应的目的。

1　经验模态分解方法及其端点效应

1.1经验模态分解方法

经验模态分解就是对信号进行平稳化处理，即将信号中不同尺度波动或趋势逐级分解开，产生具有不同特征尺度的一系列数据序列，使每个序列组成一个IMF分量。IMF必须满足两个条件：一是每一序列的极值点和过零点数目必须相等或相差不多；二是对于序列中的任意点，由局部极大值构成的包络线和局部极小值构成的包络线的平均值为零。为了把各IMF分量从数据中提取出来，EMD方法通过逐步的“筛选”将多分量信号分解成多个单分量信号。该方法的分解过程如下。

(1)找出原信号x(t)所有局部极值点，用三次样条插值函数分别拟合局部极大值和局部极小值，形成数据上下包络线。x(t)减去上包络和下包络的均值m1得到h1:

x(t)-m1=h1

(1)

在理想情况下，h1应为第一个IMF，但实际上，包络的拟合过冲和欠冲是很普遍的，这样会产生新的极值点，移位或放大已存在的极值点。“筛”的过程必须多次进行。第二次把第一次的h1看作原数据，求出h1的包络平均m11，“筛”的过程表示为

h1-m11=h11

(2)

该过程重复进行k次，直到第k次满足滤波条件得到第一个IMF分量c1。c1表示信号在局部时刻频率最高的成分。

(2)由“筛”的过程可看出，本征模态函数c1包含了原始数据最小尺度或短周期成分，用x(t)减去第一个本征模态函数c1得到残余r1：

x(t)-c1=r1

(3)

若r1中还包含一些长周期成分，就对r1重复步骤(1)得到第二个本征模态分量c2。这样不断重复便可得

(4)

若残余ri分解成一个单调函数则停止，若数据有趋势则残余rn即为趋势项，由式(3)和式(4)可得

(5)

这样就把一个数据分解成本征模态函数组与残余量之和。

1.2端点效应

在经验模态分解中，求包络平均是通过对原始数据中的上极值点和下极值点分别进行样条插值拟合再平均。样条插值的过程中，由于不能确定断点处就是极值点，会在样条插值的过程中产生数据的拟合误差。在经验模态分解“筛”的过程中，由于端点处极值的不确定性，在端点附近没有端点外信息的约束，每一次样条插值都产生较大的拟合误差。在“筛分”过程中，误差不断累计，就会由端点处向内扩散，最后在严重的条件下使数据的分解失去实际意义。

本文首先通过对数值仿真信号进行经验模态分解，对出现的端点效应进行分析，仿真信号为

x(t)=2cos8πt+0.5cos4πt+0.5cosπt

(6)

t∈[-0.45,0.45]

信号为三个余弦信号的叠加，未经数据延拓的原信号与信号的上下包络线如图1所示，其中虚线为信号上包络线，点划线为信号的下包络线，数据序列比较短，不能包含所有数据，因此包络线出现了严重失真，产生了图2所示的端点效应。图2中，点划线表示信号经EMD分解后的IMF分量，实线代表真实的信号分量，经对比发现经验模态分解对信号的处理过程会因为端点效应“污染”而出现较大偏差。其中，c3与真实信号的偏差已经很大，EMD分解结果严重失真，不能准确反映真实信号的成分。所以在EMD处理前，端点效应成为必须解决的问题，否则EMD分解将失去意义。

图1　原始信号及其上下包络线

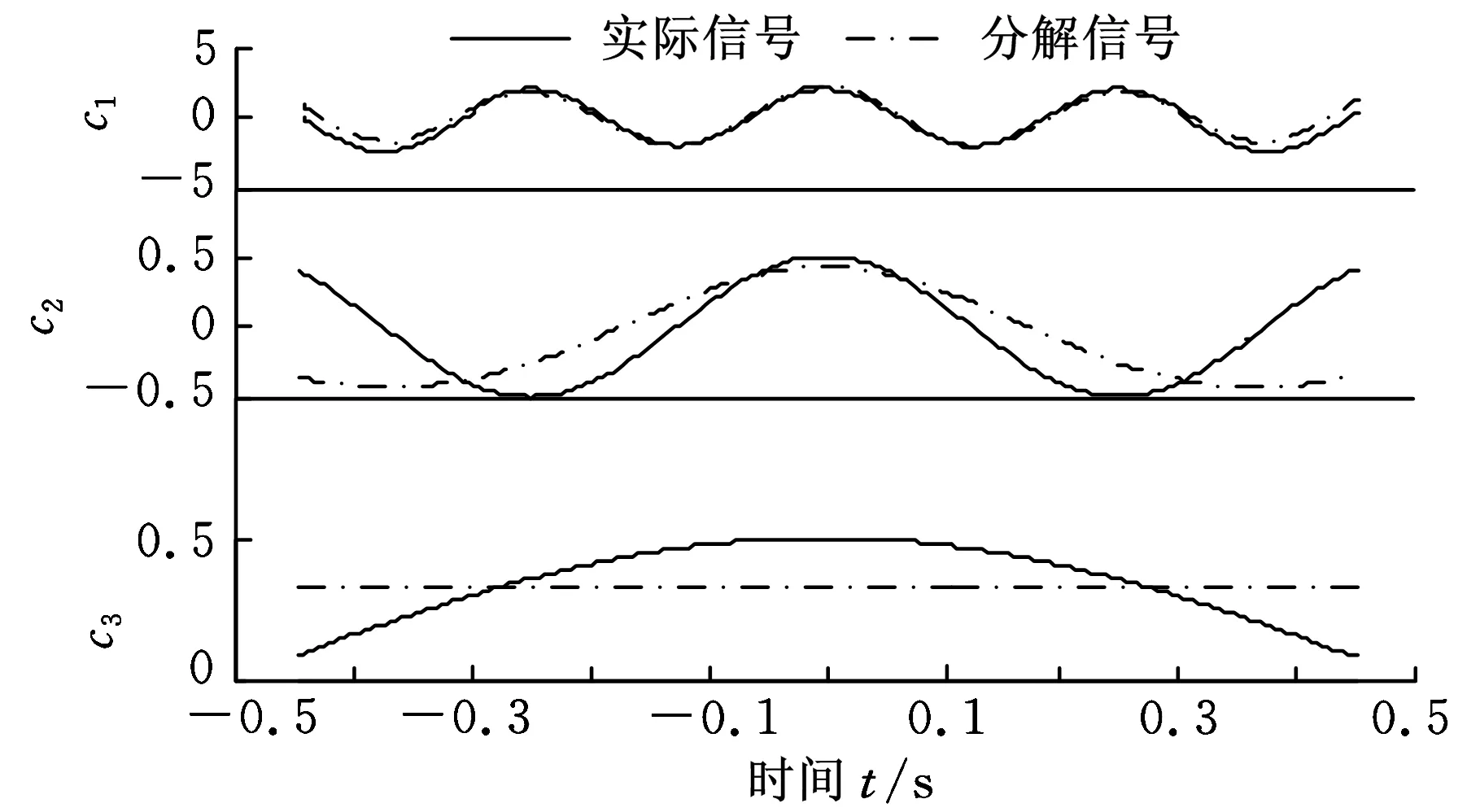
图2　端点效应处理前的EMD分解结果

2　基于神经网络的数据预测延拓法

基于神经网络的数据预测延拓法通过两步实现。第一步是学习过程。对时间序列延拓是根据信号的具体表现形式和端点处的具体特性来进行的。在数据两端利用神经网络延拓出极值点。按照一定规则产生给定数据序列的学习样本矩阵Pm×k，矩阵学习的目的是确定权重向量Wi和偏移向量bi的值，这些量之间的关系为

(7)

其中，f为传递函数，ni为传递函数的输入构成的中间函数。得到的模拟向量al×k与目标向量tl×k会存在偏差。一般用最小二乘法调整权重向量W和偏移向量b的值，使偏差达到最小。由最速下降法得到W和b的值，学习过程结束。第二步为延拓过程。根据学习过程得到的W和b值通过给定的边界处样本矩阵，利用式(7)计算延拓值。采用RBF神经网络对端点外数据进行延拓，把相邻50个连续数据样本进行训练，将得到的训练样本输入网络中训练网络，用训练过的网络对原始信号进行预测，图3所示为对神经网络延拓后的信号进行经验模态分解得到的IMF分量，可看出延拓后信号较接近真实信号。但与真实的IMF分量相比还有一定差距，尤其是IMF与真实数据间误差较大，EMD分解不能完全反映真实数据。

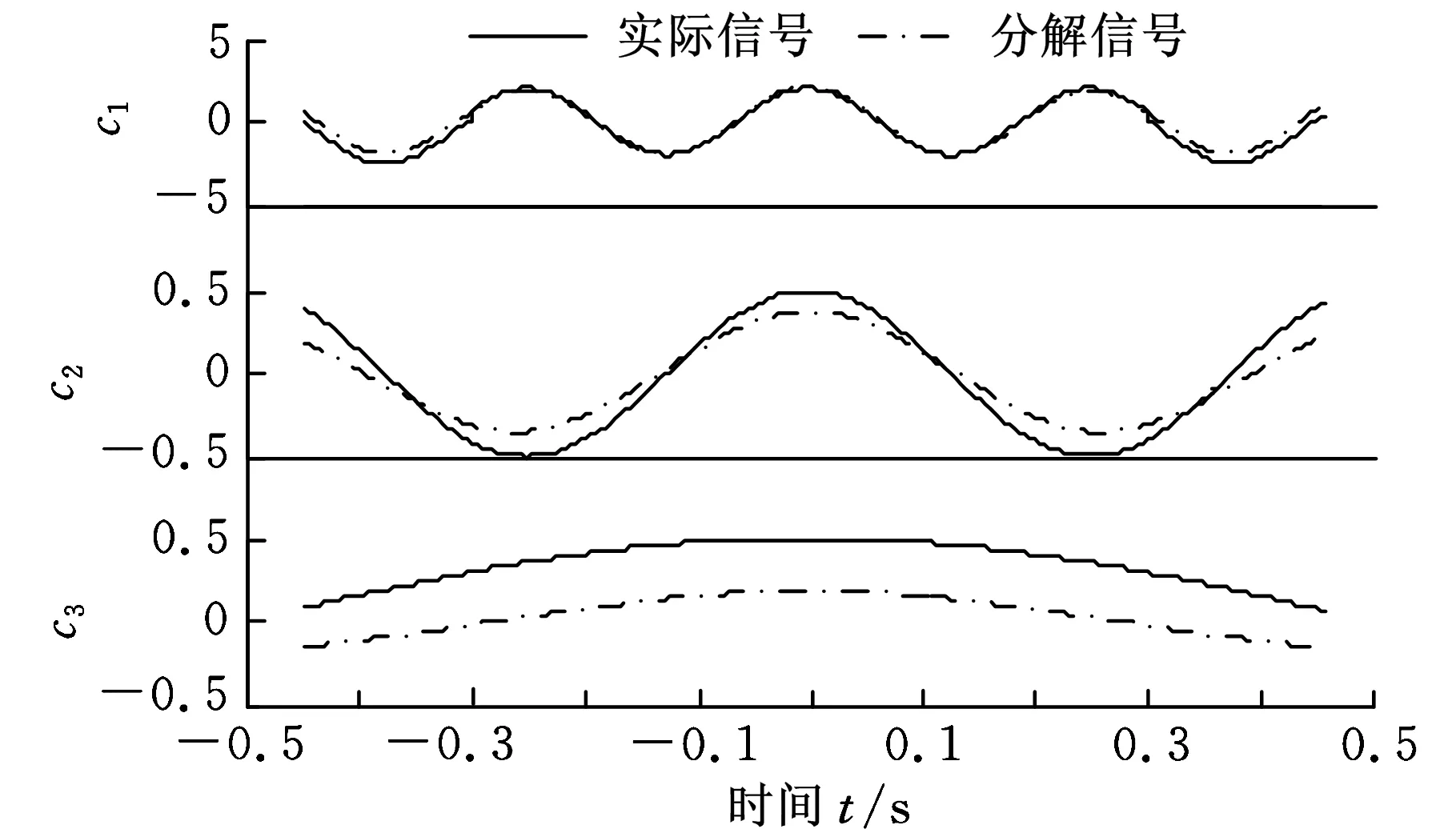
图3　经RBF神经网络延拓后的EMD分解结果

3　基于HMM的预测数据校正算法

3.1基于HMM的预测算法

HMM是重要的统计模型之一，能够有效解决系统中表层事件可能由底层事件引发而产生的一类问题。一般来说，HMM模型的基本要素包括以下内容。

(1)系统初始状态概率分布π。π可表示为

πi=P(qt=Si)i=1,2,…,N

(8)

其中，Si属于隐状态集合S={S1,S2,…,SN}；N为状态数；用qt=Si表示HMM在时刻t处于隐状态Si；隐状态序列Q={q1,q2,…,qN}。

(2)状态转移概率分布矩阵A。A可表示为

A={aij}

(9)

aij=P{qt+1=Sj|qt=Si}i,j=1,2,…,N

(3)观测变量概率分布矩阵B。B可表示为

B={bi(ν)，i=1,2,…,N，ν∈V}

(10)

bi(ν)=P{Qt=ν|qt=Si}

其中，V为观测变量的样本空间；Ot为t时刻观测随机变量。观测序列记为O={O1,O2,…,Ot}。

可以用λ={A,B,π}完整地描述一个HMM(HMM按输出类型分为离散型和连续型)。建立一个标准的HMM需要解决模型参训练、估计隐状态和似然概率计算三个基本问题。

将经各种数据预测的延拓数据与真实数据的误差看作预测误差et。任何时间序列的噪声都服从特定的概率分布，假设观测噪声服从HMM过程，预测算法的实质为通过HMM相关理论对观测序列E={e1,e2,…,et}进行研究和参数估计，然后进行预测。

将数据延拓方法的预测偏高、偏低或正常3种情况看作HMM的3个隐状态。根据预测误差分布情况，将预测误差分成N类，作为HMM的一系列观测值，并分析隐状态与观测值之间的对应关系。由此建立预测误差HMM，确定模型参数，利用模型的状态转移概率矩阵和观测值概率矩阵对预测误差进行预测。最后利用预测误差对延拓数据进行校正。

对预测误差建立HMM，首先要进行HMM训练，具体步骤如下。

(1)利用聚类算法将观测数据分为5类，大致为偏高值较大、偏高值较小、较接近真实数据、偏低值较大、偏低值较小与偏低值较大5类数据，将误差序列聚类为5种观测值后，通过阈值形成新的观察值序列。即

(11)

其中，Ire为预测误差与真实数据的百分比。阈值分别取20%、40%、60%、80%，在分析数据时用测试误差的离散化阈值H=[P0.2P0.4P0.5P0.6P0.8]T进行还原。

(2)得到观测值序列后，对观测值进行训练建立HMM，得到HMM的状态转移概率矩阵A与观测值概率矩阵B。

(12)

3.2基于HMM预测和神经网络的数据延拓方法

经神经网络延拓数据后，在计算与真实数据的延拓误差的基础上得到误差序列。然后对误差序列建立HMM，并预测延拓误差，校正神经网络延拓数据，具体流程如图4所示。

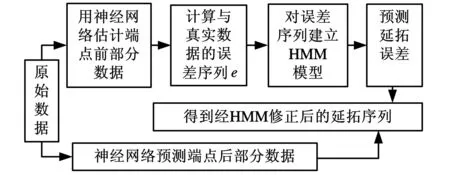
图4　基于HMM和神经网络的数据延拓流程

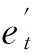
(13)

对神经网络的预测序列进行校正得到的信号再进行EMD分解，抛弃端点外数据得到图5所示的分解结果。

图5　校正后的EMD分解结果

分解精度为

(14)

其中，M表示信号的分量数目，N表示信号采样点的个数，xi(k)与ci(k)分别表示原信号与分解后的第i个分量。由式(14)可知，E越小，说明EMD的分解效果越好，相应端点效应的抑制效果也就越好。

将文中的仿真信号经过不同的端点效应处理方法进行处理后进行EMD分解，计算不同的端点效应处理方法得到的EMD分解精度，见表1。

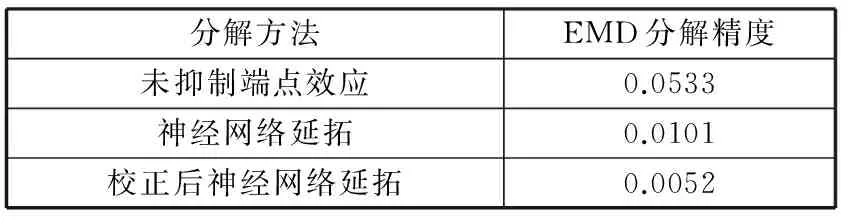
表1　各方法精度比较

由表1可以看出，经HMM算法校正后神经网络延拓数据的EMD分解精度明显高于未进行端点效应抑制的分解精度，也高于未进行HMM校正而直接进行神经网络延拓的分解精度。

4　实验研究

通过对转子实验台的支撑部件连接松动实验数据进行分析来验证基于HMM校正与神经网络延拓的EMD端点效应抑制方法的有效性。在实验台上将固定轴承的螺丝拧松，模拟转子系统的支撑松动故障，测转子圆盘的径向位移的振动信号，转速为924 r/min，采样频率为3 kHz。圆盘的径向位移信号如图6所示。

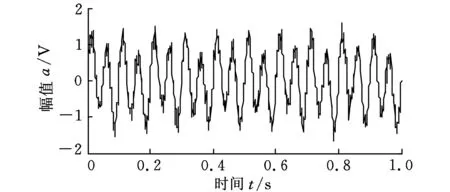
图6　转子支撑松动故障信号

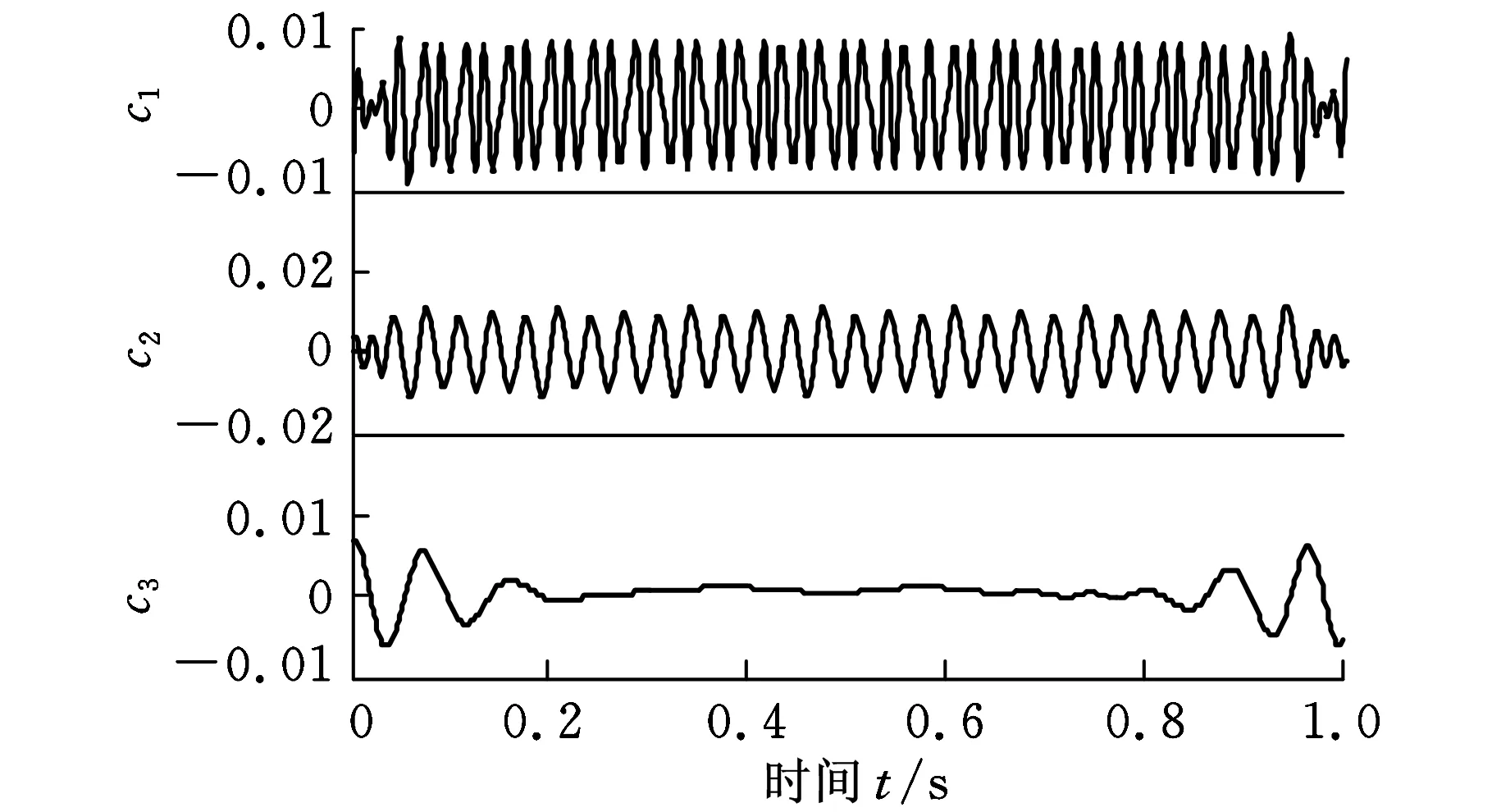
对实验数据直接进行EMD分解，得到图7所示的分解效果与时频谱图。先对信号利用RBF神经网络延拓抑制端点效应后再进行EMD分解,得到图8所示的EMD分解结果与时频谱图。

(a)EMD分解结果

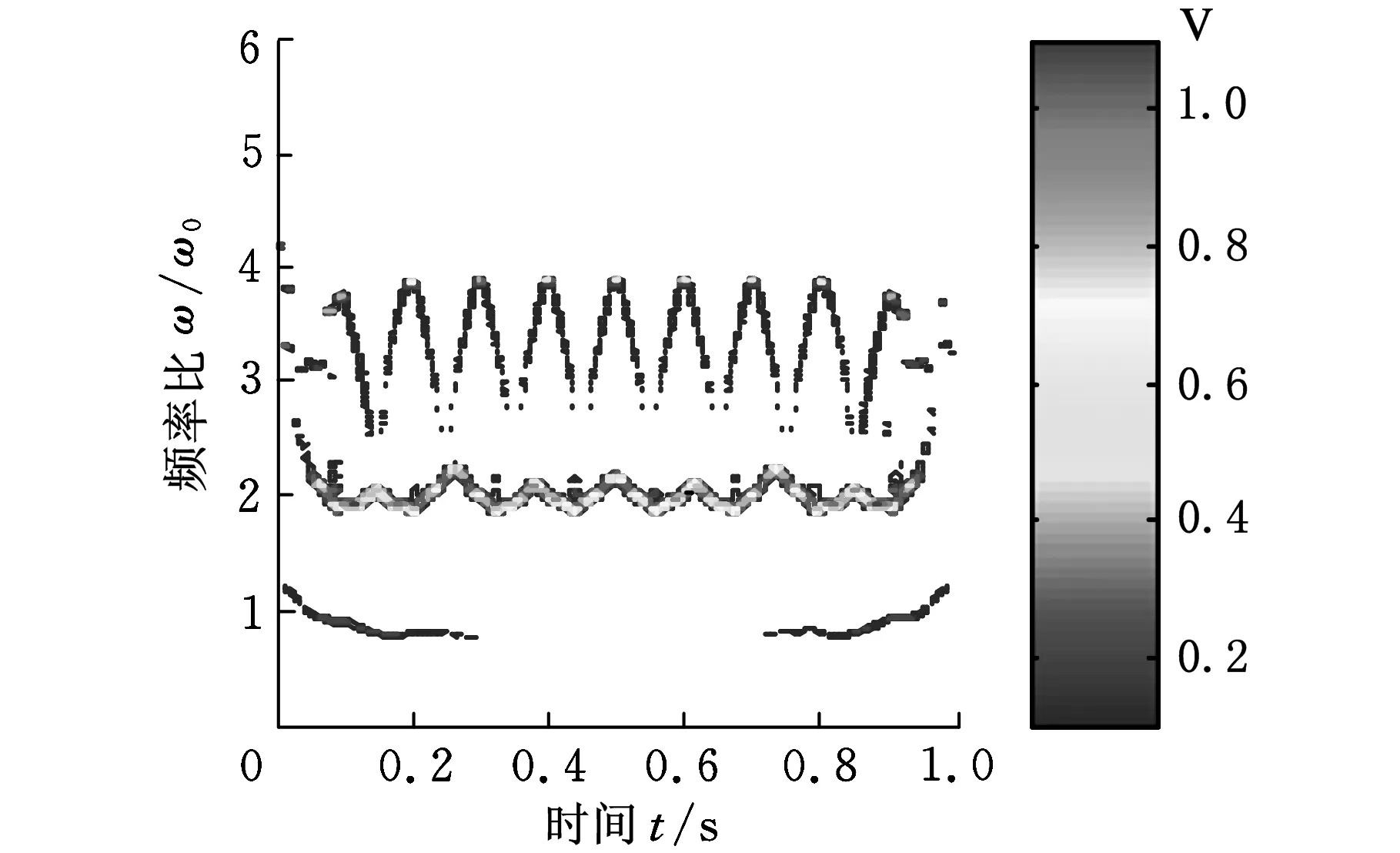
(b)时频谱图7　未延拓EMD分解结果与时频谱

(a)EMD分解结果

(b)时频谱图8　神经网络延拓后的EMD分解结果与时频谱

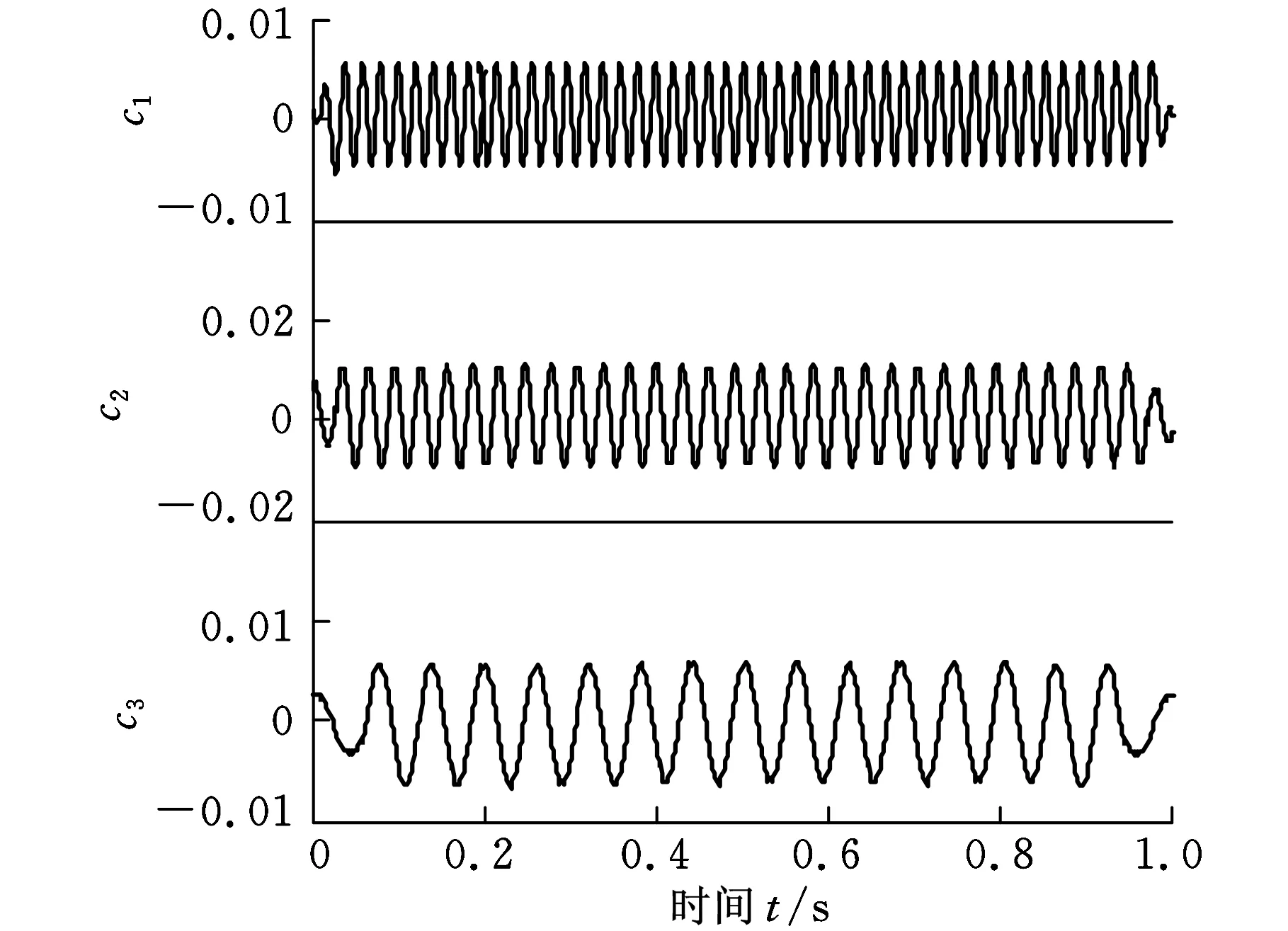
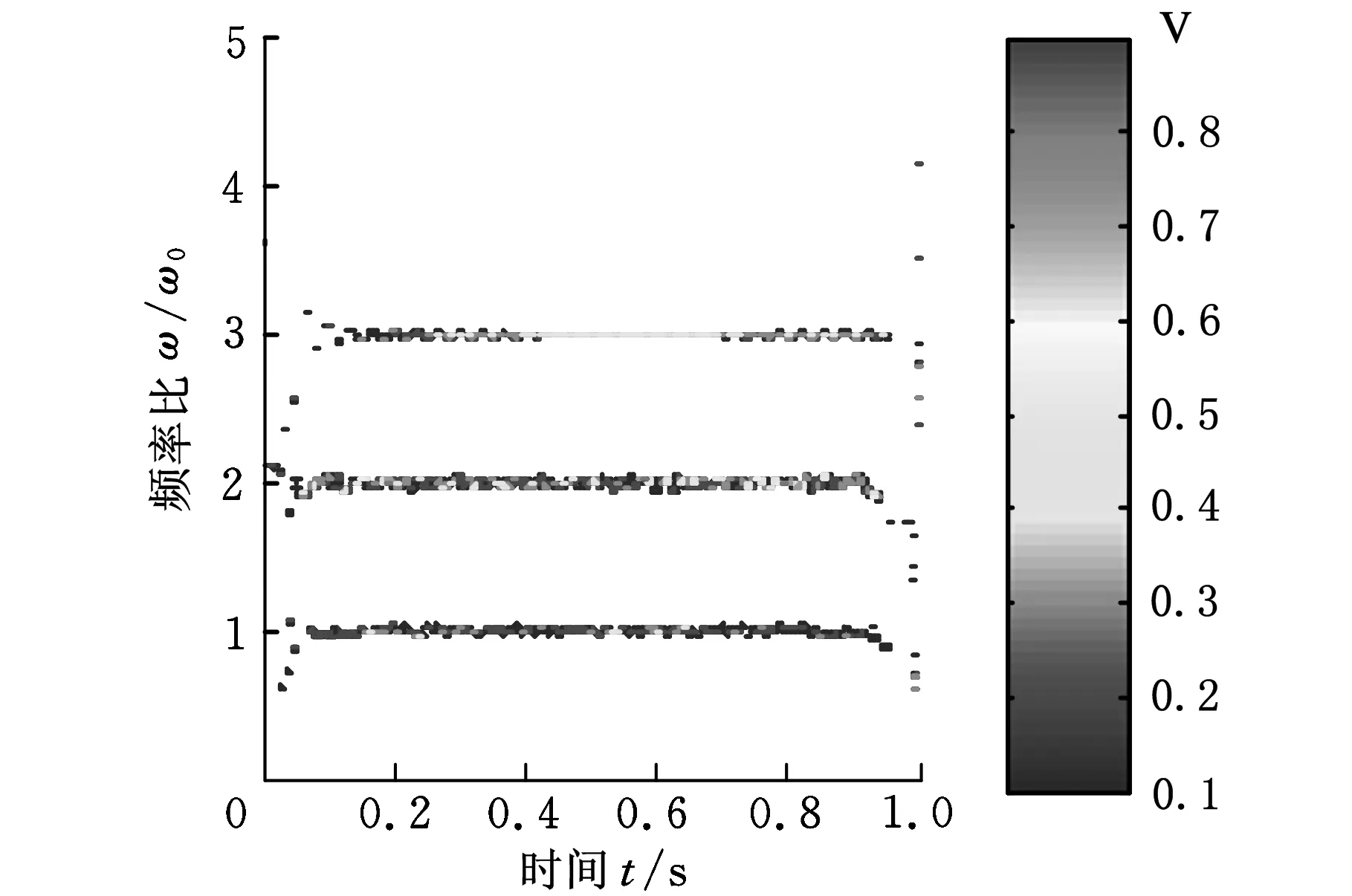
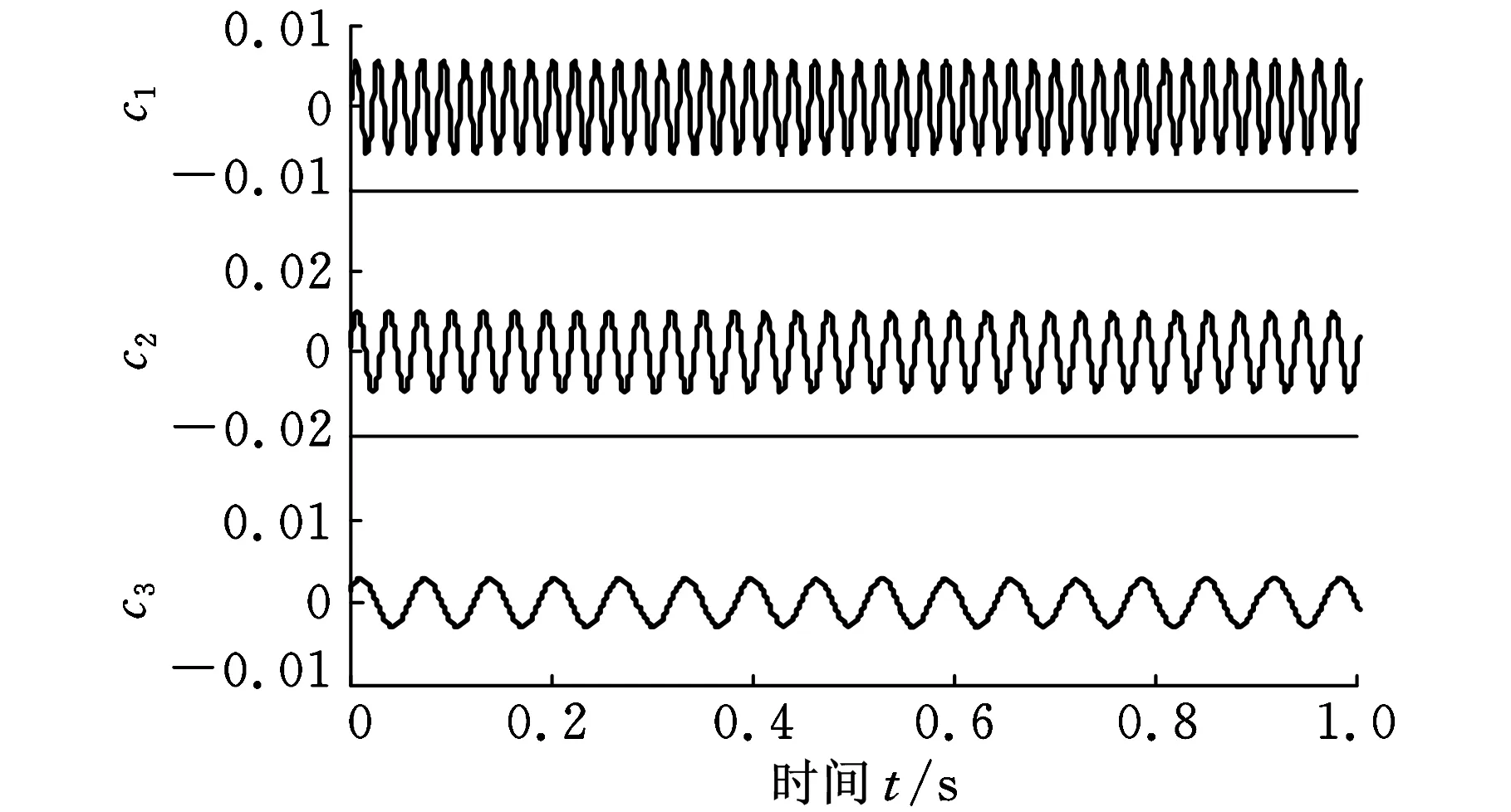
最后利用HMM误差预测方法对神经网络延拓后的数据进行校正后再进行EMD分解得到图9所示的抑制端点效应后的分解效果与时频谱图。图7～图9中选取的IMF分量为EMD分解后的能量较高的前三个IMF分量。

根据转子支撑松动故障机理，振动响应除基频x外还有2x、3x等高频谐波，一定条件下还会产生1/2、1/4等偶分数次谐波共振现象。对比图7～图9发现，未进行延拓的信号的EMD分解端点效应最为明显，分解效果不理想，2倍频与3倍频都不能很好地识别。神经网络进行延拓后，虽然能够分离2倍频与3倍频，但端点效应没有得到明显抑制，给故障诊断带来了一定的困难。用HMM对神经网络延拓进行校正后，分解结果较为理想，且故障特征频率2倍频与3倍频分离较好，能够很好地实现故障识别与诊断。

(a)EMD分解结果

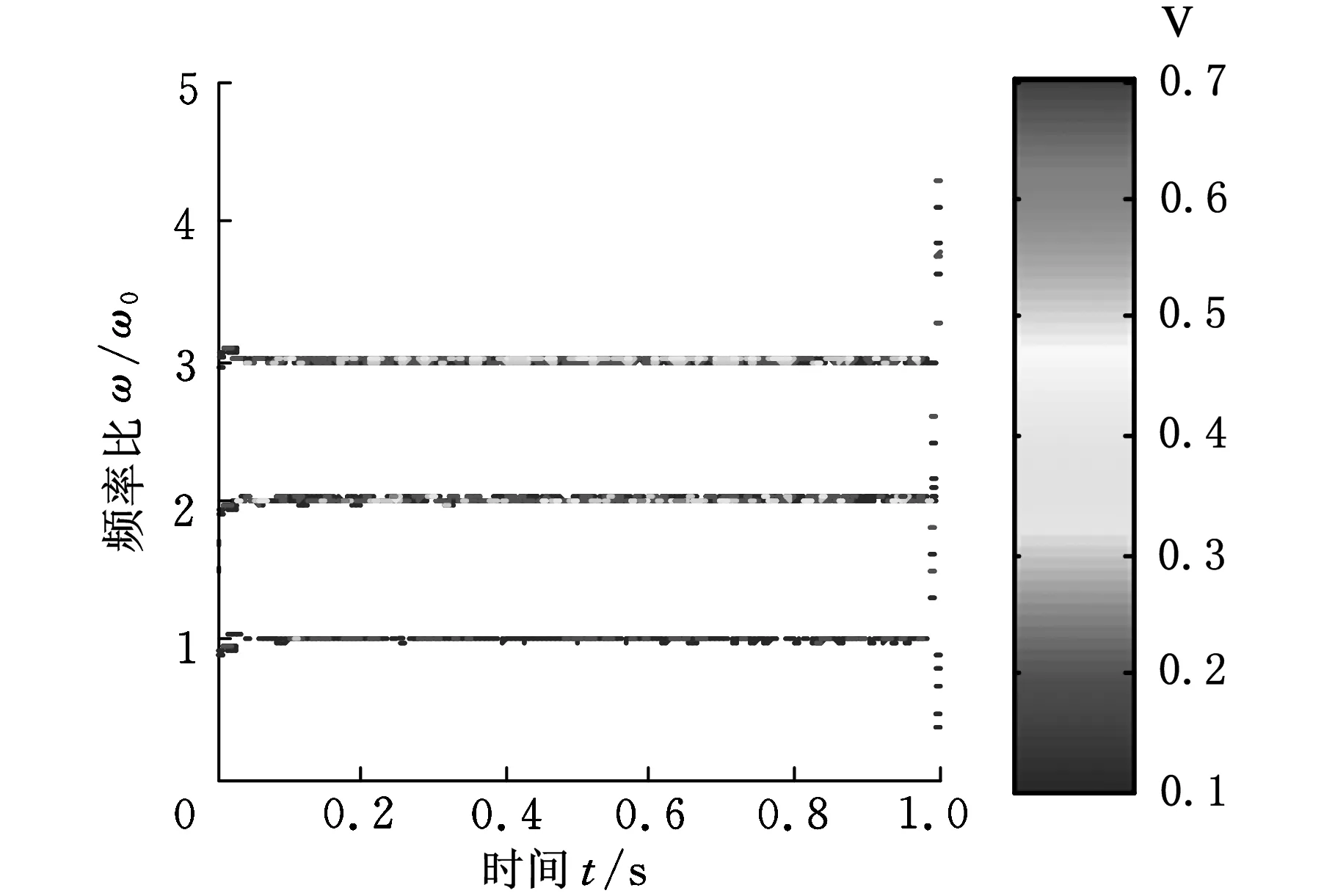
(b)时频谱图9　HMM校正后的EMD分解结果与时频谱图

5　结论

(1)本文在分析EMD端点效应的产生原因和端点效应对EMD分解影响的基础上，将HMM和神经网络集成延拓方法相结合，提出了一种基于HMM校正与神经网络延拓的EMD端点效应抑制方法。

(2)利用RBF神经网络预测估计方法对部分原始数据进行估计，同时对端点外数据进行预测，通过计算估计数据与真实数据的误差序列，利用HMM建立估计误差序列模型，用以预测延拓后数据的误差，得到新的校正后延拓数据。

(3)通过仿真和实验研究验证了本方法抑制端点效应的有效性和可行性。

[1]Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceedings of Royal Society of London A, 1998,454:903-995.

[2]Huang W,Shen Z,Huang N E,et al.Nonlinear Indicial Response of Complex Nonstationary Oscillations as Pulmonary Hypertension Responding to Step Hypoxia[J].Proceedings of the National Academy of Science, USA, 1999,96(5):1834-1839.

[3]杨宇,于德介,程军圣.基于EMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击,2005,24(1): 85-88.

Yang Yu,Yu Dejie,Cheng Junsheng.Roller Bearing Fault Diagnosis Method Based on EMD and Neural Network[J].Journal of Vibration and Shock,2005,24(1): 85-88.

[4]程军圣,于德介,杨宇.基于EMD和分形维数的转子系统故障诊断[J].中国机械工程,2005,16(12):1088-1091.

Cheng Junsheng,Yu Dejie,Yang Yu.Fault Diagnosis for Rotor System Based on EMD and Fractal Dimension[J].China Mechanical Engineering,2005,16(12):1088-1091.

[5]孟宗,李姗姗.基于小波半软阈值和EMD的旋转机械故障诊断[J].中国机械工程, 2013, 24(10): 1279-1283.

Meng Zong,Li Shanshan.Research on Fault Diagnosis for Rotating Machinery Based on Semi-soft Wavelet Threshold and EMD[J].China Mechanical Engineering,2013,24(10): 1279-1283.

[6]陈忠,郑时雄.EMD信号分析方法边缘效应分析[J].数据采集与处理, 2003, 18(1): 114-118.

Chen Zhong,Zheng Shixiong.Analysis on End Effects of EMD Method[J].Journal of Data Acquisition & Processing, 2003,18(1):114-118.

[7]杜陈艳,张瑜锋,杨平.经验模态分解边缘效应抑制方法综述[J].仪器仪表学报,2009,30(1):55-60.

Du Chenyan,Zhang Yufeng,Yang Ping,et al.Approaches for the End Effect Restraint of Empirical Mode Decomposition Algorithm[J].Chinese Journal of Scientific Instrument,2009,30(1):55-60.

[8]胡劲松,杨世锡.EMD方法基于AR模型预测的数据延拓与应用[J].振动、测试与诊断,2007,27(2):116-120.

Hu Jingsong, Yang Shixi.AR Model Prediction-based EMD Method and Its Application to Data Extension[J].Journal of Vibration,Measurement & Diagnosis,2007,27(2):116-120.

[9]韩建平,钱炯,董小军.采用镜像延拓和RBF神经网络处理EMD中端点效应[J].振动、测试与诊断,2010,30(4)：414-417.

Han Jianping,Qian Jiong,Dong Xiaojun.Suppression of End-effect in Empirical Mode Decomposition by Mirror Extension and Radial Basis Function Neural Network Prediction[J].Journal of Vibration,Measurement & Diagnosis,2010,30(4):414-417.

[10]程军圣，于德介，杨宇.基于支持矢量回归机的Hilbert-Huang变换端点效应问题的处理方法[J].机械工程学报,2006,42(4):23-30.

Cheng Junsheng, Yu Dejie, Yang Yu.Process Method for End Effects of Hilbert-Huang Transform Based on Support Vector Regression Machines[J].Chinese Journal of Mechanical Engineering,2006,42(4):23-30.

[11]孟宗,顾海燕,李姗姗.基于神经网络集成的B样条经验模态分解端点效应抑制方法[J].机械工程学报,2013, 49(9): 106-112.

Meng Zong,Gu Haiyan,Li Shanshan.Restraining Method for End Effect of B-spline Empirical Mode Decomposition Based on Neural Network Ensemble[J].Chinese Journal of Mechanical Engineering,2013,49(9): 106-112.

[12]柳新民,刘冠军,邱静.基于HMM-SVM的故障诊断模型及应用[J].仪器仪表学报,2006,27(1):45-48.

Liu Xinmin,Liu Guanjun,Qiu Jing.Hybrid HMM and SVM Approach for Fault Diagnosis[J].Chinese Journal of Scientific Instrument,2006,27(1):45-48.

(编辑陈勇)

Restraining Method of End Effect for EDM Based on Error Calibration by HMM and Neural Network

Meng Zong1,2Yan Xiaoli1Wang Sai3

1.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.National Engineering Research Center for Equipment and Technology of Cold Rolling Strip,Qinhuangdao,Hebei,066004 3.R&D Center of Great Wall Motor Company(Automotive Engineering Technical Center of Hebei),Baoding,Hebei,071000

End effects reduced the precision of EMD greatly, and neural network extension was used to restrain the end effects. However, there were forecast errors in the data forecasted by neural network. Here, a new method, error calibration by HMM was proposed to solve the problem. The radial basis function(RBF) neural network was firstly used to forecast outboard of both ends and estimation part of original signals. Then HMM was used to analyze the forecasting errors and to find the regularity of forecast errors of neural network. According to the analysis, the forecasting errors in next step were analyzed and forecasted to adjust neural network’s forecasting results. Simulation and experiments prove that the method can solve the end effects effectively.

hidden Markov model(HMM); error calibration; neural network; end effect; empirical mode decomposition (EMD)

2014-04-25

国家自然科学基金资助项目(51105323)；河北省自然科学基金资助项目(E2015203356)；河北省高等学校科学研究计划资助重点项目(ZD2015049)

TN911.7；TH165DOI：10.3969/j.issn.1004-132X.2015.14.014

孟宗，男，1977年生。燕山大学电气工程学院教授。主要研究方向为机械设备监测与故障诊断、动力学建模、信号检测与处理等。发表论文20余篇。闫晓丽，女，1986年生。燕山大学电气工程学院硕士研究生。王赛，男，1987年生。长城汽车股份有限公司技术中心(河北省汽车工程技术研究中心)工程师。