金属橡胶非线性隔振系统混沌特性

李玉龙　白鸿柏　何忠波　曹凤利　路纯红

军械工程学院,石家庄,050003



金属橡胶非线性隔振系统混沌特性

李玉龙白鸿柏何忠波曹凤利路纯红

军械工程学院,石家庄,050003

对金属橡胶非线性隔振系统的混沌特性进行了研究。推导了系统振动的状态方程，计算了系统的Lyapunov指数，并根据给定的参数绘制了系统的时间历程图、相轨迹图，证明了系统存在混沌运动。通过系统响应频谱图的分析,说明了金属橡胶非线性混沌振动在线谱控制中的重要作用。用数值方法分析了激励参数与隔振器参数对金属橡胶隔振系统动力学特性的影响，依据系统随各参数变化的分岔图，指出了系统产生混沌运动时各参数的取值范围，从而得到了金属橡胶非线性隔振系统产生混沌振动时各参数选取的一般方法，为金属橡胶非线性隔振系统的混沌特性应用打下了基础。

金属橡胶;非线性隔振系统;李雅普诺夫指数;动力学特性;混沌

0　引言

金属橡胶是一种具有重要工程应用价值的新兴材料,被广泛应用于航空航天、汽车、船舰等工业领域,对延长设备的寿命、提高可靠性有较大的作用[1]。

金属橡胶隔振系统是一个典型的具有迟滞非线性性能的系统,在工程中的应用表现出明显的非线性动力学特性，但金属橡胶非线性隔振系统能否产生混沌响应，其产生混沌响应的参数条件怎样确定,是本文试图研究的问题。目前对金属橡胶非线性隔振系统混沌响应特性的研究成果很少,文献[2]通过数学方法推导了金属橡胶隔振系统产生混沌的解析条件,但该推导建立在预设系统的一次谐波解上,而非线性系统的响应却存在多谐波频率成分[3],仅用一次谐波解来分析系统混沌容易产生较大的误差。尽管对金属橡胶隔振系统混沌振动的研究成果很少，但对非线性隔振系统的混沌研究已有许多成熟的理论可以借鉴。例如,金俐等[4]针对非光滑动力系统,研究了Lyapunov指数谱的计算方法,为lyapunov指数判定混沌运动打下了理论基础;叶建军等[5]研究了含二次项和三次项的非线性系统的次谐轨道和异宿轨道;楼京俊等[6]研究了多频激励软弹簧型Duffing系统中的混沌运动;李鸿光等[7]研究了带间隙的双线滞回系统的非线性振动;唐果等[8]从理论上研究了单自由度被动隔振体产生混沌的参数条件;牛玉俊等[9]研究了非光滑周期扰动与有界噪声联合作用下受迫Duffing系统的混沌预测；刘树勇等[10]对准周期激励下的非线性隔振系统进行研究,应用Melnikov方法确定了系统的参数区域;Yu等[11]研究了多自由度非线性隔振系统的混沌及分岔;浣石等[12]用数值计算的方法证明了随着系统从周期分岔逐渐进入混沌运动状态，线谱也由单一频谱变为宽频谱结构;黄志伟等[13]采用数值积分法分析了双层隔振系统产生混沌运动的频率范围。从上述对非线性隔振系统的混沌研究成果可以看出，对非线性隔振系统混沌的研究主要是通过理论或数值的方法展开分析,主要针对产生混沌运动的条件进行讨论,以得到非线性系统产生混沌的判据及其激励参数或隔振器参数的选取范围。许多文献指出，混沌状态下系统的振动具有单频输入宽频输出的特性，可以大幅度隔离结构噪声中的线谱成分，在消除线谱激励方面具有明显的优势，对提高船舰的隐身性能具有重要的意义[12-14]，因此，在船舰减声降噪技术研究领域，诸多学者对非线性系统混沌特性进行了研究。

本文针对单自由度金属橡胶非线性隔振系统的动力学特性展开研究。

1　金属橡胶非线性隔振系统模型

金属橡胶材料具有良好的可塑性，可以根据工程需要制备成不同形状的元件,因此,金属橡胶隔振器的种类也多种多样[15]。但本文只针对图1a所示的单自由度隔振器结构组成的隔振系统展开研究,这类系统结构简单，但最具有代表性，是研究金属橡胶隔振系统混沌振动的最基本类型。

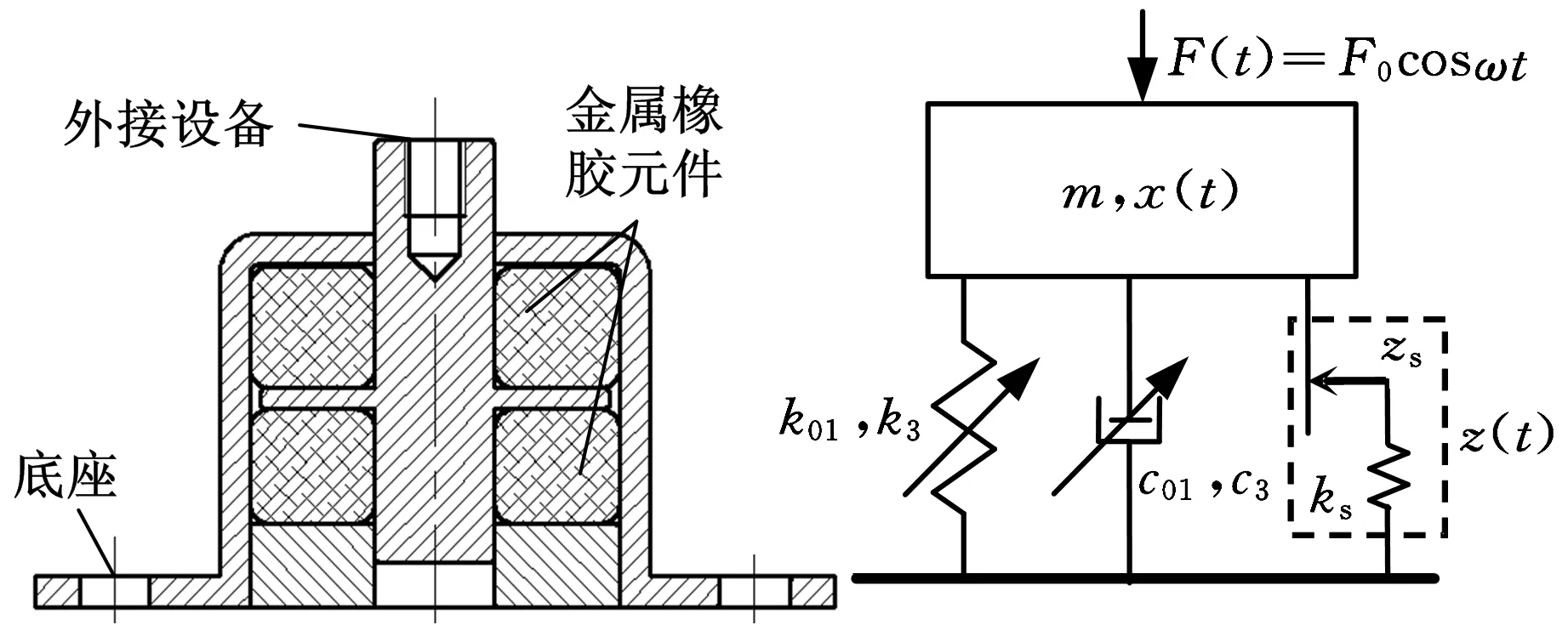
(a)隔振器(b)力学模型图1　单自由度金属橡胶隔振器及其系统力学模型

对于单自由度金属橡胶隔振系统，一般作以下假设:①刚性设备被单向金属橡胶隔振器支撑;②仅有垂直方向的单个自由度的振动，且激励为作用在刚性设备质心的简谐激励F(t)=F0cosωt(F0为激励幅值,ω为激励频率,t为时间)。因此，可将系统简化为一个单自由度的简单模型,如图1b所示。

图1b中，m为被隔振设备的质量；x(t)为设备随时间变化的位移，与在刚性基础上隔振器的变形量相等；金属橡胶隔振器有明显的迟滞非线性特性，其本构关系为

(1)

其中,G(t)为隔振器的恢复力,k01为一次线性刚度系数,k3为三次非线性刚度系数,c01为黏弹阻尼系数,c3为三次非线性黏弹阻尼系数，它们形成与位移有关的弹性力和与速度有关的黏性阻尼力,通常被认为是无记忆恢复力；z(t)是金属橡胶变形过程中干摩擦引起的记忆恢复力,由于该记忆恢复力的存在,金属橡胶隔振系统一般表现出明显的滞后非线性性能,其中,zs表示滑移极限,ks表示滑移刚度,且有ks=zs/xs,xs是开始滑移时的变形量。将记忆恢复力用双折线模型表示[16],如图2所示。

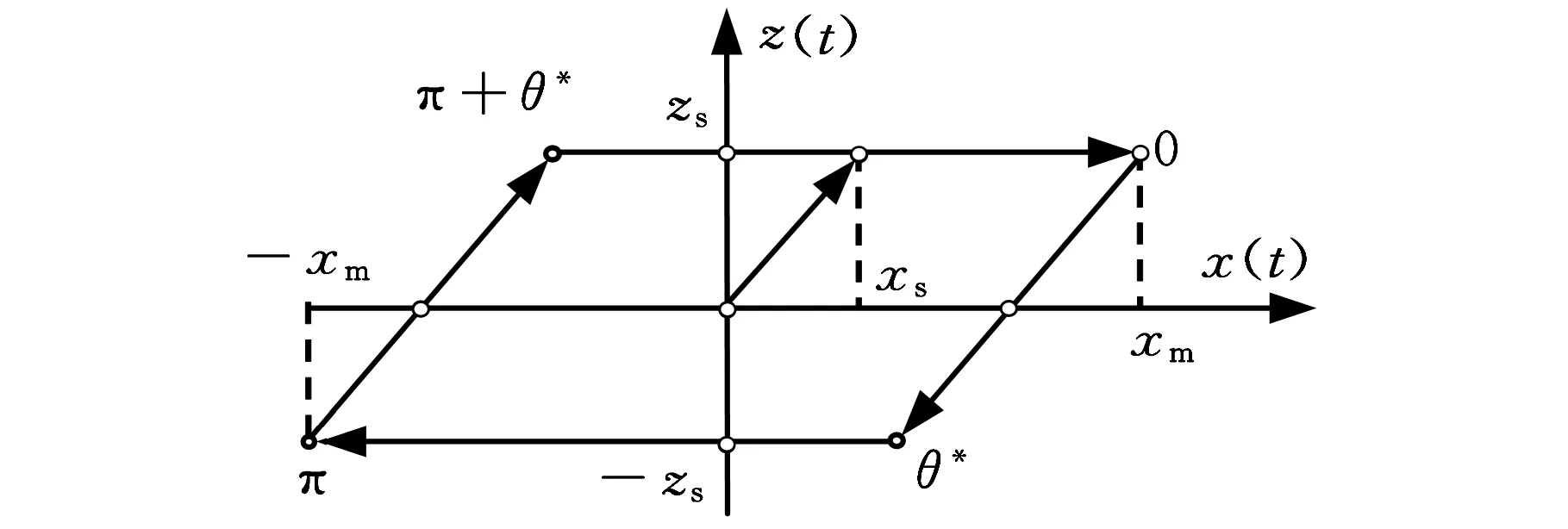
图2　双折线迟滞关系模型

图2中,xm是最大变形量。为了简化分析,用等效线性化法对干摩擦滞迟环节进行等效线性化，可得

(2)

将记忆环节进行线性等效,即包含变化的线性刚度项keq和变化的黏性阻尼项ceq,则金属橡胶隔振器在隔振系统中的本构关系可表示为

(3)

令k1=k01+keq,c1=c01+ceq,并假设隔振器的质量很小,可以忽略不计,则图1b所示的单自由度金属橡胶非线性隔振系统的微分方程可写成

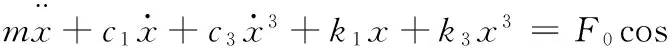
(4)

化简式(4),得

(5)

2　Lyapunov指数判定系统的混沌振动

由于混沌运动对系统的初始条件具有敏感性,即使原来相互之间比较接近的两条相轨迹,它们之间的距离也会随着时间的增加而变得越来越大。因此，可以用能够刻画这种相邻相轨迹逐渐远离特征的数值来识别系统的混沌运动。Lyapunov指数能够描述系统相邻相轨迹之间距离的发散性。为判定金属橡胶非线性隔振系统的混沌运动，本文首先计算系统的Lyapunov指数[6],以判定系统能否产生混沌振动。

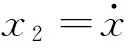
(6)

(7)

则由式(7)可确定一个三维非自治系统，即

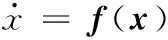
(8)

其中,x=[x1x2x3]T是三维状态变量。给定两条相轨迹，它们对应的初始条件分别是x0和x0+Δx0,Δx0为初始条件的微小差异。则在某一时刻t,两条相邻相轨迹之间的距离可以用变分‖δx‖来表示，即

δx=x(x0+Δx0,t)-x(x0,t)

(9)

将式(8)在x0处线性化,得

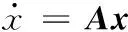
(10)

其中,常数矩阵A是3×3雅可比矩阵，其元素ai j为

(11)

可得

(12)

将得到的δx表示成线性方程:

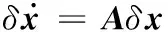
(13)

式(13)的解为

δx=δx0eλ t

(14)

式(14)两端取范数后,再取自然对数得到Lyapunov表达式：

(15)

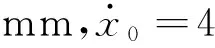
基于以上预设的参数,采用四阶龙格-库塔法求解式(6),可得被隔振设备的位移时间历程(即系统的响应)图和相轨迹,分别如图3、图4所示。

图3　位移时间历程

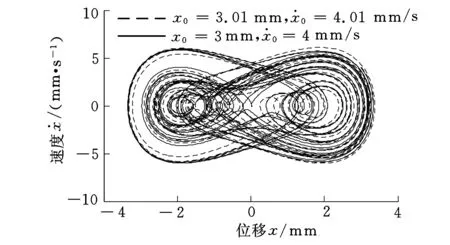
图4　相轨迹

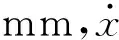
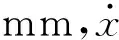
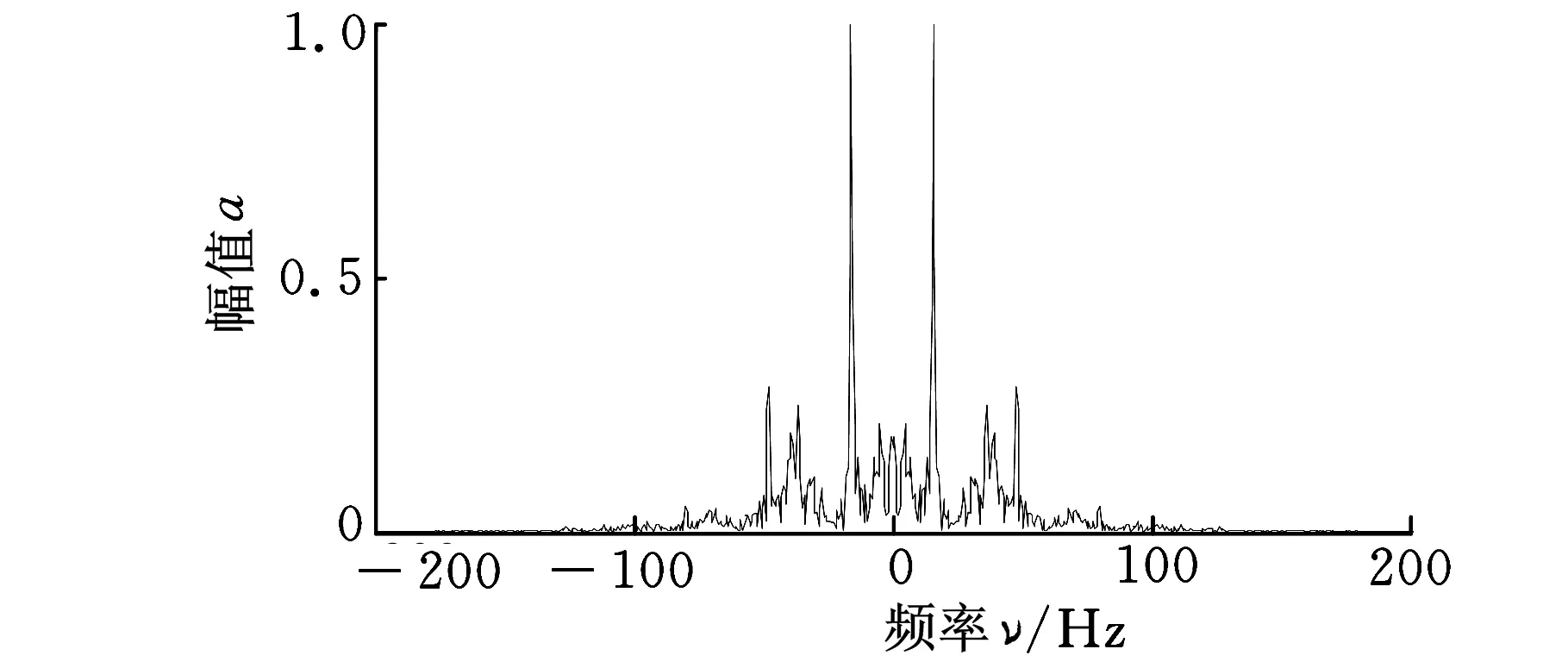
图5　频谱图

由于被动声呐在现代水声对抗中发现、跟踪和识别水下装备的主要特征和水下装备声隐身性能的主要考核指标就是结构振动的线谱，故改变水下装备的线谱成分，使其转化为类似于随机振动的线谱成分，以提高在传播过程中的衰减程度，增大声呐探测难度是国内外学者的研究热点。而本节证明金属橡胶非线性隔振系统具有混沌响应特性，使金属橡胶在舰艇等水下设备及其他需要控制系统线谱的特殊装备的减声降噪技术领域具有重要的推广应用价值。

3　激励及系统参数对系统的动力学影响

由于系统产生混沌的本质是系统输入项和耗散相互竞争的结果[12],故在系统混沌振动产生与否应视激励和隔振器的参数而定：即在一定的激励环境下,要使系统产生混沌就必须选择合适的非线性隔振系统参数；对于一定的非线性隔振系统,要使系统产生混沌响应就必须调整激励的频率或幅值。因此，需要对激励参数及隔振器参数对系统的动力学影响展开讨论。

3.1激励频率与幅值对系统动力学特性的影响

简谐激励通常用激励和幅值两个参数来表示，而一般的非简谐激励也可以通过Fourier级数展开后用多个谐波成分叠加来近似表示。因此，本文主要讨论简谐激励的幅值和频率对金属橡胶非线性隔振系统动力学特性的影响。

由于上节已经证明，在预设的参数下已经确定系统发生混沌振动,故可按上节参量数值分别给定其他参数，再单独研究激励频率ω或激励幅值参量f的变化对系统动力学特性的影响,并结合式(7)讨论激励实际的频率和幅值的影响。采用数值方法分别绘制系统随激励频率和幅值变化的分岔图,如图6、图7所示。

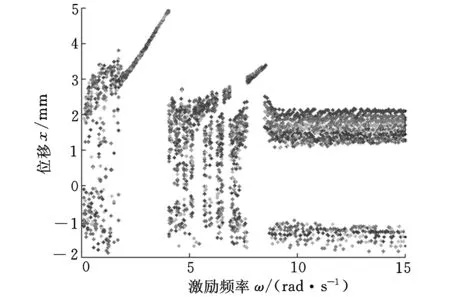
图6　系统随激励频率变化的分岔图

图7　系统随激励力幅值变化的分岔图

从图6可以看出，激励频率ω在0～15 rad/s,Δω=0.1 rad/s范围内出现多次分岔现象，且在不同频率段有不同的响应特性：在2～4.5 rad/s,7.6～8.2 rad/s范围内只存在周期振动,而在0～2 rad/s,4.2～7.5 rad/s范围内出现混沌现象,8.2 rad/s以上出现多种周期成分的振动现象。从图7也可以看出,系统随激励幅值参量(f=F0/m)在0～10,Δf=0.1范围内,出现多次分岔:在0～4.6范围内只存在周期振动或多种倍周期振动，在4.6～8.5范围内出现混沌现象，在8.5以上存在多种周期振动。

可见,对于已定的金属橡胶非线性系统，激励的频率和幅值只有在某一较小的范围内产生混沌振动。因此，在利用系统混沌状态进行隔振时，应当首先通过数值仿真计算，确定激励参数的大概范围，然后进行多次试验，挑选合适的激励幅值和频率，使系统处于混沌状态。

3.2隔振器参数对系统动力学特性影响

在某一指定的环境下(激励一定)，其激励的频率和幅值已经固定，如果利用金属橡胶隔振器进行隔振，则需要讨论隔振器参数对系统动力学特性的影响。按照以上分析，同理可分别单独讨论隔振器一次刚度、三次刚度，一次阻尼和三次阻尼的变化对系统动力学特性的影响。结合式(7)分别调整参数范围，利用数值方法绘制系统随各参数变化的分岔图，如图8～图11所示。在每讨论完一个量纲一系数产生混沌的最优取值后,讨论下一个参数时预先设定的参数取值根据讨论过的最优取值而重新设定。

图8　系统随ξ1变化的分岔图

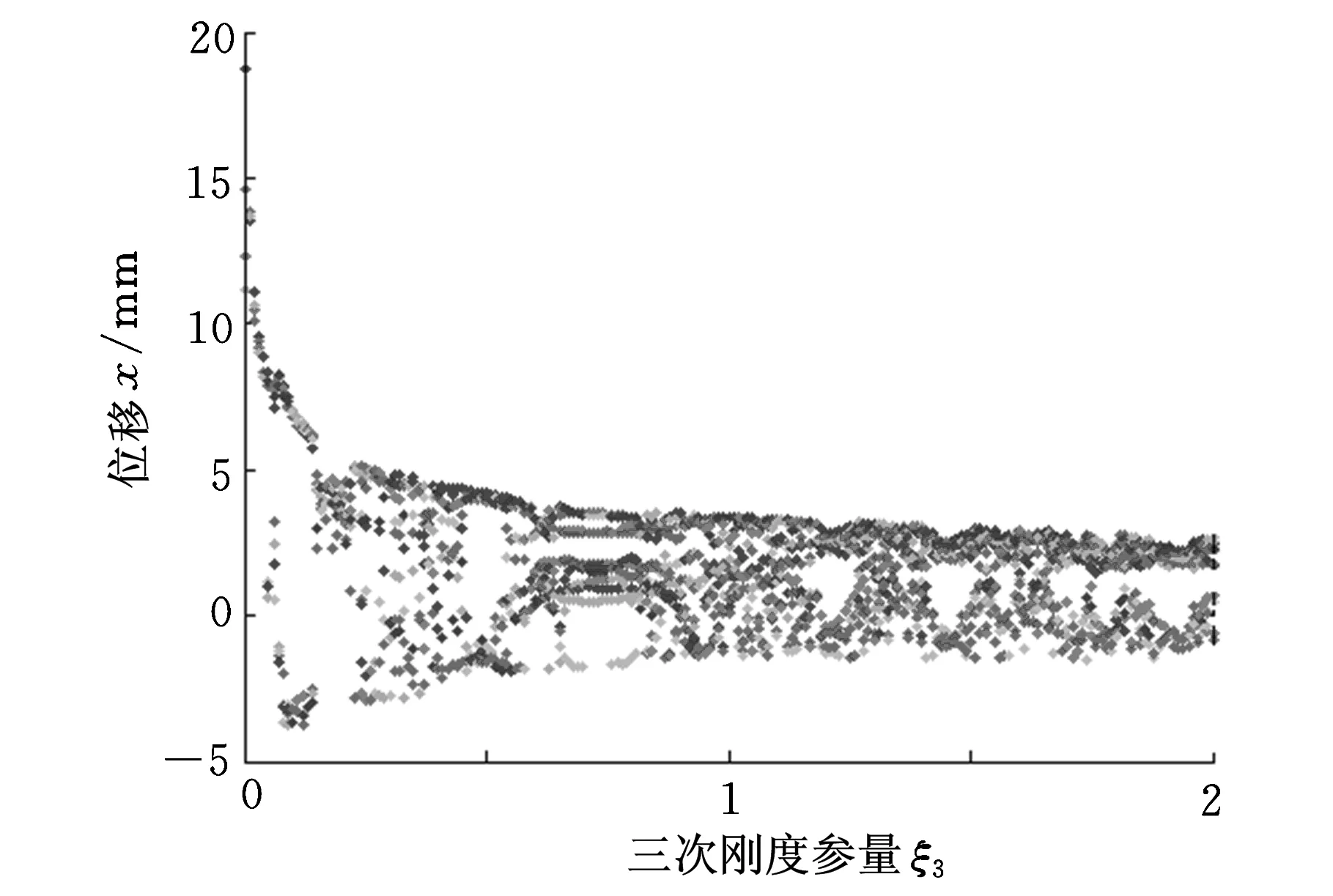
图9　系统随ξ3变化的分岔图

从图8、图9可以看出，对于一次刚度参量ξ1(ξ1=k1/m),当f=7.5,ω=4.8 rad/s,ξ3=1,μ1=0.05,μ3=0.001时,ξ1取0～0.1,Δξ1=0.0001数值范围内，系统响应产生多次分岔，出现了周期、多种倍周期振动，且在ξ1取0.05～0.063范围内的值时系统产生混沌现象；对于三次刚度参量ξ3(ξ3=k3/m),当f=7.5,ω=4.8，ξ1=0.055,μ1=0.05,μ3=0.001时,ξ3取0～0.1,Δξ3=0.001数值范围内,系统响应产生多次分岔，出现了周期、多种倍周期振动，且在ξ3取0.25～0.45、0.85～1.15、1.3～1.42等范围内的值时系统产生混沌现象。

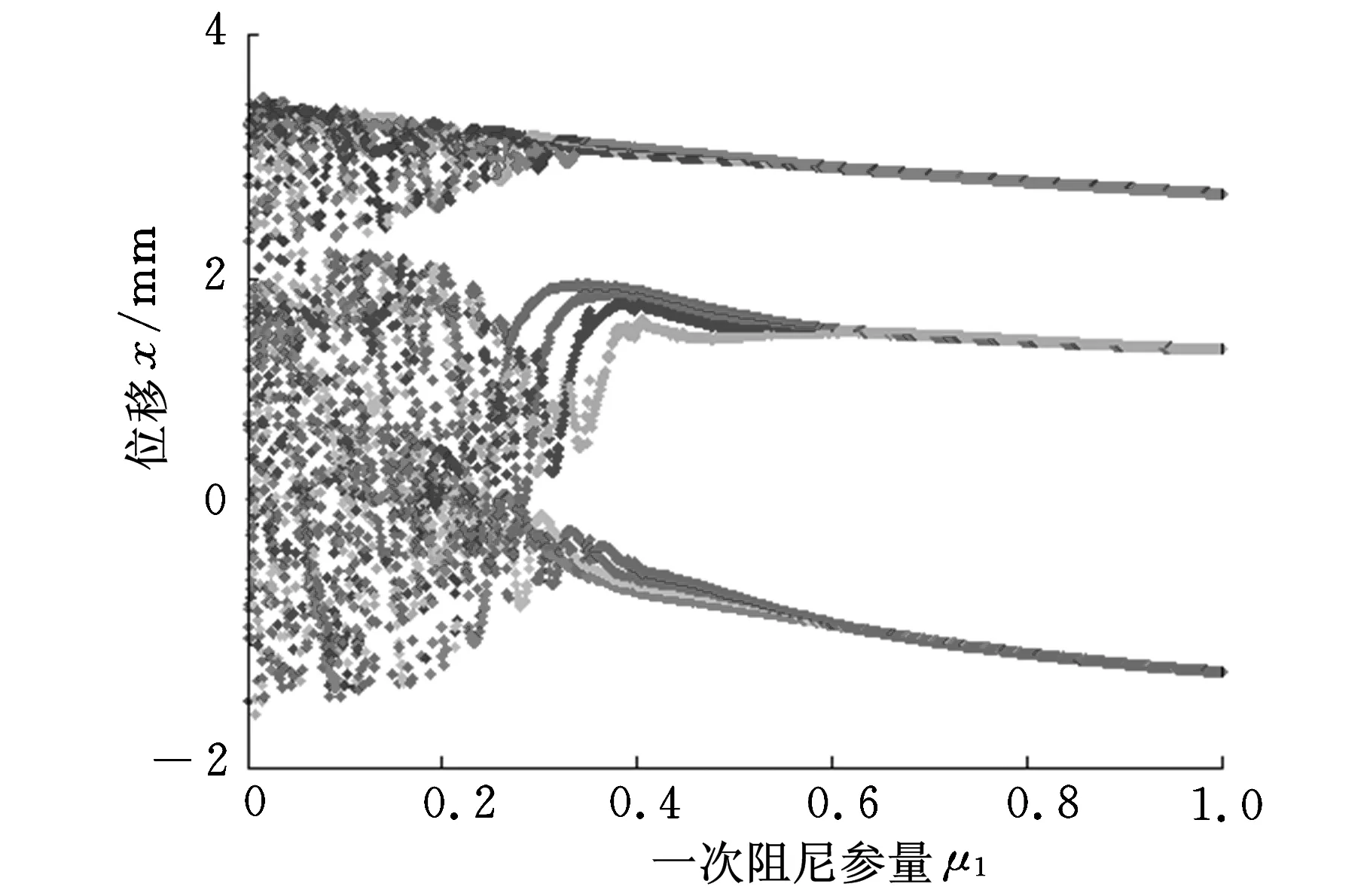
图10　系统随μ1变化的分岔图

图11　系统随μ3变化的分岔图

从图10、图11可知，当f=7.5，ω=4.8 rad/s,ξ1=0.055,ξ3=1，一次阻尼参量(三次阻尼参量)μ1(μ1=c1/m)和三次阻尼参量μ3(μ3=c3/m)仅在较小的数值范围内(μ1<0.3,μ3<0.012)产生分岔和混沌现象，在取较大的数值时，系统为周期振动，且可以看出，一次阻尼参量和三次阻尼参量越小,系统响应分岔越明显，因此，为使系统进入混沌运动状态，应该减小隔振器的阻尼。

由于图8～图11中讨论的参数均为相对应的隔振器物理参数与被隔振设备质量的比值，对于固定质量的被隔振对象，隔振器的实际物理参数仅需要根据式(7)换算即可获得；若被隔振设备质量可以调节，隔振器的参数整体有所偏差，难以找到合适的产生混沌的参数区间时，改变隔振器质量(增加配重质量或减小设备质量)也可能使系统进入混沌振动状态。

4　结语

本文对金属橡胶非线性隔振系统的混沌响应特性进行了研究。首先，计算了给定激励参数、隔振器参数和初值情况下系统的Lyapunov指数，由于指数中存在正值，证明了在给定的参数和初值条件下，系统产生混沌运动，并用龙格-库塔法计算了系统初值微动时响应的时间历程曲线和相轨迹图，通过对比进一步说明了系统处于混沌运动状态。然后对时间历程图进行Fourier变换得到了系统响应的频谱图，频谱图中频率成分的连续性，证明了其单频输入宽频输出的特性,说明了金属橡胶非线性隔振系统混沌振动对线谱控制的有效性。最后重点讨论了激励频率、激励幅值、隔振器一次刚度、三次刚度、一次阻尼和三次阻尼对系统的动力学特性影响,绘制了系统响应随各参数变化的分岔图，从分岔图可以看出，系统产生混沌运动时的参数取值范围，为金属橡胶非线性隔振系统的混沌应用提供了理论指导。

[1]李玉龙,何忠波,白鸿柏,等.金属橡胶的研究及应用研究[J].兵器材料科学与工程,2011,34(1):103-108.

Li Yulong,He Zhongbo,Bai Hongbai,et al.Advance in Research and Application of Metal Rubber[J].Ordnance Material Science and Engineering,2011,34(1):103-108.

[2]唐果,陈安华,郭源君.金属橡胶隔振器产生混沌的解析预测[J].航空动力学报,2012,27(8):1752-1757.

Tang Guo,Chen Anhua,Guo Yuanjun.Chaotic Prediction of Metal Rubber Damper for Occurred Chaos[J].Journal of Aerospace Power,2012,27(8):1752-1757.

[3]徐道临,吕永建,周加喜,等.非线性隔振系统动力学特性分析的FFT多谐波平衡法[J].振动与冲击,2012,31(22):39-44.Xu Daolin,Lü Yongjian,Zhou Jiaxi,et al.FFT Multi-harmonic Balance Method for Dynamic Analysis of a Nonlinear Vibration Isolation System[J].Journal Vibration and Shock,2012,31(22):39-44.

[4]金俐,陆启韶.非光滑动力系统Lyapunov指数谱的计算方法[J].力学学报,2005,37(1):40-47.

Jin Li,Lu Qishao.A Method for Calculating the Spectrum of Lyapunov Exponents of Non-smooth Dynamical Systems[J].Acta Mechanica Sinica,2005,37(1):40-47.

[5]叶建军,陈虬.一类非线性振动系统的混沌运动[J].西南交通大学学报,2001,36(6):629-632.

Ye Jianjun,Chen Qiu.Chaotic Motions in Nonlinear Vibration Systems[J].Journal of Southwest Jiaotong University,2001,36(6):629-632.

[6]楼京俊,何其伟,朱石坚.多频激励软弹簧型Duffing系统中的混沌[J].应用力学和数学,2004,25(12):300-400.

Lou Jingjun,He Qiwei,Zhu Shijian.Chaos in the Softening Duffing System under Multi-frequency Periodic Forces[J].Applied Mathematics and Mechanics,2004,25(12):300-400.

[7]李鸿光,孟光,闻邦春.带间隙的双线滞回系统的非线性振动[J].机械工程学报,2004,40(7):10-13.

Li Hongguang,Meng Guang,Wen Bangchun.Nonlinear Oscillation of Bilinear Hysteretic System with Clearance[J].Chinese Journal of Mechanical Engineering,2004,40(7):10-13.

[8]唐果,陈安华,郭源君.被动隔振体产生混沌的参数条件研究[J].振动与冲击,2010,29(8):35-39.

Tang Guo,Chen Anhua,Guo Yuanjun.Parametrical Condition for Chaos Occurrence on a Vibration-isolated Body[J].Journal of Vibration and Shock,2010,29(8):35-39.

[9]牛玉俊,徐伟,戎海武.非光滑周期扰动与有界噪声联合作用下受迫Duffing系统的混沌预测[J].物理学报,2008,57(12):7535- 7540.

Niu Yujun,Xu Wei,Rong Haiwu.Chaos Perdiction in the Duffing-type System with Non-smooth Eriodic Perturbation and Bounded Parametric Excitation[J].Acta Physica Sinica,2008,57(12):7535-7540.

[10]刘树勇,朱石坚,俞翔.准周期激励非线性隔振系统的混沌研究[J].船舶力学,2010,14(2):141-147.

Liu Shuyong,Zhu Shijian,Yu Xiang.Study on the Chaos of the Nonlinear Vibration Isolation System under Quasi-periodic Excitation[J].Journal of Ship Mechanics,2010,14(2):141-147.

[11]Yu Xiang, Zhu Shijian, Liu Shuyong.Bifurcation and Chaos in Multi-degree-of-freedom Nonlinear Vibration Isolation System[J].Chaos, Solitons& Fractals,2008,385(5):1498-1504.

[12]浣石,陶为俊,朱石坚,等.硬特性隔振装置混动动力学特性研究[J].振动与冲击,2011,30(1):245-248.

Huan Shi,Tao Weijun,Zhu Shijian,et al.Chaotic Dynamic of Harding Nonlinear Isolation Device[J].Journal of Vibration and Shock,2011,30(1):245-248.

[13]黄志伟,何雪松,陈志刚,等.非线性隔振系统振动特性分析[J].动力学与控制学报,2013,11(3):252-256.

Huang Zhiwei,He Xuesong,Chen Zhigang,et al.Research on the Vibration Characteristics of Nonlinear Isolation System[J].Journal of Dynamics and Control,2013,11(3):252-256.

[14]张振海,朱石坚,何其伟.基于反馈混沌化方法的多线谱控制技术研究[J].振动工程学报,2012,25(1):30-37.

Zhang Zhenhai,Zhu Shijian,He Qiwei.Multi-line Spectra Reduction of Vibration Isolation System Based on Chaotification Method[J].Journal of Vibration Engineering,2012,25(1):30-37.

[15]白鸿柏,路纯红,曹凤利,等.金属橡胶材料及工程应用[M].北京:科学出版社,2014.

[16]白鸿柏,张培林,郑坚,等.迟滞振动系统及其工程应用[M].北京:科学出版社,2002.

(编辑陈勇)

Chaotic Characteristics of Nonlinear Metal Rubber Vibration Isolation System

Li YulongBai HongbaiHe ZhongboCao FengliLu Chunhong

Ordnance Engineering College,Shijiazhuang,Hebei,050003

The chaotic characteristic of nonlinear metal rubber vibration isolation system was studied herein.The system state equation was derived,the Lyapunov exponent was calculated,the displacement time history diagram and the phase track diagram were draw out,it proved that the system was in the chaotic state under the conditions of the given parameters.Through the analysis of the system response spectrum diagram,the metal rubber nonlinear vibration isolation system chaos was illustrated in the important role of line-spectrum control.The parameters of the excitation and the vibration isolator’s impacts on system dynamics characteristic were analyzed by using numerical methods.The parameter scopes in the chaotic state were confirmed based on the bifurcation diagram changed with the parameters of the excitation and the vibration isolator.The general selection method of the parameter was got,which could make the system be in the chaotic state,and it lays a foundation for the applications of the nonlinear metal rubber chaotic vibration.

metal rubber;nonlinear vibration-isolation system;Lyapunov exponent;dynamics characteristic;chaos

2014-09-26

武器装备“十二五”预先研究项目(51312060404)

V214.9;TH17;TH113DOI：10.3969/j.issn.1004-132X.2015.14.006

李玉龙,男,1987年生。军械工程学院车辆与电气工程系博士研究生。主要研究方向为振动与冲击防护、金属橡胶材料及其应用、非线性隔振系统动力学。白鸿柏,男,1964年生。军械工程学院车辆与电气工程系教授、博士研究生导师。何忠波,男,1968年生。军械工程学院车辆与电气工程系教授、博士研究生导师。曹凤利,男,1978年生。军械工程学院车辆与电气工程系讲师、博士。路纯红，女，1971年生。军械工程学院车辆与电气工程系副教授、博士。