基于测量不确定度的产品检验中误判率计算
陈晓怀 王汉斌 程银宝 姜 瑞
合肥工业大学,合肥,230009
基于测量不确定度的产品检验中误判率计算
陈晓怀王汉斌程银宝姜瑞
合肥工业大学,合肥,230009
根据ISO14253-1,研究了基于测量不确定度的产品合格判定原理与方法。分析了产品检验中测量不确定度对合格判定的影响,由不确定度的分布函数推导出批量产品检验中误判率的计算公式;分别讨论了测量结果位于不同区间时,单个产品合格判定及误判率的计算方法;编制了基于LabVIEW的合格判定软件,只需输入相关预知参数,即可获得产品合格判定的结果及其误判率。实例分析表明,测量不确定度造成产品检验存在误判,合格判定软件有效提高了不确定度理论在产品检验应用中的可操作性,基于不确定度的误判率计算为产品供求双方协商确定产品的合格性提供了准确可靠的依据。
产品检验;合格判定;测量不确定度;误判率
0 引言
尽管ISO9000系列标准和ISO14253-1等国际标准都明确规定在产品检验时应考虑测量不确定度的影响,但实际中很多企业往往将不确定度理论视为“空中楼阁”。原因是:一方面很多测量仪器在给出测量结果的同时不能直接给出测量不确定度[1];另一方面相关国际标准本身仅仅从总体上给出了产品检验中合格判定的一般原则,对于误判率计算等具体问题缺乏可操作性指导。
针对该问题,国内外学者进行了大量研究[2-11]。综合国内外研究现状可知,当前研究在不确定度评定方法方面已取得丰硕成果,但产品检验中测量不确定度应用的研究则存在诸多局限性,如:大量文献仅限于对ISO14253-1等国际标准内容进行归纳与解读,对于实际产品检验中误判率的计算并未给出有效方法;部分文献虽然研究了误判率的计算问题,但在分析计算时,采用的数学模型中往往用随机误差代替不确定度。因为随机误差只能反映测量过程中随机的、变化的因素对测量结果的影响,用其数学模型代替不确定度的分布规律不够准确。
针对当前研究的局限性,本文首先从总体上论述了测量不确定度对产品质量检验的影响,根据不确定度分布规律推导了批量产品合格判定中误判率计算的数学模型。在此基础上,对单个测量结果的合格判定和误判率计算进行讨论。
1 测量不确定度对产品合格判定的影响
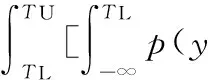
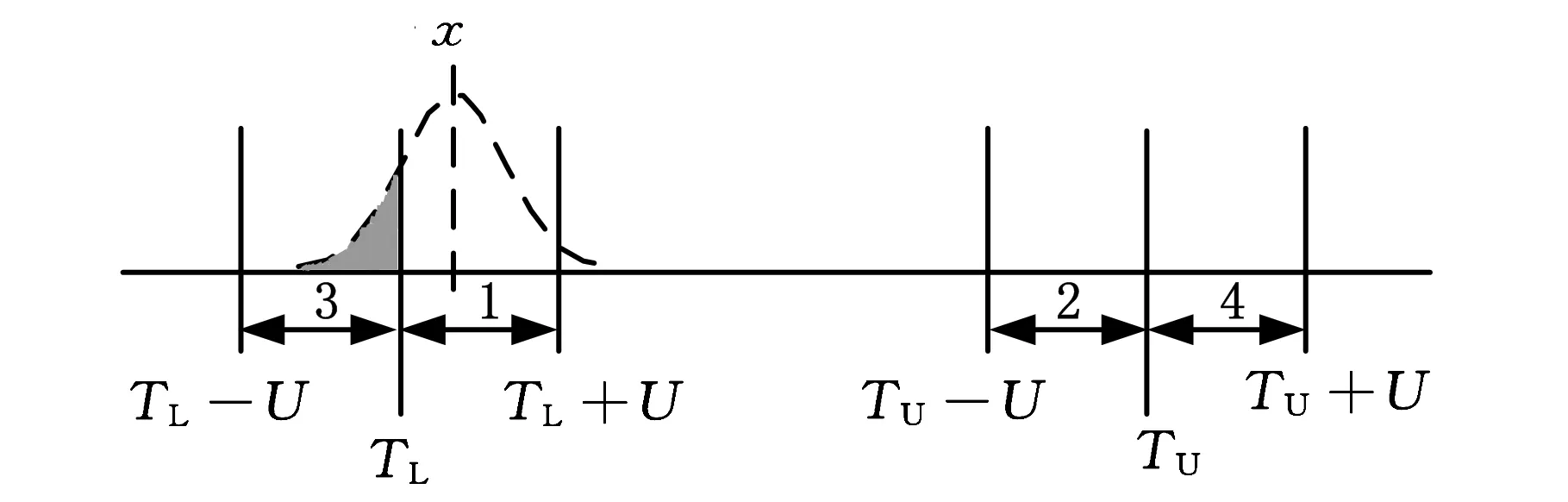
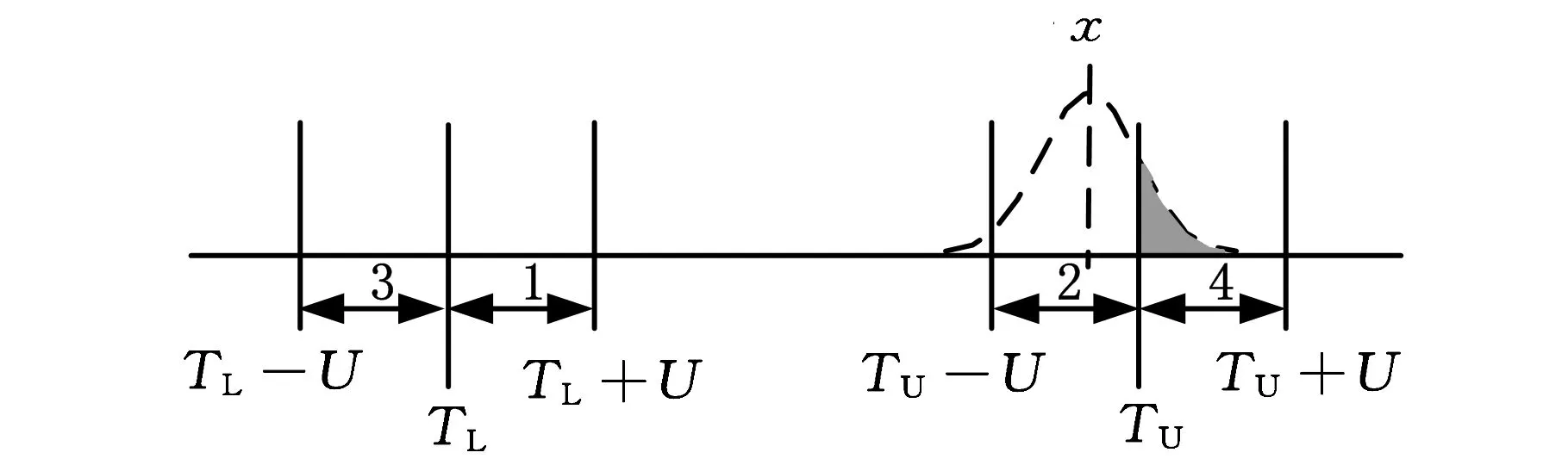
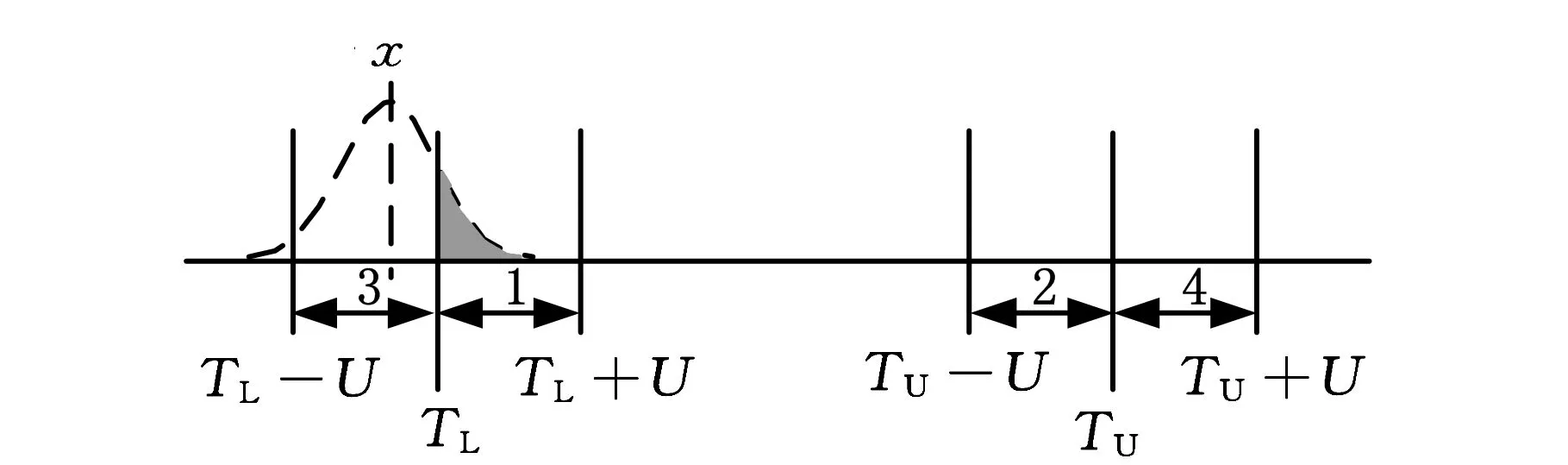
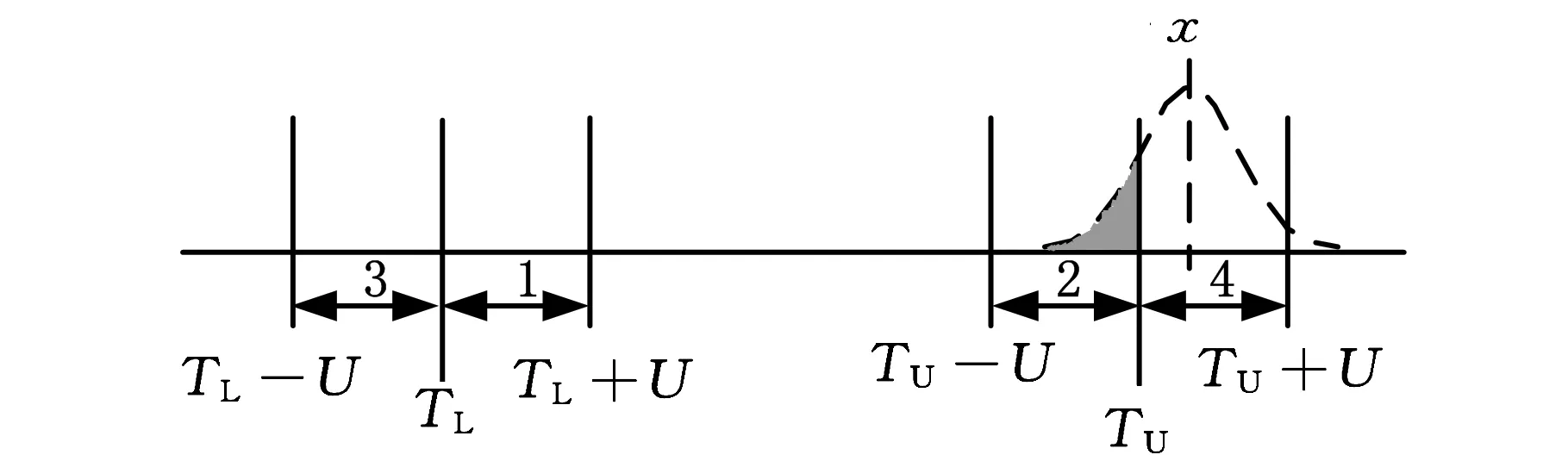
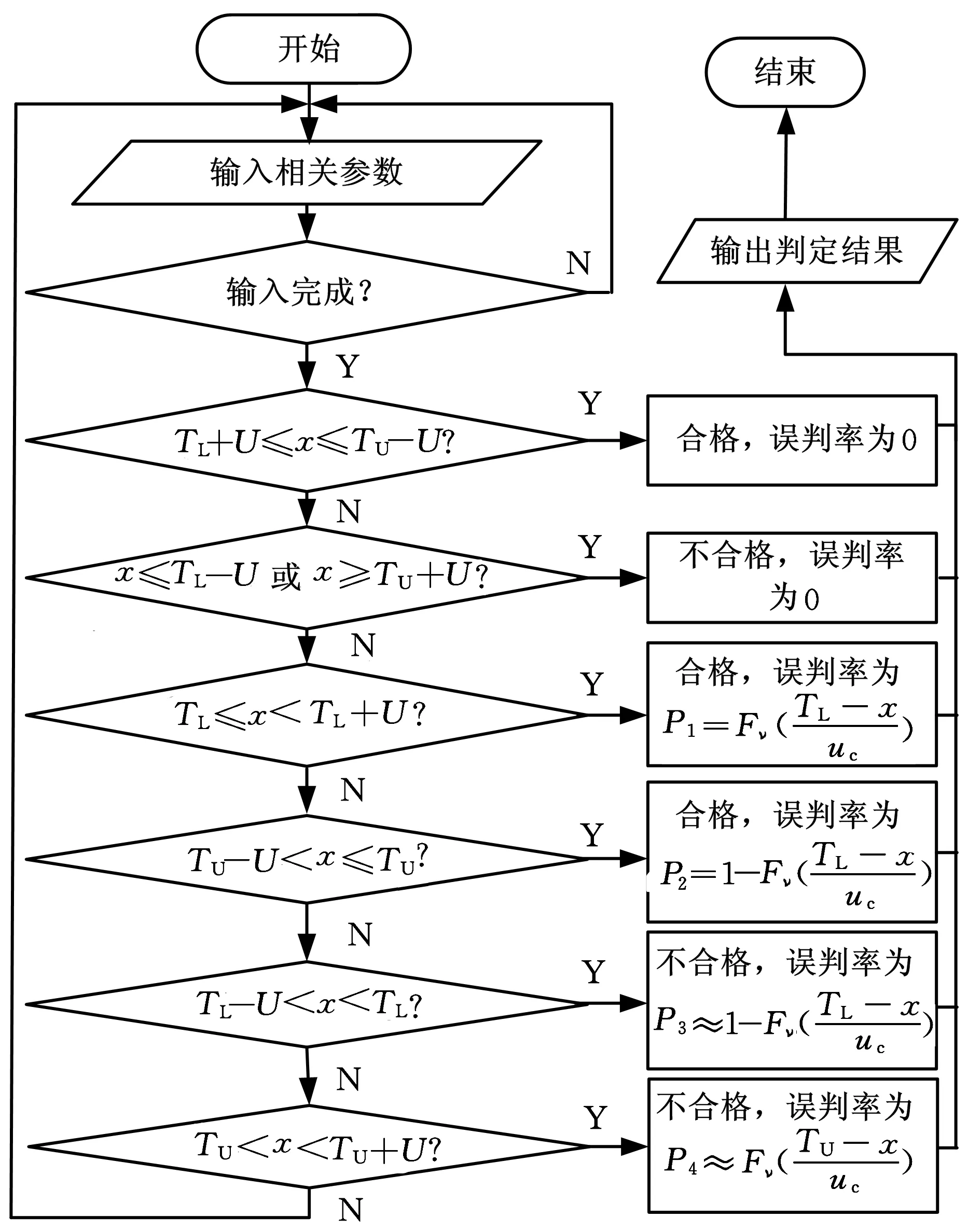
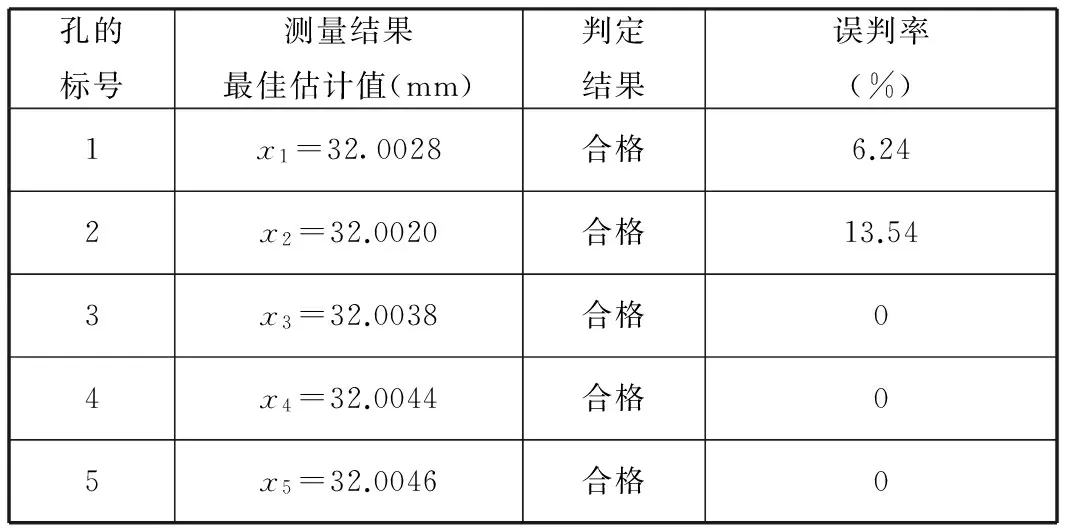
测量不确定度对产品合格判定的影响如图1所示,图中,TL为给定的公差下限,TU为给定的公差上限,U为测量的扩展不确定度。设工件测量结果的最佳估计值为x。根据ISO14253-1的规定,只有当TL+U≤x≤TU-U时,方可判定工件合格;只有当x≤TL-U或x≥TU+U时,方可判定工件不合格;当x位于图1中的灰色区域内时,由供求双方协商确定工件是否合格。一般来说,当测量结果的最佳估计值位于图1中的1、2区域内,即TL≤x 图1 测量不确定度对产品合格判定的影响 2.1批量产品合格判定中误判率的计算 在批量产品的合格判定中,测量结果的最佳估计值x为随机变量,根据中心极限定理,假定x满足正态分布,则x的概率密度函数为 (1) 其中,μ为产品规范的标准值;σ反映批量产品中测量结果最佳估计值的分散性,其计算公式为 (2) 其中,σp反映由加工过程造成的被测量本身的分散性;uc表示测量的合成标准不确定度。设y=x±U为考虑测量不确定度影响后测量结果的表示,则y为x±U内的一个值。对于每一个给定的x值,y的分布密度函数为p(y|x)。根据测量不确定度表示指南(GUM),(y-x)/uc应满足自由度为ν的t分布。其中,ν为合成标准不确定度的自由度。 对于批量产品,将发生“存伪”误判的概率记为PCR(consumer’s risk),将发生“拒真”误判的概率记为PPR(producer’s risk)[5],则 PCR=P(TL≤x≤TU)P(y P(TL≤x≤TU)·P(y>TU)= (3) PPR=P(x P(x>TU)P(TL≤y≤TU)= (4) 记自由度为ν的t分布的分布函数为Fν(x),则式(3)、式(4)可写为 PCR=P1+P2 (5) (6) (7) (8) 由公式推导过程可知,P1对应于发生在下规范限附近(图1中区域1内)的误判率,P2对应于发生在上规范限附近(图1中区域2内)的误判率。 类似地,记 (9) (10) 其中,P3对应于发生在下规范限附近(图1中区域3内)的误判率,P4对应于发生在上规范限附近(图1中区域4内)的误判率。 2.2单个产品合格判定中误判率的计算 在单个产品的合格判定中,测量结果的最佳估计值x为一确定值,此时,可根据x所处的区间进行合格判定。当TL+U≤x≤TU-U时,可直接判定工件合格;当x≤TL-U或x≥TU+U时,可直接判定工件不合格;且根据ISO14253-1,可认为上述判定误判率为0。当x位于图1中的灰色区域内时,所做合格判定可能存在误判。当x位于不同区间时,误判率的情况如图2所示。其中,误判率为图2中灰色部分的面积。 如图2a所示,当x位于图中区域1内时,TL≤x (11) 如图2b所示,当x位于图中区域2内时,TU-U (12) (a)x位于区域1 (b)x位于区域2 (c)x位于区域3 (d)x位于区域4图2 单个产品合格判定中不同区间的误判率 如图2c所示,当x位于图中区域3内时,TL-U (13) 如图2d所示,当x位于图中区域4内时,TU (14) 由上述分析可知,单个产品检验时,首先应判定测量结果的最佳估计值x所在区间,根据其所在区间进行相应的合格判定及误判率计算。为简化合格判定中误判率的计算,编制了基于LabVIEW的合格判定软件,只需输入相关参数,即可获得合格判定结果和可能存在的误判率。软件主界面如图3所示。软件的程序流程如图4所示。 图3 产品合格判定软件主界面 图4 单个产品合格判定软件程序流程图 图5 车载空调压缩机后盖零件 利用三坐标测量机对图5所示的车载空调压缩机后盖零件上标号为1~5的5个孔的直径进行测量,根据测量结果,进行合格判定和误判率计算。 实验前,首先基于ISO 15530-1对坐标测量机孔径测量的不确定度来源进行分析。根据实验和计算结果,孔径测量的不确定度来源和各不确定度分量大小见表1。 表1 不确定度汇总表 考虑到上述各不确定度分量彼此独立,合成标准不确定度为 (15) 合成标准不确定度uc的自由度为 (16) 取ν=63,置信概率P=95%,查t分布表得包含因子k=t0.95(63)=2,则孔径测量的扩展不确定度为 U=kuc=3.6 μm (17) 将测量不确定度评定结果输入合格判定软件作为预知参数。同时依据零件的技术规范,设定5个孔径值的公差下限TL=32.00 mm,公差上限TU=32.03 mm。 在与不确定度评定过程相同的测量条件、测量方法下依次对图5中的5个孔径值进行测量,并分别将测量结果的最佳估计值输入合格判定软件,得到合格判定结果,见表2。 表2 孔径测量合格判定结果 由合格判定结果可知,如果不考虑测量不确定度,零件的5个孔径值全部合格。如果考虑测量不确定度的影响,对于孔3、4、5,判定结果为合格,误判率为零;对于孔1、2,若判定结果为合格,用户将分别承担6.24%和13.54%的误判风险。用户可根据自己所能承受的误判率,决定是否接收零件。误判率计算结果将为供求双方协商确定零件的合格性提供可靠依据。 (1)测量不确定度导致产品合格判定中存在不确定区域,基于不确定度理论的误判率计算可以为供求双方协商不确定区域内产品是否合格提供理论依据。 (2)传统研究在误判率计算时往往以随机误差代替不确定度,然而随机误差仅能反映测量过程中随机的、变化的因素(表1中的测量重复性)对测量结果的影响,不能反映测量过程中系统的、不变的因素(表1中的示值误差、测量再现性)对测量结果的影响,因此,仅以随机误差所确定的误判率是不准确的。 (3)本文以不确定度的分布规律建立误判率计算的数学模型,并初步编制了产品合格判定软件。如果将合格判定软件同测量仪器结合,将有效促进测量不确定度理论在产品检验工作中的推广应用。 [1]李红莉,陈晓怀,王宏涛.坐标测量机测量端面距离的不确定度评定[J].中国机械工程, 2012,23(20):2401-2404. Li Hongli,Chen Xiaohuai,Wang Hongtao.Uncertainty Evaluation of CMM for End Distance Measurement[J].China Mechanical Engineering,2012,23(20):2401-2404. [2]亓四华,费业泰,孙键.基于在线测量的制造质量零废品控制模型的研究[J].中国机械工程,2001,12(2):223-225. Qi Sihua,Fei Yetai,Sun Jian.Research on the Zero-waste Control Model of Manufacturing Quality Based on Online Measurement[J].China Mechanical Engineering,2001,12(2):223-225. [3]彭和平,蒋向前,徐振高,等.新一代产品几何技术规范测量不确定度理论及应用技术[J].中国机械工程,2007,17(24):2535-2539. Peng Heping,Jiang Xiangqian,Xu Zhengao,et al.Theory of Measurement Uncertainty & Its Application in the New Generation Geometrical Product Specifications[J].China Mechanical Engineering,2007,17(24):2535-2539. [4]Macii D,Petri D.An Effective Method to Handle Measurement Uncertainty in Conformance Testing Procedures[C]//2007 IEEE International Workshop on Advanced Methods for Uncertainty Estimation in Measurement.Sardagna,2007:69-73.[5]Macii D,Petri D.Guidelines to Manage Measurement Uncertainty in Conformance Testing Procedures[J].IEEE Transactions on Instrumentation and Measurement,2009,58(1):33-40. [6]Chen J F,Hu Q P.Misjudgment Probability and Quality Control of Manufacture[C]//2011 Third International Conference on Measuring Technology and Mechatronics Automation.Shangshai,2011:564-567. [7]Desimoni E,Brunetti B.Uncertainty of Measurement and Conformity Assessment a Review[J].Analytical and Bioanalytical Chemistry,2011,400(6):1729-1741. [8]Pendrill L R.Using Measurement Uncertainty in Decision-making and Conformity Assessment[J].Metrologia,2014,51(4):S206. [9]Theodorou D,Zannikos F.The Use of Measurement Uncertainty and Precision Data in Conformity Assessment of Automotive Fuel Products[J].Measurement,2014,50:141-151. [10]Phillips S D,Krystek M.Assessment of Conformity,Decision Rules and Risk Analysis[J].Technisches Messen,2014,81(5):237-245. [11]Koshulyan A V,Malaychuk V P.Conformance Assessment for Acceptance with Measurement Uncertainty and Unknown Global Risks[J].Measurement Techniques,2014,56(11):1216-1223. (编辑陈勇) Calculation of Misjudgment Probability in Product Tests Based on Measurement Uncertainty Chen XiaohuaiWang HanbinCheng YinbaoJiang Rui Hefei University of Technology,Hefei,230009 According to ISO14253-1,the principles and methods of conformity assessment were studied based on measurement uncertainty.The effects of measurement uncertainty on conformity assessment in product tests were analyzed,and based on the distribution function of measurement uncertainty,formula of misjudgment probability in batch product quality tests was derived;situations for a single product were then discussed when measurement results were in different sections.Software for conformity assessment was designed based on LabVIEW,from which the conformity assessment results and the misjudgment probability could be acquired simply by inputting related parameters.An actual experiment shows that measurement uncertainty may cause misjudgment in product test. Software for conformity assessment can effectively improve the operability of applying uncertainty theory in product tests,and calculation of misjudgment probability based on measurement uncertainty can provide reliable basis for consumer and producer to reach an agreement on the conformity of products. product test;conformity assessment;measurement uncertainty;misjudgment probability 2014-09-28 国家自然科学基金资助项目(51275148);合肥工业大学青年教师创新项目(JZ2014HGQC0126) TB92;TH124DOI:10.3969/j.issn.1004-132X.2015.14.001 陈晓怀,女,1954年生。合肥工业大学仪器科学与光电工程学院教授、博士研究生导师。主要研究方向为精密测试技术、现代精度理论及应用。获部级科技进步二等奖、三等奖各1项,获省级自然科学二等奖、三等奖各1项。出版专著1部,发表论文60余篇。王汉斌,男,1989年生。合肥工业大学仪器科学与光电工程学院博士研究生。程银宝,男,1984年生。合肥工业大学仪器科学与光电工程学院博士研究生。姜瑞,女,1991年生。合肥工业大学仪器科学与光电工程学院硕士研究生。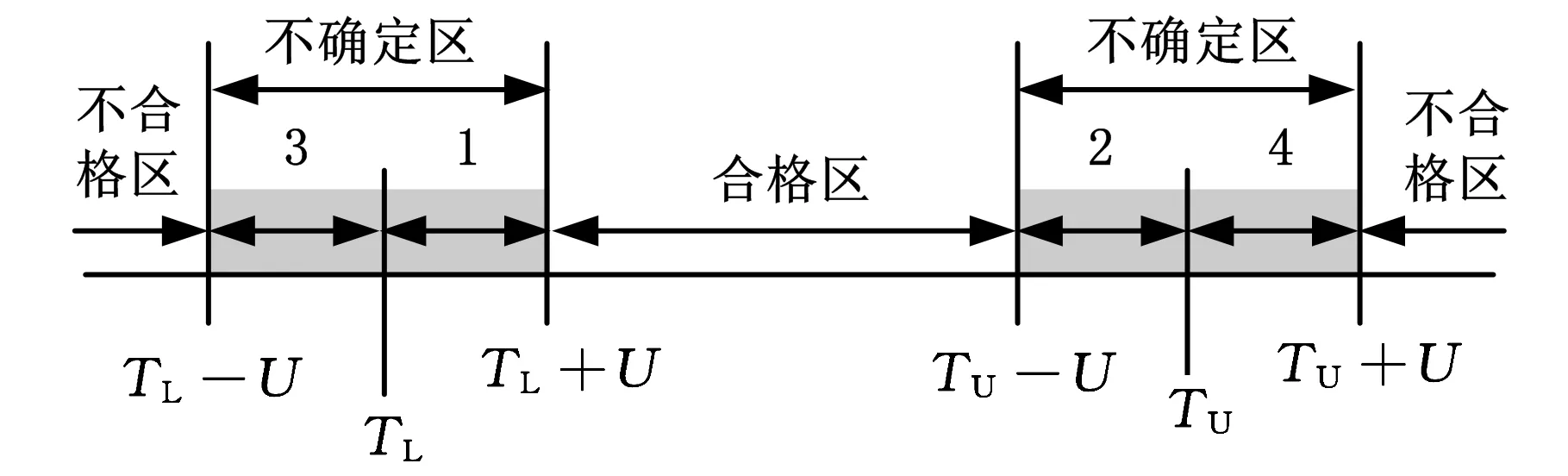
2 产品合格判定中误判率的计算
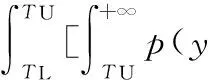
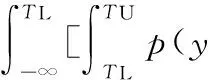
3 基于LabVIEW的合格判定软件

4 实例分析

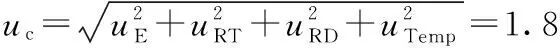
5 结论

