“预学后教”教学模式的探索

周文婉

[摘 要]“预学后教”教学模式是教师依据学生的认知特点，精心设计预学单，通过对预学单的整理、分析掌握学情，再以学定教，实施与学生需求相匹配的针对性教学，培养学生的自学能力和创新精神。

[关键词]平行四边形 面积 预学后教 细心解读 提升能力 掌握学情 以学定教

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2015）23-031

“预学后教”顾名思义就是先自学后教学。预学就是学生在教师的指导下，运用看、思、议、练等形式进行自主的学习；后教是教师针对学生在预学阶段暴露出的问题，进行点拨、引导和矫正。“预学后教”策略下的数学教学，一般可以分为预学、后教、检测三个步骤。下面，我以“平行四边形的面积”教学为例，具体阐述“预学后教”教学模式的操作和实践。

一、预学——掌握学情

预学决不能简单地要求学生回家读一读、看一看课本就了事，而是要设计符合学生年龄特征和知识特点的预学单指导学生学习，并通过预学单的整理、分析，掌握学情。具体做法有以下两点：

1.课前要精心指导

学生掌握预习的方法需要一个过程，我在教学中采用“一尝试，二自学，三生疑”的预习策略。尝试是指教师根据教学内容设计具有挑战性的问题，让学生先行思考、尝试解决问题，在学生探而不明时再安排看书、操作、试验等活动，目的是避免学生把预习等同于自学看书，最后导致自学变成被动的接受或简单的模仿，从而使学生的探究性学习贯穿预习始终。这时的自学，可能是对探得后的进一步确定，也可能是探不得后的充电，使每个学生在自学过程中都能体会到收获的喜悦。生疑是更深层次学习的体现，是学后的反思、质疑与追问。疑问的深度，反映了预习和思考的深度。学生把疑问带到课堂上，使后续学习的动力变得更加强劲。

如教学“平行四边形的面积”时，我设计了这样一份预学单。如下：

“平行四边形的面积”预学单

班级________ 姓名______________

同学们，在三年级下学期我们已经学过长（正）方形的面积计算，下面我们要继续学习有关面积的知识——平行四边形的面积，请你根据要求尝试完成下面各题。

（1）不看书，根据你自己的想法量出下面平行四边形的数据，然后列式计算出这个平行四边形的面积。（设计这道题的目的主要是检验学生已有的经验及知识迁移情况，激发学生探究的兴趣）

（2）你的解答正确吗？请你自学书本第86～88页。

自学要求：

a.书上把平行四边形转化成了什么图形？

b.怎样转化？请你运用剪一剪、画一画、拼一拼等方法进行动手操作。

c.平行四边形和转化后的图形之间有什么联系？

d.求平行四边形的面积除了用“底×高”计算外，还有什么方法？

e.通过自学，你读懂了什么？还有什么不懂的？请把它写下来。

（3）自学后，请你再次列式计算下面这个平行四边形的面积，你的方法和原来一样还是不同？如果不同，现在你认为怎样计算？请把算式写下来。

（再次解决这道题，主要引导学生进行反思、质疑，并追问：为什么不能用底乘临边？）

为了避免学生简单地从书本学习公式，我安排以上自学问题，使学生看一看、剪一剪、想一想，引导学生兴趣盎然地深入探究。

2.预学后要细心解读

了解学生的知识基础，这是有效教学的起点。教师只有重视对学生预学后学情的分析，才能真正做到以学定教。如：学生通过预学学会了什么？还有哪些知识点学生是模糊的？还有哪些方面学生是根本不懂的？学生学习的难点是什么？哪些不同的想法会引发争议……这些都是教师需要考虑和了解的问题。如教学“平行四边形的面积”时，通过预学单的分析，我发现在尝试解答平行四边形的面积计算时，71.4%学生都是采用临边乘高的方法。通过自学，大部分学生已经掌握平行四边形的面积公式。对于转化思想，学生有三种不同层次的体现：第一层次的学生不仅掌握了转化思想，而且能用语言清晰的表达想法；第二层次的学生已有转化思想，但表达模糊；第三层次的学生几乎不会。大部分学生对“怎样转化”“为什么转化”等问题还是比较模糊，而“平行四边形的面积为什么用底乘高而不用临边乘高”的问题则是学生最大的疑问。

二、后教——以学定教

有了预学的基础，课堂的教学起点便相应发生了变化。如何解决学生的疑问、如何拓展和深化学生的学习，成为课堂上教师首当其冲需要考虑的问题。为此，我采用回馈、释疑、整理“三部曲”进行教学。

1.回馈

课堂上，教师设计几个关键性问题，通过学生的回答了解学生的预学情况，这样也可以使学生把自己自学的知识通过交流达到共享的目的。在学生预学“平行四边形的面积”后，我先让学生把学到的知识和大家分享一下，因为每个学生在自学过程中多多少少都有点收获。学生交流的兴致很高，有的说平行四边形的面积可以用“底×高”来计算，有的说可以把平行四边形转化成长方形求出面积。然后我抓住这个问题让学生演示平行四边形转化成长方形的过程，这样既给优等生一个展示的平台，又通过生教生的形式，达到共同发展的目的。接着，让学生提出心中的疑问。因课前的预习给了学生足够的时间和空间思考，所以课堂上学生提出了许多有研究价值的问题，如“是不是所有不同形状的平行四边形都能转化成长方形”“为什么要把平行四边形转化成长方形”等。

2.释疑

教学中，教师对学生提出的有价值的问题，要引导学生根据这些问题展开新一轮的探究，从而有利于教学的拓展和深化。如教学“平行四边形的面积”这一课，我先引导学生对“除了沿着从顶点出发的这两条高剪外，我们还能沿着其他的高剪吗？剪下来的图形还能拼成长方形吗”这一问题展开探究，学生在剪拼中自己就解决了这个问题，然后让学生把剪拼的图形贴在黑板上。通过观察，学生轻而易举地解决了“平行四边形能剪拼成正方形吗”“怎样的平行四边形能拼成正方形？是不是所有的平行四边形都能转化成长方形”“平行四边形和长方形之间有什么联系”这几个问题。于是，我借助课件引导学生进行更深入的探究：“为什么所有的平行四边形通过剪拼都能刚好拼成长方形？用‘底乘临边这种方法求平行四边形的面积为什么不对呢？”……有了“预学”作基础，教师可以从容地组织学生进行剪一剪、比一比等操作活动，让学生在丰富的实践体验中加深对知识的理解，揭示知识背后的奥秘。

3.整理

由于学生的年龄、心理、知识经验以及学习水平的不同，所以学生理解问题的水平也各不相同。通过预学得到的知识往往是零碎的、模糊的、不系统的，这时就需要教师引导学生加以提炼。如教学“平行四边形的面积”一课时，在学生得出平行四边形的面积公式后，我趁机提出问题“为什么把平行四边形转化成长方形，转化成别的图形行吗”，从而引发学生更深层次的思考，让学生透过现象发现问题的实质。这样教学不仅让学生对知识掌握得更牢固，而且使知识更具有迁移作用，为后面学习三角形、梯形的面积公式做好充分的准备。

三、检测——提升能力

检测的目的是化知识为能力。检测的内容要根据不同学生的认知水平，设计多层次的习题，主要通过变式、求异、拓展等方式，帮助学生加深对知识的理解。这对于帮助学生巩固和检验新知，培养学生分析问题和解决问题的能力，尤其是培养学生思维的广阔性和深刻性及创造能力都有重要意义。如教学“平行四边形的面积”一课时，主要设计以下三个层次的练习。

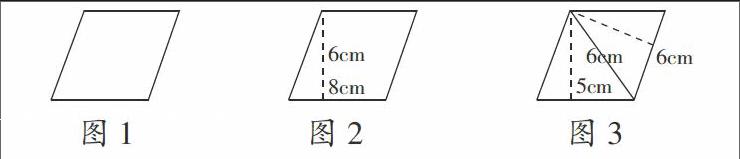
第一层次：基础练习。

出示图1后，要求学生说说求平行四边形的面积需要什么条件，再出示图2、图3，让学生计算平行四边形的面积。

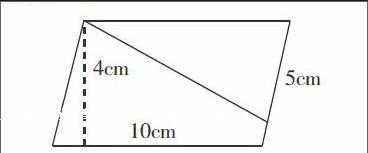
第二层次：拓展练习。

先求出平行四边形的面积，再求出5cm底边上对应的高。

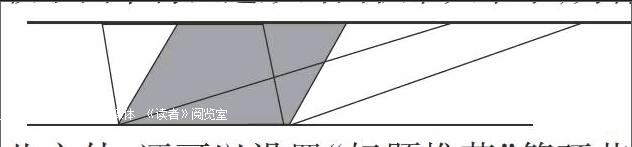
第三层次：深化练习。

比较下面平行四边形的面积谁大谁小，为什么？

除此之外，还可以设置“好题推荐”等环节，让学生把收集到的好题以“小老师”的身份考考大家，然后讲解自己的思路。这样不仅丰富了教学资源，让学生体验到了学习的成功，而且培养了学生的表达能力，使不同的学生得到不同的发展。

总之，“预学后教”指导下的课堂教学，需要教师依据学生的认知特点，精心设计预学单，通过对预学单的整理、分析掌握学情，再在此基础上合理地组织导学过程，真正实现以学定教，培养学生自主学习的能力。

[ 参 考 文 献 ]

[1] 顾泠沅.教学改革的行动与诠释[M].北京：人民教育出版社，2003.

[2] 张奠宙.数学教育学导论[M].北京：高等教育出版社，2003.

（责编 杜 华）