基于Fluent的气力输送弯管磨损分析

徐寒冬，田世伟，杨道龙，李林宁

（1.中国矿业大学 机电工程学院，徐州 221116；2.中国矿业大学 孙越崎学院，徐州 221116）

0 引言

气力输送是利用压缩空气在管道中进行长距离输送物料的一种技术，其与一般输送方式相比具有环境适应性强、设备布置灵活、维修保养方便以及易于实现自动化等优点，在化工、能源、农业、矿业等方面得到广泛的应用，并越来越受到人们的关注[1,2]。将气力输送系统用于煤矿井下采空区矸石充填，不仅能减少矸石的运输及处理费用，同时也能有效避免采空区塌陷、矸石山污染环境等问题，符合煤矿绿色开采要求[3]。然而将气力输送用于煤矿井下矸石充填面临着能耗高和管道磨损严重的问题，该问题在管道转弯处表现尤为严重[4,5]，因此本文将针对矸石在气力输送过程中对弯管的磨损情况进行分析。

气力输送过程中，影响管道磨损情况的因素很多，王公忠等人[6]论述了物料性质、管路铺设以及管道直径等因素对磨损情况的影响，孙运森[7]论述了充填物料、充填倍线以及管压等因素对磨损情况的影响，本文将从物料颗粒粒度、气流速度以及弯管弯曲半径与管道内径比值（弯径比）三方面进行研究，分析其对弯管磨损的影响。

1 仿真模拟

本文采用颗粒轨道模型，其适用于稀相气力输送求解,考虑颗粒与管壁的碰撞，可以研究颗粒对管道的磨损。该模型将流体相作为连续介质，将颗粒相看成离散相，流体相和颗粒相之间可以交换质量、动量和能量等。对于本文研究的矸石颗粒气力输送，空气作为流体相，而矸石颗粒作为颗粒相。

1.1 数学模型

1）连续性方程

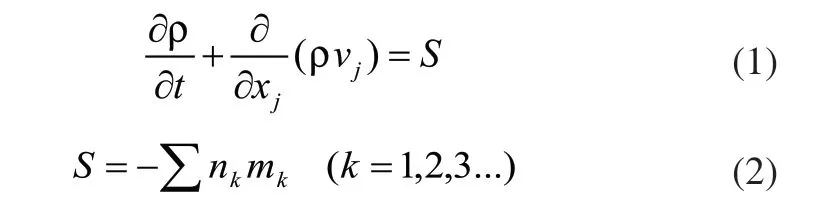
式中，ρ为气相密度，kg/m3； xj为j方向坐标；vj为气相沿xj坐标方向速度分量，m/s；S为气固两相混合物中单位体积颗粒相的体积分数； nk为第k种颗粒相的数密度；mk为第k种颗粒相的单颗粒质量。

2）动量守恒方程

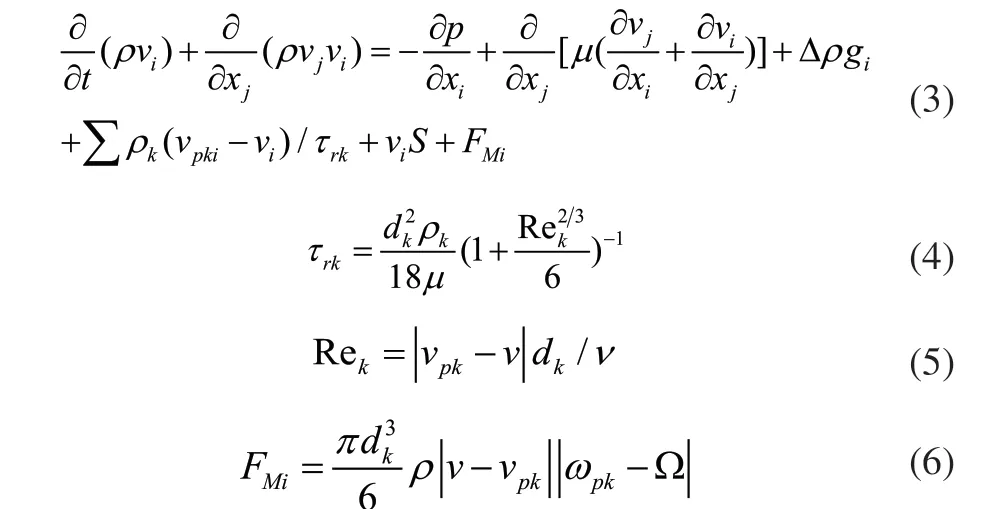
式中，μ为空气动力粘度，Pa.s；ρk为气固两相混合物中第k种颗粒相的密度，kg/m3；vpki为第k种颗粒相沿xj坐标方向速度分量，m/s；τrk为第k种颗粒相扩散弛豫时间，s；dk为第k种颗粒相的粒度，m；Rek为第k种颗粒相相对运动雷诺数；ν为气相运动粘度，m2/s； FMi为颗粒受到的Magnus力，N；ρ为气相时均密度，kg/m3；ωpk为第k种颗粒相颗粒旋转角速度，rad/s；Ω为气相涡量的一半。

3）能量守恒方程

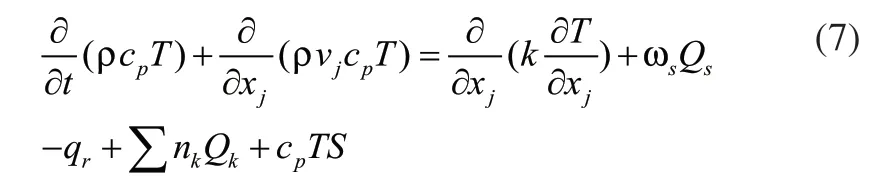
式中，cp为比热，J/(kg⋅K)；T为气体相温度，℃； k为热导率，W/(m⋅s)；ωsQs为气体相反应在单位体积中释放的热量，在这里ωsQs=0；qr为气体相的辐射传热，qr=0；Qk为颗粒与气体间的对流传热，Qk=0；cpTS为气体相相变产生的源项。

4）矸石颗粒运动方程

式中，vp为颗粒沿x方向的速度分量，m/s； mp为颗粒的质量，kg； Fd为颗粒所受到的流体阻力，N；Fg为颗粒所受到的重力，N； Fx为颗粒所受到的其他外力，N；其中流体阻力公式为：

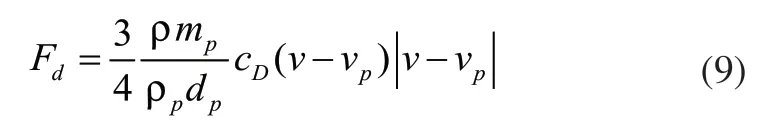
式中，Fd为矸石颗粒受到的流体阻力，N；ρp为矸石颗粒密度，kg/m3； dp为矸石颗粒的粒度，m； cD为阻力系数； v为气流速度，m/s； vp为颗粒速度，m/s。

5）管道磨损方程[8]

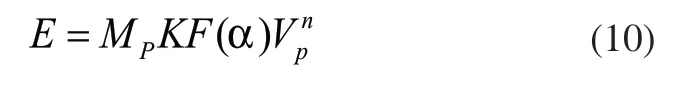
式中，E为管壁磨损量； Mp为固体颗粒的质量， kg； K为与颗粒性质有关的常数，K=1.8×10-9；α为颗粒对壁面冲击角； ()Fα为冲击角函数，取 ()Fα=1；Vp为颗粒相对于管壁的速度；n为速度指数．

1.2 数值模拟模型

Fluent提供了两种求解颗粒轨迹的方法，一种是不考虑颗粒对于气相的影响，称为非耦合求解；另一种则是考虑颗粒对于气相的影响，称为耦合求解。气力输送过程存在气相与颗粒相的强烈相互作用，因此本文采用耦合求解方法。

利用Gambit软件构建圆柱形管道模型，采用Hex单元类型和Cooper划分方法对管道进行网格划分。为此利用虚拟几何结构分割直管端面，把圆端面分割为5个逻辑四边形，然后对5个逻辑四边形进行网格划分，最后利用Cooper方法对整个体积进行网格划分。弯管模型和网格划分如图1所示，由弯头和两段直管（合称弯管）组成，弯管内径和弯曲半径分别为d和R，入口和出口端直管的长度分别为Hr和Hc，管道弯曲角度为90°，管道内径设为70mm。另外一个表征弯管几何结构的重要参数是弯曲半径R与管道内径d的比值δ。仿真求解时，管道的进口和出口边界条件分别定义为速度入口和压力出口，颗粒相定义为球形矸石颗粒，矸石密度设置为2800kg/m3。

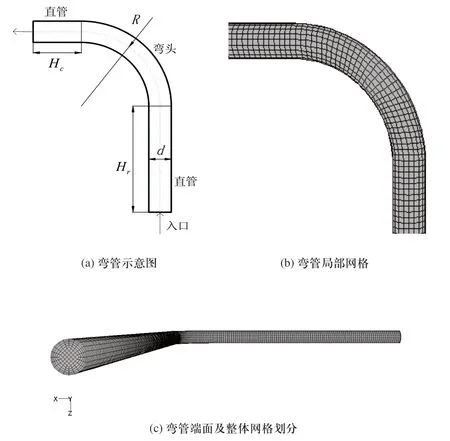
图1 弯管模型

2 仿真结果及分析

2.1 颗粒粒度和气流速度对弯管磨损的影响

用于充填的矸石粒径一般在0~50mm之间，且粒径越小，充填效果就越好[9]，因此本文将分别对5mm、10mm、15mm粒径的矸石颗粒进行仿真模拟。图2和图3分别是气流速度为40m/s和70m/s时，输送不同粒度矸石颗粒造成弯管磨损率等值图。图中箭头表示弯管中气体-颗粒流的方向，只在图a中标出，其他图类似。为表示弯管中磨损发生的位置，分别画出沿管道轴向六等分截面（如图中0deg-90deg所示）和z坐标方向z=0.02、0.01、0、-0.01、-0.02截面，形成如图所示的网格线。

从图2和图3可以看出，随着粒度的增加，弯管最大磨损率逐渐减小。从总体来看，最大磨损率沿管道轴向的位置出现在20°～35°的范围内，示意在图4中阴影部分，这和Derrick O.Njobuenwu等[10]得到的结论是一致的。 在z轴方向上，对于两种气流速度，最大磨损率都出现在0～-0.02的范围内，即管道的中间偏下位置。从磨损率大小分布来看，磨损率围绕最大磨损位置呈现片状分布，从片状由内到外，磨损率逐渐变小，这主要是由于管道的二次圆柱曲面造成颗粒在截面中间位置分布较多造成的。值得注意的是，当气流速度增大后，最大磨损率增大非常明显，速度从40m/s增大到70m/s，最大磨损率增大了3个数量级，而且还会形成另一个磨损率较大的点，检查颗粒轨迹发现这是因为颗粒与管壁第一次碰撞后，反弹回入口直管内，重新加速后又与管壁发生第二次碰撞，于是增大了最大磨损率，甚至出现两个磨损值较大位置，所以对于矸石颗粒气力输送中的气流流速要在满足要求的前提下，尽可能减小气流流速。

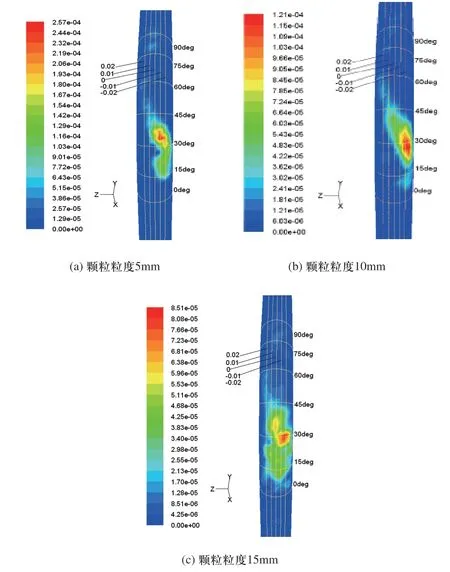
图2 气流速度40m/s时弯管磨损率等值图

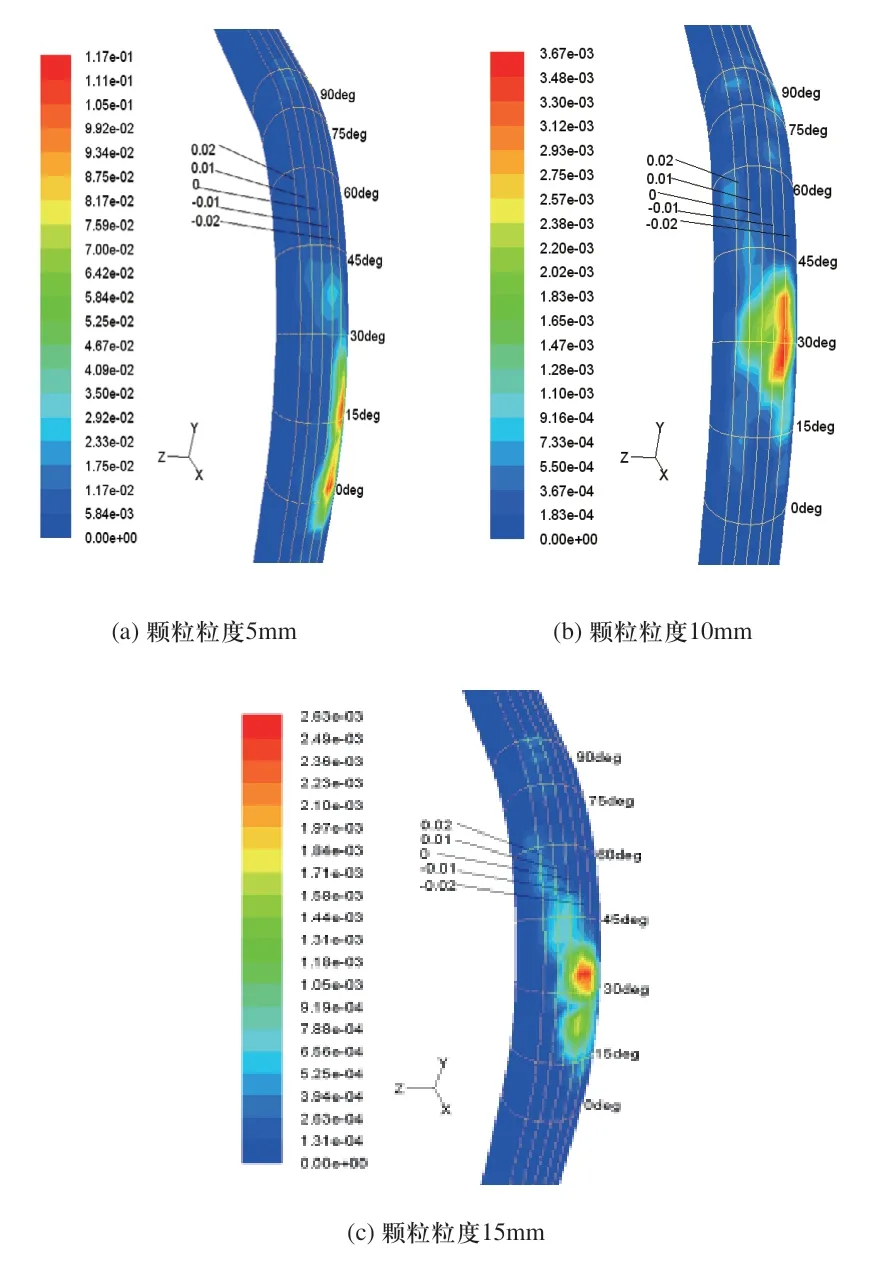
图3 气流速度70m/s时弯管磨损率等值图

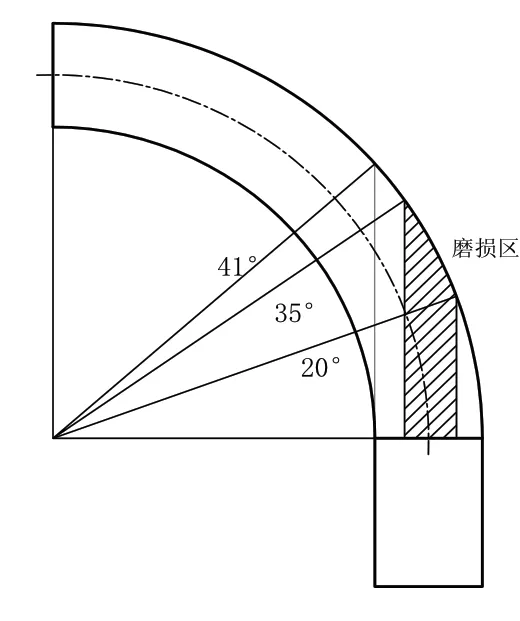
图4 弯管磨损位置示意图

2.2 弯径比对弯管磨损的影响

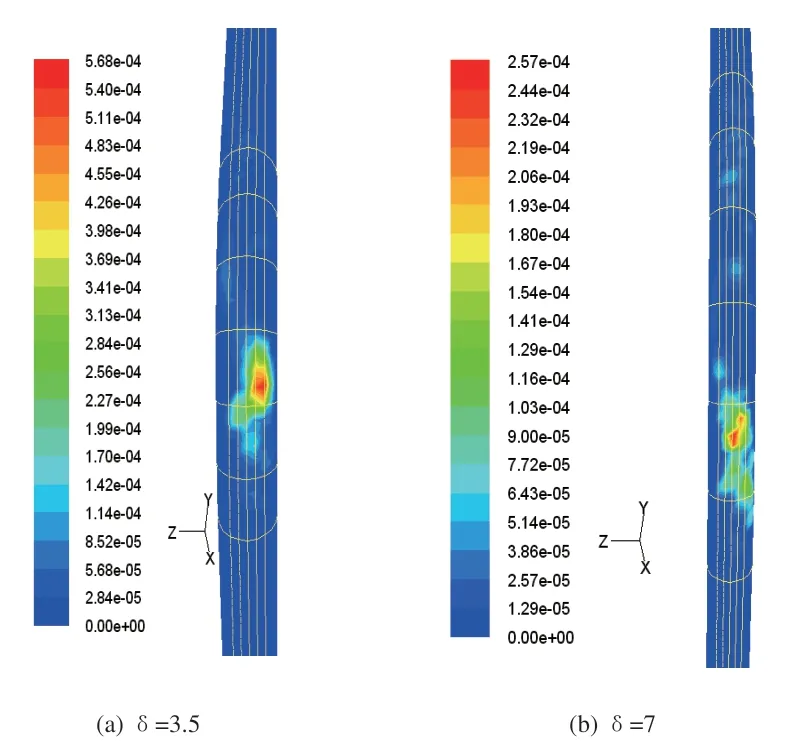
对四种弯径比的弯管进行了模拟，其弯径比分别为3.5、7、10.5和14，入口端和出口端直管长度分别为2m和3m，颗粒粒度为10mm，气流速度40m/s，弯管磨损率等值图如图5所示。随着弯径比的增大最大磨损率逐渐下降，下降的倍数约为弯曲半径的增大倍数，这可以结合图6中阴影部分的面积来说明。用管道内径d和弯径比δ来示弧长为：

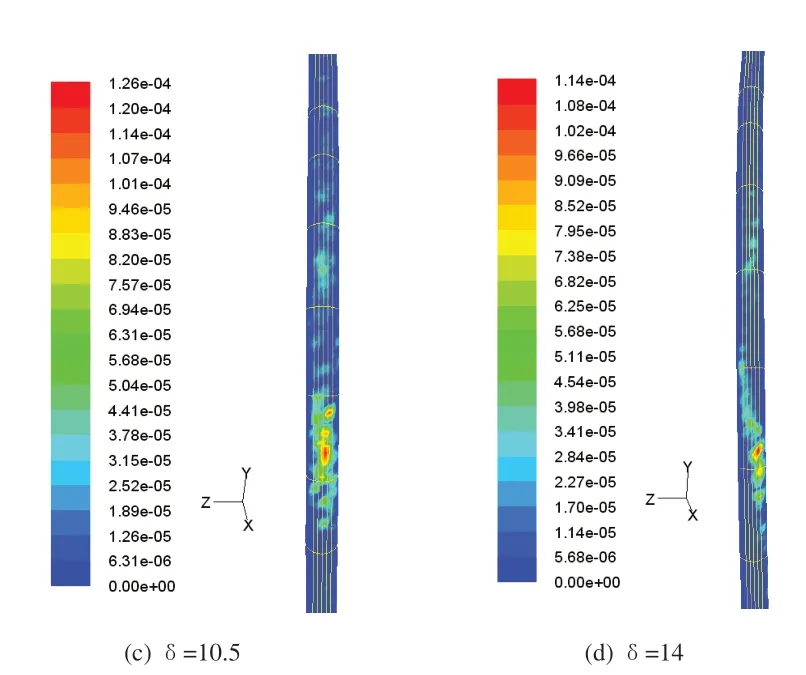
图5 四种不同弯径比δ的弯管磨损率等值图

弧长l随着δ的增大而增大，这意味着从直管中冲撞过来的颗粒将分散在更宽的范围内，所以会带来最大磨损率的下降。从最大磨损位置来看，随着弯径比的增加，最大磨损位置对应的角度在减小，这和图6中虚线对应的位置是一致的，即最大磨损率位置位于入口端直管纵向对称面内。

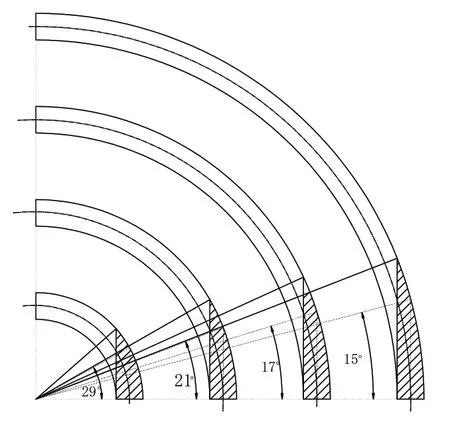
图6 四种不同弯径比δ的弯管高磨损区示意图

3 结论

通过Fluent软件对弯管磨损进行模拟仿真，结果表明在其他条件相同的情况下，增大颗粒粒度和弯径比δ都可以减小弯管最大磨损率，而增大气流速度会增大弯管最大磨损率。因此在条件允许的前提下，可以考虑适当增大颗粒粒度以及采用大弯径比弯管来减少磨损，对于气力输送中的气流流速要在满足要求的前提下将其尽可能减小。

弯管最大磨损率位置与弯管几何结构密切相关，位于入口端直管纵向对称面与弯管的交线附近，所以可对这个区域进行加厚或热处理，增大管道局部耐磨能力，也可以通过改变弯管结构将此区域设计成方便更换的部件来应对磨损问题。

[1] 楼建勇,林江.气力输送系统的研究现状及发展趋势[J].轻工机械,2008,26(3)：4-7.

[2] 齐学武.浅析气力输送系统应用[J].有色矿冶,2014,30(3)：54-56.

[3] 张吉雄,缪协兴,郭广礼.矸石直接充填采煤技术发展现状[J].采矿与安全工程学报,2009,26(4)：395-401.

[4] 李勇,朱秀苹.气力输送中弯管磨损的影响因素及解决办法[J].起重运输机械,2008,9：77-80.

[5] 王中营,张海红,武文斌等. 物料颗粒在弯管内的摩擦磨损与运动分析[J].粮食与饲料工业,2014,12：15-17.

[6] 王公忠,吴金刚. 泵送矸石充填管道磨损与堵塞成因分析[J].中州煤炭,2013,4：57-59.

[7] 孙运森.管道磨损因素与防治技术分析[J].煤炭技术,2014,33(8)：313-314.

[8] Tilly G P. Erosion by impact of solid particles[A].Treatise on Material Science and Technology[C].New York：Academic Press,1979．

[9] 题正义,秦洪岩,李树兴.矸石充填的压实特性试验分析[J].水资源与水工程学报,2012,23(4)：129-131.

[10] Derrick O.Njobuenwu,Michael Fairweather.Modelling of pipe bend erosion by dilute particle suspensions[J].Computers and Chemical Engineering 42(2012)235-247.