基于随机场理论的结构不确定性表征与量化
王春水,李大磊,张二亮
(郑州大学 机械工程学院,郑州 450001)
0 引言
实际结构材料属性的复杂性以及机械加工过程中的各种随机误差等因素会造成结构参数的不确定性,使得材料相同、按相同方法加工出的名义尺寸一致的一组结构件之间存在不确定性,其动力学特性相似但不尽形同,这就需要建立一个有效的模型来表征结构的不确定性。樊征兵等[1]采用了随机因子法、区间因子法和摄动法对弹性模量、密度和截面积参数存在不确定的桁架结构进行模态分析,其中摄动方法适用参数较小的变动,对于一般情况蒙特卡罗模拟有很好的适用性,但其计算量很大,而响应面模型可很好地提高效率简化计算,Fang S E等[2]运用二次多项式响应面模型和蒙特卡罗模拟的方法来量化随机模型弹性模量、密度、惯性矩等参数的不确定性。而实际上引起结构不确定性的参数有很多,这些参数在结构空间上随机分布,为更好地反映实际情况,把结构参数看成是随空间位置而变化的随机变量的随机场理论被引入工程结构数据分析以描述材料参数的空间相关性。白长青等[3]把转轴的弹性模量、剪切模量、密度等参数表示为一维随机场函数,研究了不确定性转子系统的随机有限元建模及响应分析;Feng X等[4]运用均匀随机场表征各有限元单元弹性模量的不确定性,研究了简支梁和层流板的动力学特性。
目前关于结构不确定性的表征及参数修正主要是针对某些结构或材料参数,如弹性模量、惯性矩、厚度等的参数模型进行的,对其均值及方差做不确定性分析,其模型本身的复杂度不高,虽然可以采用各种有效的方法进行随机有限元分析,但并不能很精确地反映实际结构。
针对结构弹性模量的不确定性,提出一种基于随机场理论的超参数模型来表征一组结构属性参数的不确定性,并用参数估计的方法对模型参数进行量化。为表征和量化这种不确定性,首先提出一个基于高斯核函数的随机场模型来表征参数的不确定性,用K-L展开来模拟该随机场超参数模型,对模型进行频率分析,用多元核密度估计估计出输出响应的概率分布密度函数,把试验和模拟结果进行对比运用最大似然估计来量化模型的参数。最后通过对一个算例进行数值试验验证了提出方法的有效性;同时考虑了结构尺寸误差对参数量化的影响。
1 不确定性的随机场表征
机械加工、热处理及材料自身的不确定性等误差都会导致结构的不确定性,这些误差一般都很小且相互独立,根据中心极限定理相互独立的大量微小随机变量,其分布服从高斯分布,高斯分布假设便于计算使问题可解。因此可采用高斯随机场模型来描述一组结构弹性模量的不确定性。
1.1 高斯随机场模型
高斯随机场有以下两个特点[5]:1)其数学期望和方差为一个与位置坐标无关的常数,即为一随机数,xi表示空间一点;2)其自协方差函数只与随机场上两点相对位置距离有关而与两点的绝对位置坐标无关,即为两点之间的相对距离,为自相关函数,相关距离L是其重要的参数,表示在相关距离内的两点的参数具有明显的关联性。建立随机场的关键是构建协方差矩阵。
在有限元框架下,要将连续随机场离散为随机变量向量。对于高斯随机场,常用的离散方法有:谱表示法、Karhunen -Loeve展开法等。这里选用K-L展开法。
1.2 Karhunen-Loeve展开
K-L展开的实质是将随机场分解为一系列不相关的随机变量和确定系数(特征函数、特征值)。其具有以下优越性:对于任意类型随机场都是均方收敛的;相较于其他方法,展开相同有限项时具有最小的均方误差[6]。随机场(,)EXω的K-L展开式为[7]:
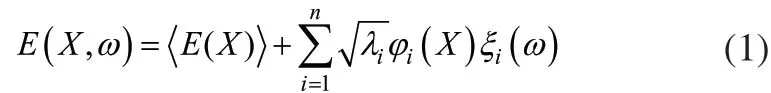
式中:X= (x,y)为空间点坐标;为随机场的期望: ξi(X)为零均值互不相关的高斯随机序列;ω为随机事件; λi和 φi(X)分别为随机场协方差矩阵CE(x,y)的特征值和特征函数。
可见,随机场K-L展开的关键是获得协方差矩阵的特征值和特征函数。所研究的随机场的协方差矩阵是定义在规则几何空间域上的,其表达式易知,可较容易地得到其特征值和特征向量,从而可以较容易地实现随机场的K-L展开。
2 结构不确定性量化
对于所提出的高斯随机场模型,表征结构不确定性的参数是未知的,需要对其进行量化。将试验和模拟的输出响应的分布特征进行对比,对其结果做最大似然估计来量化模型的参数。最大似然估计是一种在给定统计特性下估计参数的方法,而模型的输出响应的分布特征是未知的,这就需要对输出响应的概率分布做非参数估计,核密度估计是常用的一种非参数估计方法。
2.1 核密度估计
设S1,S2,...,Sn是独立同分布随机变量,其分布密度函数的多元核密度估计可表示为[8]:
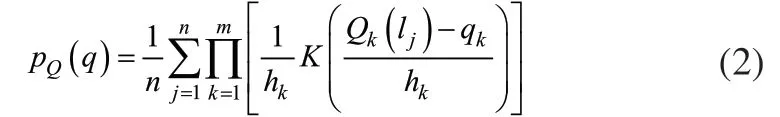
2.2 最大似然估计
对结构的输出响应做最大似然估计,估计出满足概率分布密度的参数,把可能性最大的那个参数作为真实的估计量。对数似然函数更易处理,故对于如式(2)所示的核密度估计函数,其对数似然函数可以表示为:

其中,Qexp为试验输出响应;Qmod为模拟输出响应;num为试验点数;选择多元高斯分布的核函数假设[8],取窗宽为,核函数为
3 算例验证
用MATLAB软件进行数值试验,试验模型为悬臂梁,其参数为:长1m,横截面积0.06m×0.06m,质量密度为7800Kg/m3,有限元建模时将梁划分为50个单元,如图1所示。
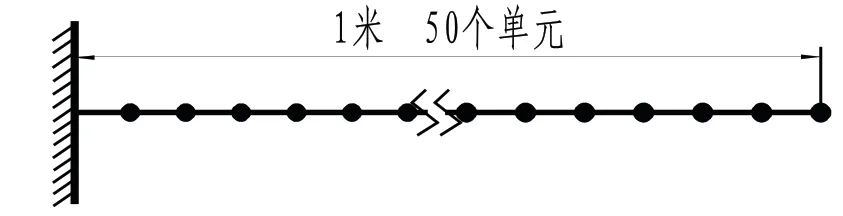
图1 悬臂梁模型
每个单元的弹性模量可以通过式(1)按梁的有限元单元展开得到。其中n=50,均值,协方差函数取为。则弹性模量E的不确定性随机场就由标准差和相关距离L进行表征,超参数也即是试验设计中的输入参数,通过数值试验进行量化。输出响应为每根梁的前四阶固有频率,这些梁的输出响应组成固有频率矩阵S。取输入参数为的500根梁的固有频率矩阵Sexp为试验数据,取输入参数为σ∈{1.0,1.2,1.4,…,3},L∈{10,20,30,…,100}的10000根梁的固有频率矩阵Smod为模拟数据,对Sexp和Smod进行核密度估计和最大似然估计,验证超参数的可辨识性和随机场模型的有效性。
3.1 实验数据分析
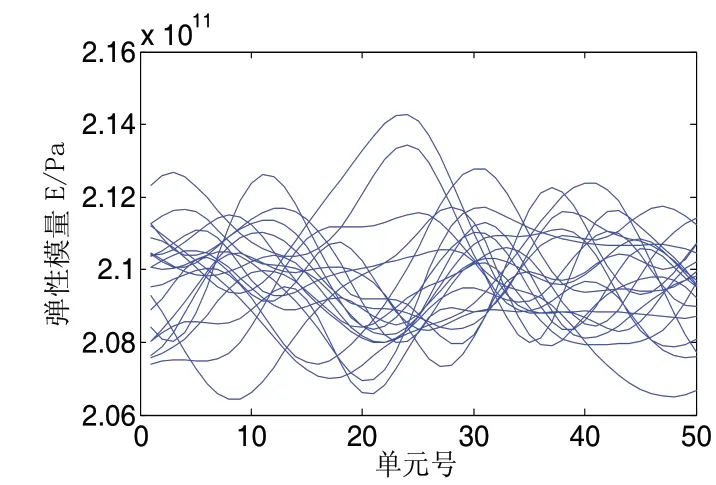
图2 梁单元弹性模量的随机分布
3.2 一维核密度估计
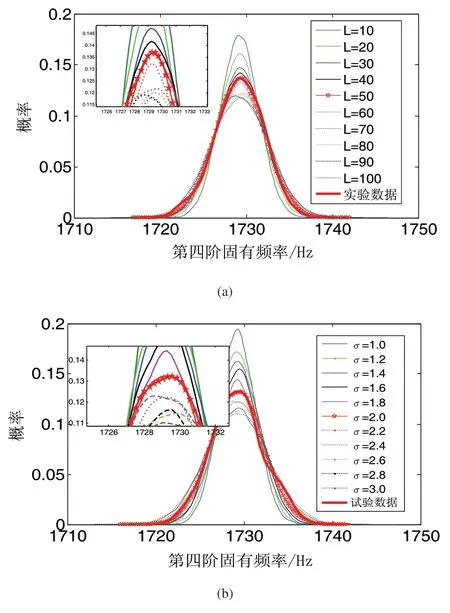
图3 一维核密度估计
可见实验数据的概率密度分布规律与L0=50和σ=2的实验数据的概率密度分布规律最为接近。
3.3 多维核密度估计及最大似然估计
为了更加充分地说明问题,要对Sexp和Smod进行四维核密度估计并在此基础上做关于参数的最大似然估计。由于一些点处的概率密度函数值很小,为避免连乘时似然函数为0,故先对概率密度函数值取对数再连加,同时为了使结果凸显便于观察,对对数似然函数值做指数处理。最终可得到似然函数的三维图如图4所示。

图4 似然函数数值
4 结论
提出的基于随机场理论的超参数模型能够表征结构的不确定性,反映结构参数的不确定性与空间关联性,可以描述实际结构参数的随机变化特性。算例表明,模型超参数可以通过结构的输出响应进行量化,得到结构超参数的标准差和自相关距离,具有一定的应用性。提出的方法也适用于其他参数,也可对其他材料参数或结构参数建立随机场超参数模型并进行量化。
[1] 樊征兵,何欢,陈国平.不确定结构的模态和动响应分析[A].第十届全国振动理论及应用学术会议论文集(2011)上册[C].2011.
[2] FANG S E, REN W X,PERERA R. A stochastic model updating method for parameter variability quantification based on response surface models and Monte Carlo simulation[J].Mechanical Systems and Signal Processing,2012(33):83-96.
[3] 白长青,张红艳.不确定性转子系统的随机有限元建模及响应分析[J].动力学与控制学报,2012,10(3):283-288.
[4] FENG X, LU Z X, YANG Z Y, et al. Analysis on the variances of material and structural properties based on random field theory[J]. Probabilistic Engineering Mechanics.2011(26):222-230.
[5] 张继周,缪林昌.基于随机场理论的地基概率沉降分析[J].岩土工程学报,2010,32(7):1059-1064.
[6] 李少龙,杨金忠,张家发.KL展开在渗流场随机分析中的初步应用[J].长江科学院院报,2009,26(10):39-43.
[7] BETZ W, PAPAIOANNOU I, STRAUD D. Numerical methods for the discretization of random fields by means of the Karhunen-Loève expansion[J].Computer Methods Applied Mechanics and Engineering.2014(271):109-129.
[8] SOIZE C. A computational inverse method for identification of non-Gaussian random fields using the Bayesian approach in very high dimension[J].Computer Methods Applied Mechanics and Engineering,2011(07).

