基于小波包和GA-LM-BP神经网络的汽轮机故障诊断

焦圣喜，迟 警，李婉珍

（东北电力大学 自动化工程学院，吉林 132012）

0 引言

旋转机械是电力、石化、冶金、等行业广泛使用的关键设备[1]。汽轮机转子是火电厂中的重要旋转设备，如果600MW的汽轮机转子发生振动故障使转子停转48小时，其经济损失将达到上千万元[2]。采取合理的措施，对汽轮机转子故障进行预防就显得格外重要。汽轮机转子振动信号能体现出大量转子运行的状态信息，对转子振动信号进行研究能够了解产生故障的机理，并可提取出故障特征，从而达到对机组振动故障诊断的目的。

1 振动信号的预处理

本文采用南京中大趋势测控设备有限公司生产的CUT-2转子振动试验台对相关故障信号进行模拟，应用快速傅立叶变换(FFT)对模拟信号进行频谱分析。传统的硬阈值小波消噪方法对小波系数的压缩是不连续的， Shannon熵的最优小波包基降噪法可以充分克服硬阈值小波降噪中不连续性的缺点。

信号x(t)的小波包分解是把x(t)映射到小波包基上，得到一组系数d1，并用这一组系数表示信号x(t)的特征。运用最优小波包基对初始信号进行分解，分解结果可使初始信号的信息损失达到最小。定义信号的代价函数如下：

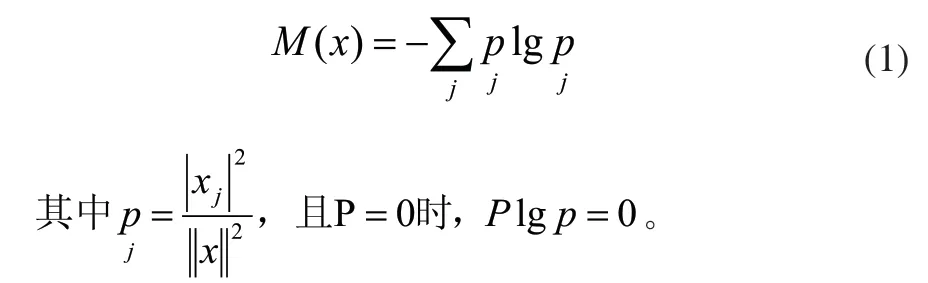
记x={xj}为空间V的一个向量,其一个正交基设为B，x在B下的系数为Bx。在中，如果M(BX)最小，那么B是最优基[3]。采用信号分析中白噪声的Blocks信号作为原始信号，利用小波包变换,分别对Donoh硬阈值消噪算法与本文提出的降噪方法进行对比。信号的最优小波包基如图1所示。

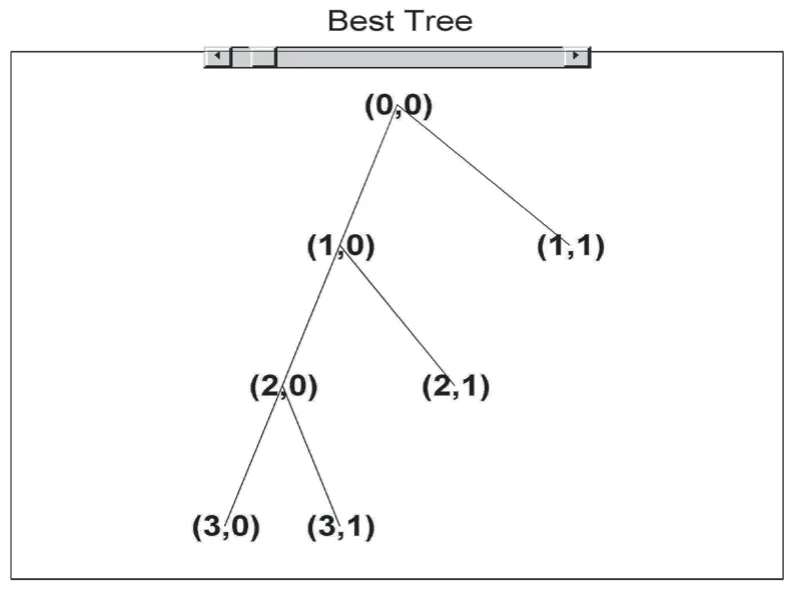
图1 含噪blocks信号的最优小波包基

去噪结果如图2所示，从上至下依次为初始信号、传统硬阈值降噪信号、最优小波包基降噪信号。由图中的平滑度参数值可见，最优小波包基分解结合特定频段阈值选取算法比传统Donoho硬阈值降噪算法具有显著优势。

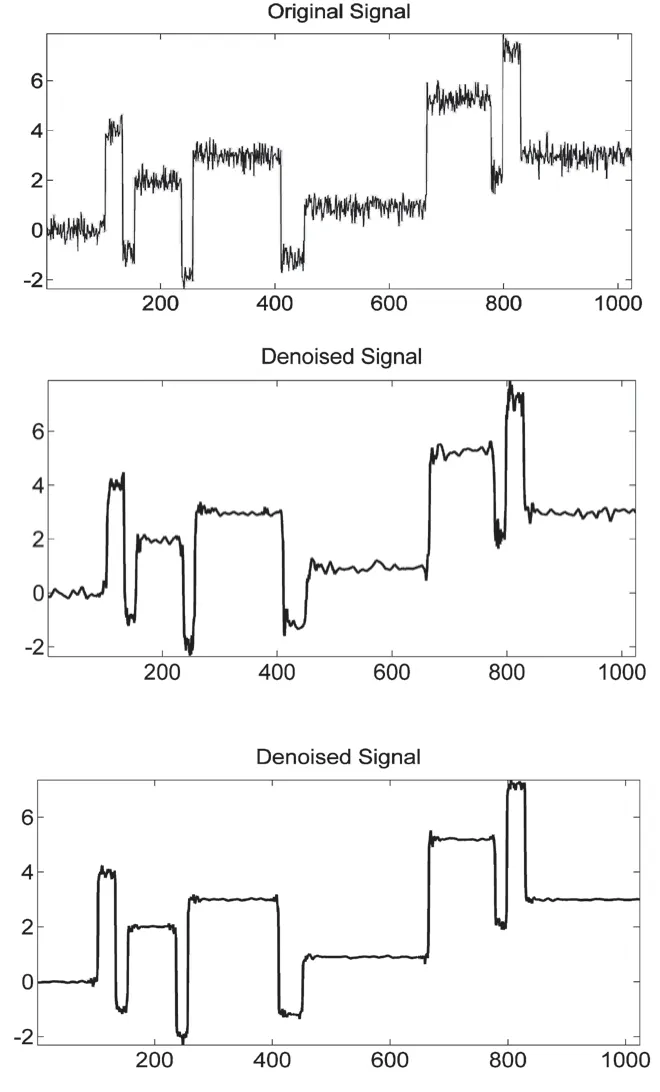
图2 Blocks信号降噪对比图

采用上述降噪方法对实验得到的一组模拟汽轮机振动信号进行降噪预处理，如图3所示，依次为转子不平衡、不对中、油膜振荡、蒸汽涡动、轴承座松动、转子径向磨碰和正常态七种信号去噪后波形图。

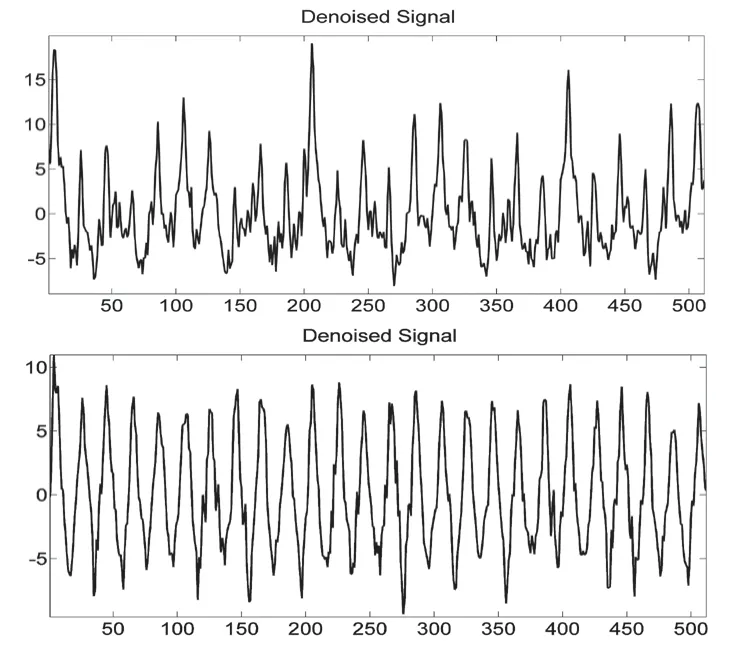
图3 振动信号去噪后波形

2 小波包分析提取故障征兆表

2.1 小波函数简介

传统的快速傅立叶变换只能对平稳信号进行频域（或时域）有效分析，不能兼顾信号在频域和时域的整体和局部信息。小波包分解能够将非平稳信号分解成由小波平移或伸缩构成的基函数族，对待处理信号在不同尺度上进行分解与重构，可以得到原信号在各个频段上的分布信息。

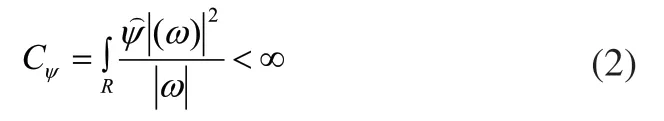
令：

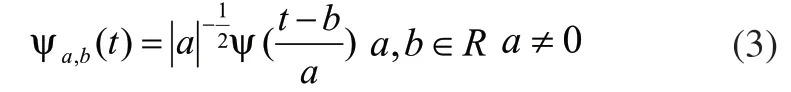
a是尺度参数，b是平移参数。连续小波的形状随着尺度函数a的变化而发生变化，连续小波的位移随着平移参数b的变化而发生变化[4]。

在这里我们对于多分辨分析的理解，用一个三层的分解来解释，小波分解树如图4所示，显然可以看到，多分辨分析仅仅对低频部分进行了再分解，而对高频部分不做任何处理。分解的关系为：S=D1+D2+D3。

图4 多分辫分析树结构图

小波包分析技术可以对频带进行多层次划分,从而可以对信号进行更细致的分析，对没有得到细分的高频信息进行精细的分解，对高频和低频成分都能够达到很精细的分析，从而提高了时频分辨率，所以小波包具有更加广泛的实用价值。

定义un(t)如下：

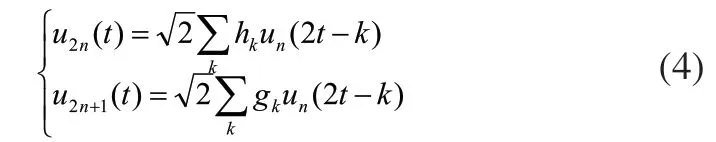
2.2 小波包基的选择

正交小波包的基一般选择具有紧支集的DB构造的正交小波。从DB小波规则性系数表中能够看出db2、db3和db4的处理效果要比db5、db6、db7等的效果好，dbN的函数的消失矩阶数为N,N越大，反映出信号高频细节的能力也就越强[5]。在汽轮机转子振动故障诊断的过程中，利用db3小波变换来对故障信号进行特征提取。

利用Daubechies小波中的db3对去噪处理后的故障振动信号进行3层小波包分解,对第3层的各个频率成分进行信号特征提取，以x30、x31、x32、x33、x34、x35、x36、x37分别表示第3层从低到高8个节点的分解系数。对各节点分解系数进行重构,可以得到与各个节点相对应的重构数据：s30、s31、s32、s33、s34、s35、s36、s37。计算各频带信号的总能量：

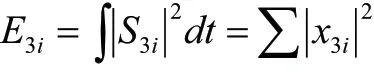
对E3i进行归一化处理：

2.3 小波包提取故障征兆表

图5为对去噪后不平衡故障采用db3小波包3层分解的各个节点重构波形图。图6为频带归一化后的能量分布树。

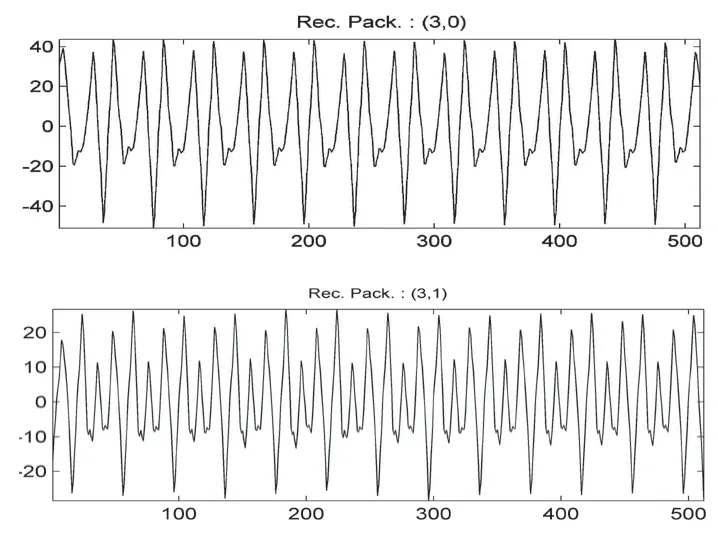
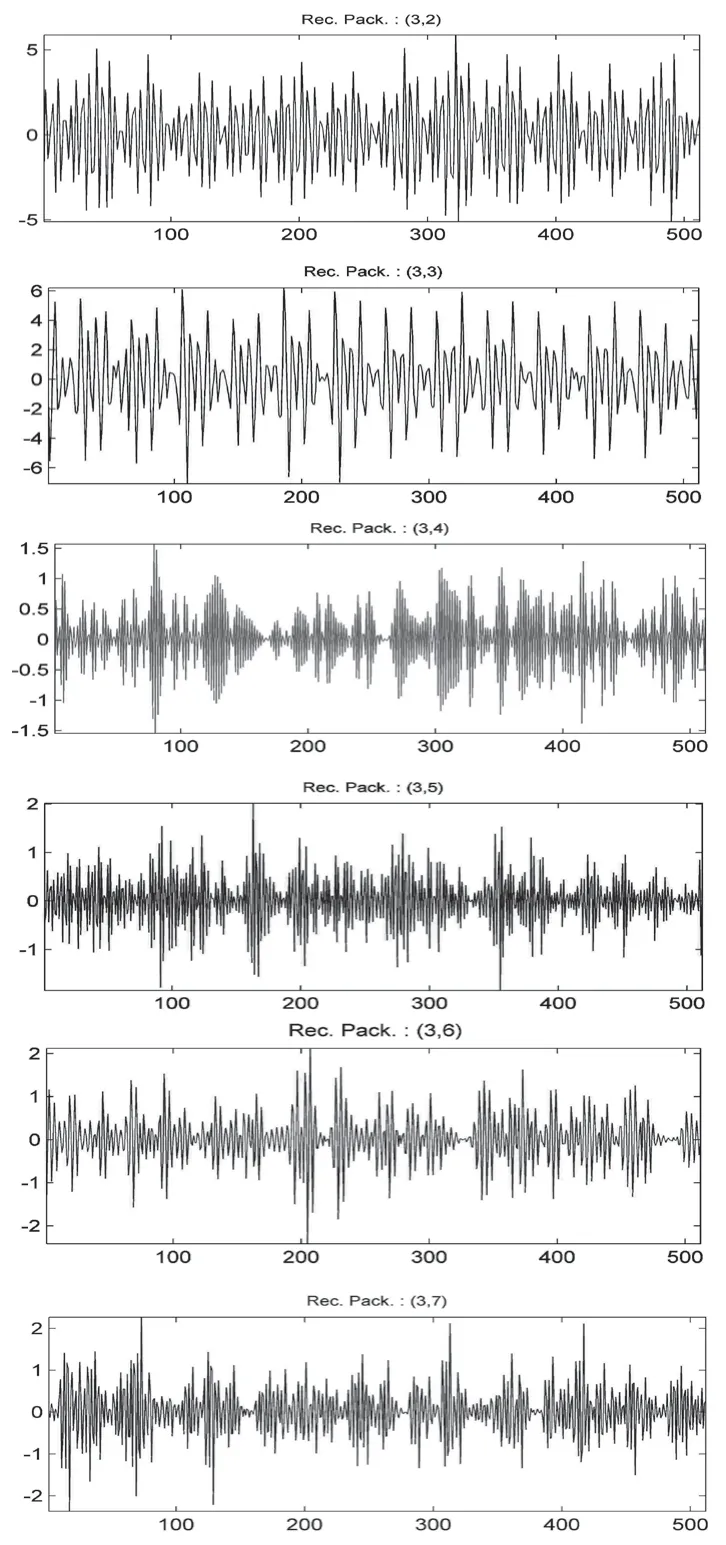
图5 不平衡振动故障各个节点重构波形图

图6 不平衡故障的能量分布树

综上所述，通过获得信号在8个频段上各自的能量，即可获得六种故障与正常态振动信号的故障征兆，如表1所示。

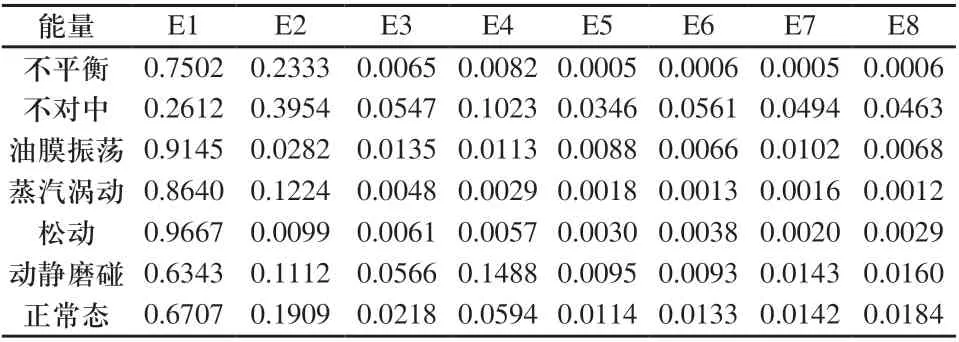
表1 汽轮机转子振动故障征兆表

3 GA-LM-BP神经网络模式识别

3.1 神经网络的改进

BP神经网络具有非线性映射能力、自学习和自适应能力。但是它同时有容易陷入局部寻优、收敛速度慢以及全局寻优能力较差等问题[6]。LM-BP神经网络提高了BP网络沿负梯度方向局部寻优的能力，克服了权值修正量小的问题,但在实际应用过程中仍不能完全克服BP算法的固有缺陷[7]。可以利用遗传算法的全局搜索能力来优化LM-BP神经网络的初始权值和阈值，从而提高网络的训练速度和识别精度[8]。

本文利用遗传算法对LM-BP神经网络连接通道的连接权值和阈值进行最优解寻优,网络模型中种群个体需要按照四个部分连接进行考虑,即：输入层与隐含层的连接权值、隐含层与输出层的连接权值、隐含层神经元间的连接阈值、以及输出层神经元间的连接阈值。染色体的编码与连接权值映射关系通常为：

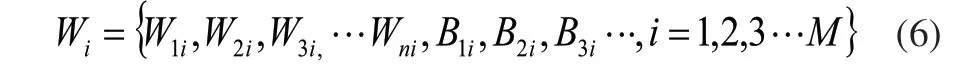
遗传算法对适应度函数的要求是：必须是单一值、连续、非负数并且最大化。因此设计其适应度函数为：

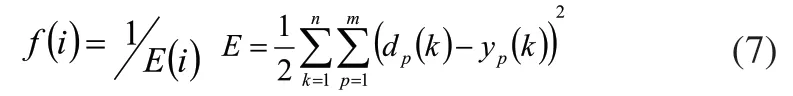
式中，dp(k)和yp(k)分别是第k个学习训练样本的目标输出值和实际输出值，n为整个网络模型训练样本的总数，M为遗传种群的规模大小，Pc为交叉概率，Pm为变异概率。经综合分析，本文取n=56、m=3、M=100、Pc=0.5、Pm=0.005。

3.2 GA-LM-BP神经网络训练结果

为了验证遗传算法在提高LM-BP网络运算速率、准确度等方面的功能，在建立网络模型输入变量与输出变量之间非线性映射关系后，通过MATLAB仿真软件对单纯弹性改进的BP网络模型、LM-BP网络模型和基于GA改进的LM-BP网络模型的误差修正综合性能进行仿真试验，仿真结果如图7所示。

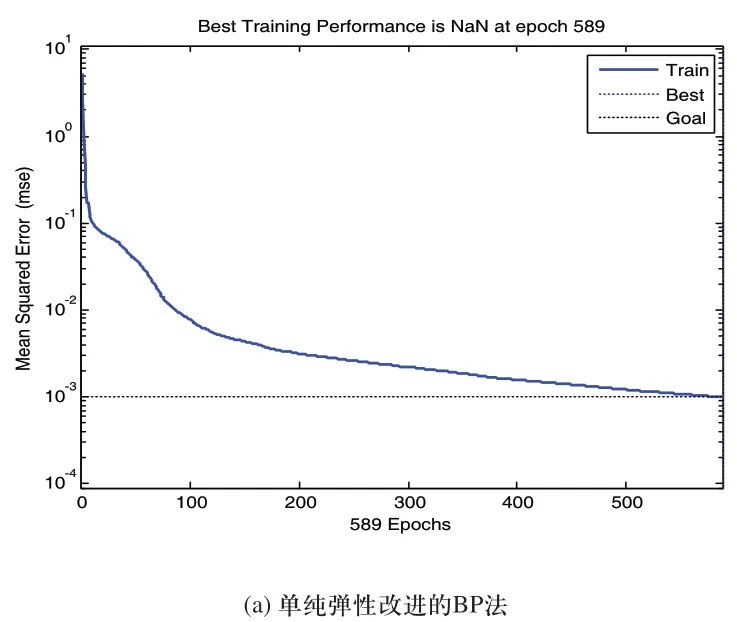
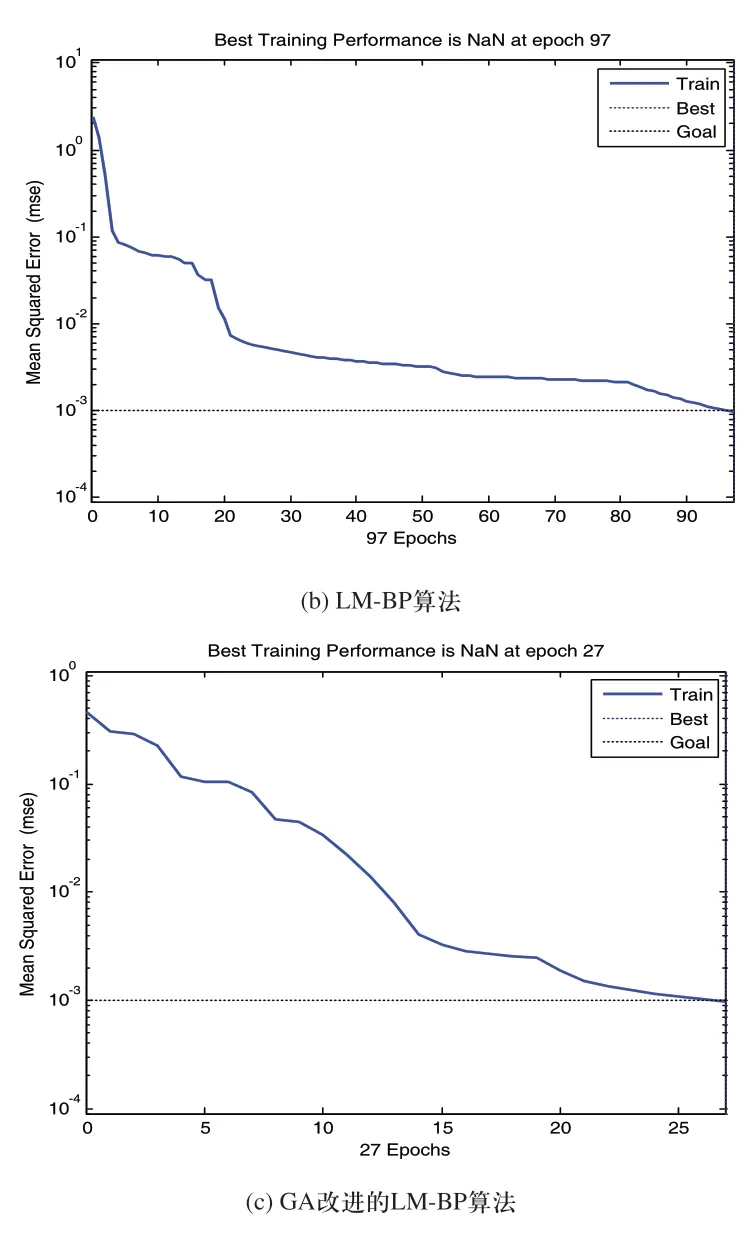
图7 不同算法网络的训练曲线

从图7中可以看出，同样的收敛精度的情况下，GA改进的LM-BP神经网络的收敛步数明显少于单纯的弹性改进法和LM-BP算法，更容易达到目标精度。且GA改进的LM-BP神经网络模型由于初始权值得到了遗传算法全局搜索的优化，所以初始的均方根误差比其他两种算法要低一个数量级，更加验证了基于GA改进的LM-BP神经网络在故障诊断方面具有显著优点。

4 诊断决策

对训练后的网络进行测试，测试结果如表2所示。

表2 网络测试结果

通过表2我们可以看到，基于GA改进的LM-BP神经网络的汽轮机故障诊断方法不仅诊断速度较改进前有了明显提高，而且诊断准确率也是相当高的。

5 结论

本文针对汽轮机转子振动故障诊断的问题，提出了小波包分析与GA-LM-BP神经网络结合的诊断算法。采用基于shannon熵的最优小波包基降噪的方法，用小波包对处理后信号进行分解与重构，从而提取各种故障的征兆；结合GA-LM-BP算法，改进了BP神经网络。研究结果显示，基于小波包分析和GA-LM-BP神经网络的故障诊断方法在信号预处理去噪方面明显优于传统的硬阈值去噪，能得到更加平滑且不失真的信号曲线；GA改进的LM-BP网络较其他网络具有迭代次数少，收敛速度快以及精确度高的特点，能够快速准确的建立起故障信息与故障模式输出之间的映射。本文提出的研究方法为汽轮机转子振动故障诊断提供了一种高效精准的可行思路，并具有一定的实用性价值。

[1] 曾秀丽,玄兆燕,于子旺.小波与神经网络结合用于电机在线监测与故障诊断[J].制造业自动化,2010,32(9)：36-38.

[2] 王波.汽轮机故障诊断技术探讨[J].机电信息,2014,15：102-103.

[3] LUO Xiangyang,LIU Fenlin,YANG Chunfang,et al.Image universal steganalysis based on best wavelet packet decomposition[J].Science China,2010,53(3)：634-647.

[4] RONG mingxing.Wavelet Transform and Neural Networks in Fault Diagnosis of a Motor Rotor[J].International Journal of Plant Engineering and Management,2012,17(2)：104-111.

[5] 吴松林,张福明,林晓东.基于小波神经网络的滚动轴承故障诊断[J].空军工程大学学报：自然科学报：自然科学报,2008,9(1)：50-53.

[6] 刘锦荣,王绍进,任芳,等.基于遗传算法优化BP神经网络的提升机制动系统故障诊断[J].煤矿机械,2011,32(5)：246-248.

[7] C Pan,W Chen,Y Yun.Fault diagnostic method of power transformers based on hybrid genetic algorithm evolving wavelet neural network[J].IET Electr. Power Appl.(S1751-8660), 2008,2(1)：71-76.

[8] 王雅娟,张滂涛.基于GA与L-M优化算法的变压器故障诊断研究[J].电子设计工程,2012,20(6)：11-15.