基于ADAMS的Mecanum八轮全向移动平台运动学分析与仿真
邢雯丽,朱建江,2
(1.中国矿业大学 机电工程学院,徐州 221116;2.常熟理工学院 电气与自动化工程学院,常熟 215500)
0 引言
全向移动平台是指在平面上具有前后、左右和中心旋转3个自由度,在不改变自身位姿的情况下可以沿任意方向进行移动的运载机构。全向移动平台的灵活机动性和精确定位,使其在船舶、仓库、航空等领域广泛应用。目前全向移动机构的应用研究主要集中在四个Mecanum轮全向移动平台[1~3]方面,然而随着航空航天器、石化、电力部组件和配套产品向更大尺寸及重量[4~6]发展,四轮全向移动平台已逐渐不能满足承受重载的使用要求。重载情况下,四轮全向移动平台需要的驱动扭矩大,且采用蓄电池直流供电,四个Mecanum轮驱动模式时,需要采用高压供电、大功率电机,因高压供电需要的电池组过多,导致整体尺寸过大且不经济。若采用低压供电(一般为48V或72V),驱动电机功率无法选的较大,否则电流过大控制电路中的功率器件不能满足要求。若选择较小功率电机、大减速比减速机来满足大扭矩,则导致全向平台运动速度过低,也不能满足使用要求。因此,对于重载全向移动平台采用多个全向轮(Mecanum轮)协同驱动技术是合理的选择。
本文提出一种由八个Mecanum轮协同驱动控制的全向移动平台,建立其运动学方程,然后运用ADAMS完成相应的运动学建模和仿真分析,得到平台沿不同方向的运动特性。
1 建立运动学数学模型
八个Mecanum轮协同驱动控制技术是全向移动平台实现重载的关键技术,其运动学方程的建立是实现其驱动控制的前提。
1.1 建立运动学二维模型
如图1所示,Oxy是与全向移动平台几何中心重合且与机身固联的直角坐标系,图中标号1~8的方框为八个全向轮,方框中斜线表示各轮与地面接触的小辊子的偏置方向。是与全向轮i轮毂中心重合且与辊子固联的直角坐标系,Ri为轮中心在平台坐标系中的位置向量,ω为全向平台绕自身几何中心的角速度,L0、L1、L2为轮中心在平台坐标系中的位置尺寸,D为全向轮直径。
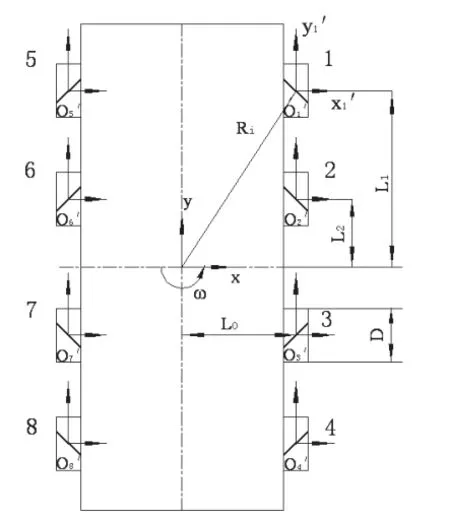
图1 Mecanum八轮全向移动平台二维模型
1.2 建立运动学方程
为建立八Mecanum轮全向移动平台的运动学方程,便于对其进行运动学分析,对全向平台的运动过程进行以下假设:
1)假设全向平台、Mecanum轮及地面均为刚体,且平台在平坦地面上运动,忽略自身结构及地面变形对其运动情况带来的影响。
2)假设轮子与地面的摩擦力足够大,轮子不发生打滑现象。
3)忽略全向轮和全向底盘在制造中的误差,假设 Mecanum轮与地面的接触点在轮心的正下方。
全向轮i的运动结构原理[7,8]如图2所示,ri为轮i与地面接触辊子的中心,si为辊子轴线方向单位向量,si与的夹角为γ, τi为垂直于si方向的单位向量,为轮i 转过的角度,为辊子转过的角度。假设辊子与地面接触点无相对滑动,则点速度可表示为:

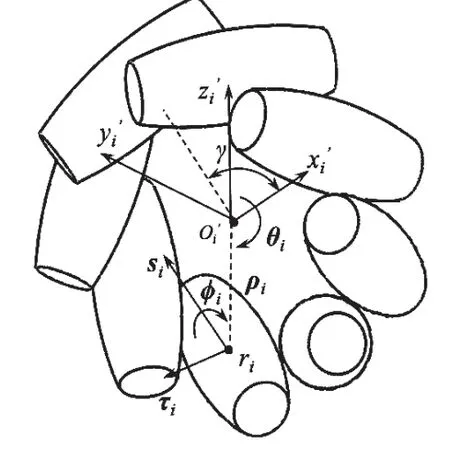
图2 轮i运动结构原理图
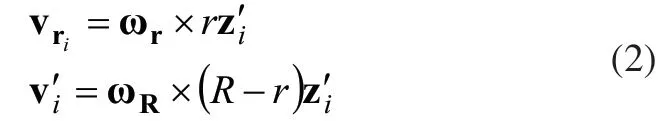
式中,z′i为Oi′zi′方向的单位向量, ωr为辊子转动角速度,ωR为轮毂转动角速度,R为全向轮半径,r为辊子的最大半径。
而根据全向平台以及全向轮的运动关系,可以得到:
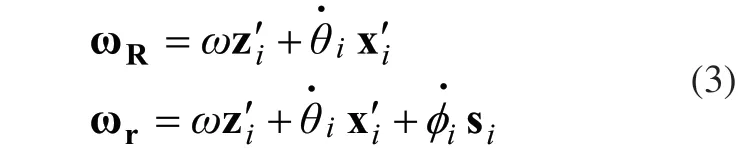
结合式(1)、式(2)以及式(3)可以得到:
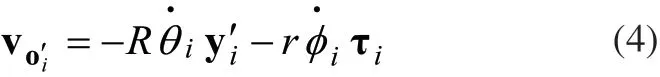
从另一个角度来看,根据图1所示,点iO′速度在全向平台中可以表示为:
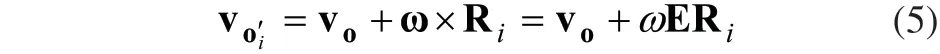
式中,vo为全向平台几何中心速度,E为变换矩阵:

其作用是使Ri逆时针旋转90°。
由矢量的定义,有:
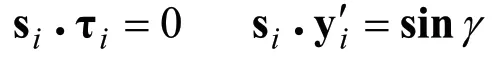
则将式(4)、式(5)两边同时点乘si,联立后得到:
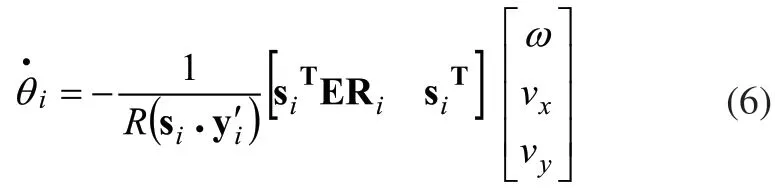
综合八轮的全向移动平台,展开后的运动学方程式如下:

对应两种辊子安装角度的全向轮如图3所示,有si.y'i=cos45°或者si.y'i=cos135°,以此确定相应的γ值。
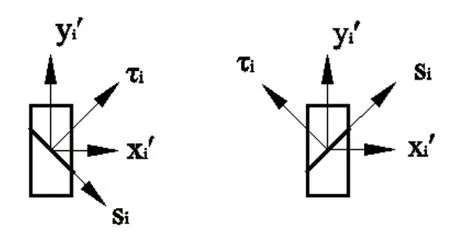
图3 两种辊子安装形式
则式(7)可简化为:
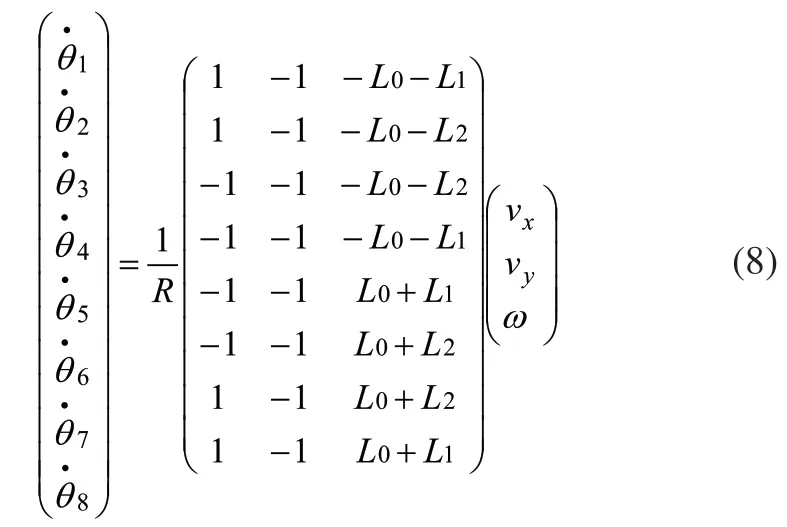
式(8)为平台的逆运动学方程,设:
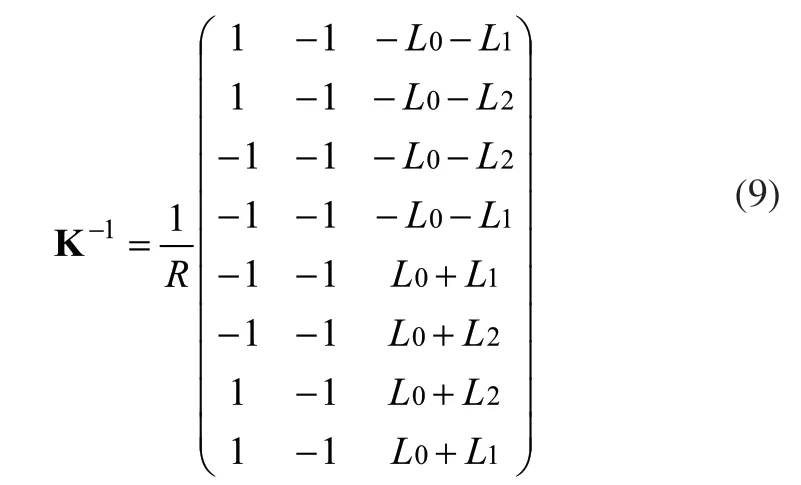
式中,K-1为系统速度的逆雅可比矩阵。rank(K-1)=3,是实现平台全方位运动必要条件。全向平台的正运动学方程为:

2 建立仿真模型及参数设置
本文以KUKA公司型号为KoM UTV-2 E375的全向移动平台结构参数为依据,结合自身载荷特点确定了Mecanum八轮全向移动平台整体结构参数,其主要参数如表1所示。

表1 Mecanum八轮全向移动平台参数
利用SolidWorks软件进行全向移动平台三维模型的创建,然后将模型导入ADAMS软件中,再根据全向平台的约束关系及运动形式添加约束及运动副,完成全向平台虚拟样机的建模。建立全向平台的三维模型时,在满足全向平台虚拟样机仿真结果准确性的前提下,简化了全向平台机械结构的细节设计、省略了与其运动无关的部件。
由于对全向平台的运动学进行仿真时,主要考虑Mecanum八轮系统的运动情况,因此将全向平台车体部分作为一个整体零部件,省略其中的悬挂结构。而电机及减速机的传动则由软件中设置的驱动副取代。图4为简化后的全向平台装配图。
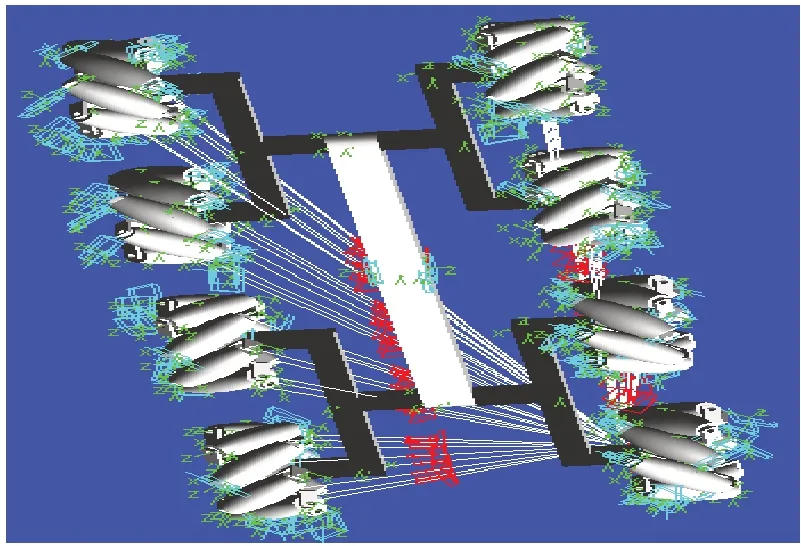
图4 全向移动平台简化三维模型
将建立好的三维模型导入ADAMS中,对软件进行基本设置,单位选择为MMKS,设置重力加速度为9.8m/s2,定义各部分材料属性。然后,定义模型的运动副与约束关系。在车身与轮毂轴线、辊子轴线与轮毂之间添加旋转副;在辊子与地面之间添加接触关系,根据全向平台运动时Mecanum轮各辊子与地面接触方式的特点,定义辊子与地面为断续接触,在ADAMS中采用冲击函数法(Impact)模拟辊子与地面的接触,采用库伦法(Coulomb)模拟辊子与地面的摩擦。根据现有的研究文献[9~11]及工程实践,定义函数中各参数值,如表2所示。
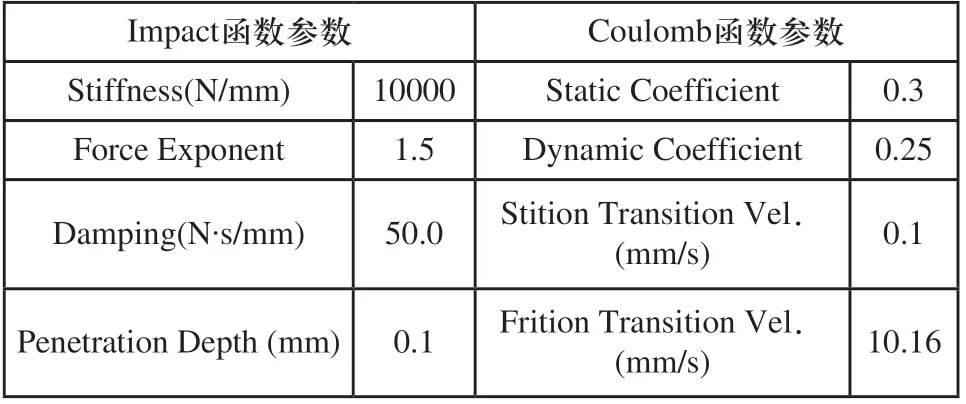
表2 ADAMS接触函数参数设置
3 仿真结果与分析
3.1 全向平台+x向运动仿真
对全向平台沿x正向运动进行仿真,定义平台移动速度为220mm/s,无y向及转动速度。根据式(8)全向平台的运动学方程计算得到八个Mecanum轮的转速分别如表3所示。在虚拟样机中对八个Mecanum轮添加对应的旋转驱动,得到仿真结果如图5所示。
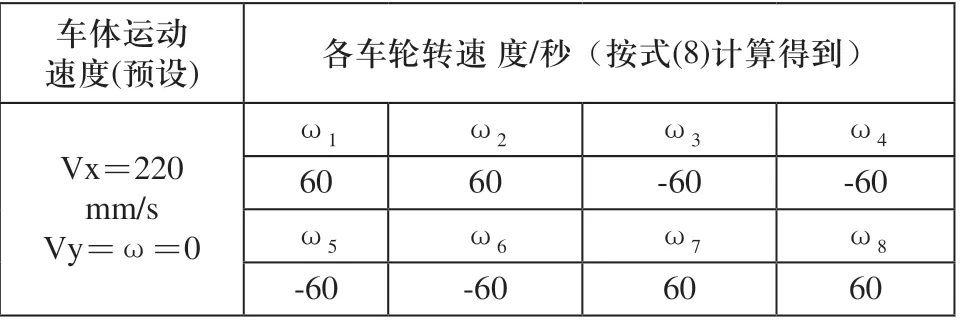
表3 +x方向各轮转速
图5所示为全向平台几何中心沿x正向的运动速度,可以看出平台运动速度经过一个上升阶段,这是平台从静止状态开始加速的过程,然后达到相对稳定阶段,约为220mm/s,但是运动过程中存在一个很小的速度波动。出现这样速度波动的原因是在Mecanum轮转动过程中,多个辊子与地面交替接触使得接触条件随之不断变化。
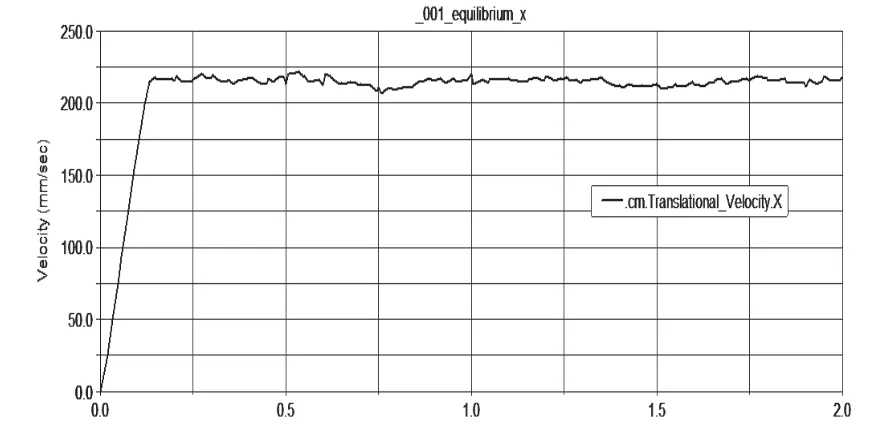
图5 +x方向运动仿真
3.2 全向平台沿45度方向运动仿真
对全向平台沿45度方向运动进行仿真,定义平台x、y正向移动速度均为110mm/s。根据式(8)全向平台的运动学方程计算得到八轮的转速如表4所示。在虚拟样机中对八个Mecanum轮添加对应的旋转驱动,得到仿真结果如图6所示。
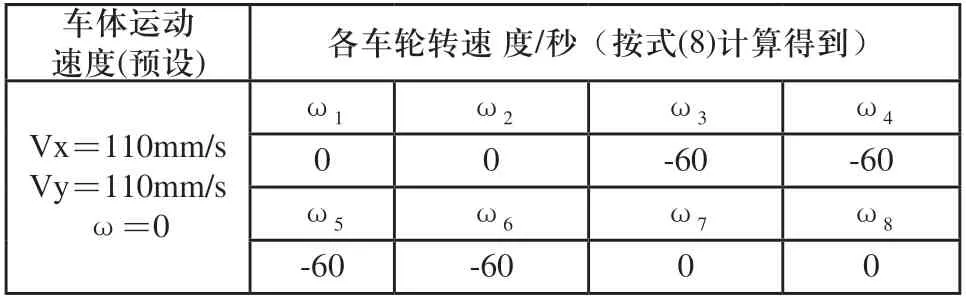
表4 45度方向各轮转速
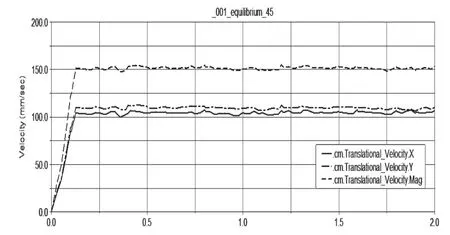
图6 45度方向运动仿真
图6所示为全向平台几何中心沿45度方向的运动速度,可以看出,平台x,y向运动速度基本稳定在110mm/s,合成速度经过上升阶段达到110×=155.56mm/s,相对稳定后也存在一个很小的速度波动。出现这样波动的原因是除了沿x向运动造成的波动外,采用椭圆近似曲线制造辊子,使得Mecanum轮的包络面并不是标准的圆柱面,沿y向运动时速度也会有存在一定的波动,可以看出沿y向的速度波动较x方向平缓一些。
3.3 全向平台绕自身几何中心旋转运动仿真
对全向平台绕自身几何中心旋转运动进行仿真,定义平台转动角速度为-21rad/s,无x、y向移动。根据式(8)全向平台的运动学方程计算得到八轮的转速分别如表5所示。在虚拟样机中对八轮添加对应的旋转驱动,得到仿真结果如图7所示。

表5 绕自身几何中心转动方向各轮转速
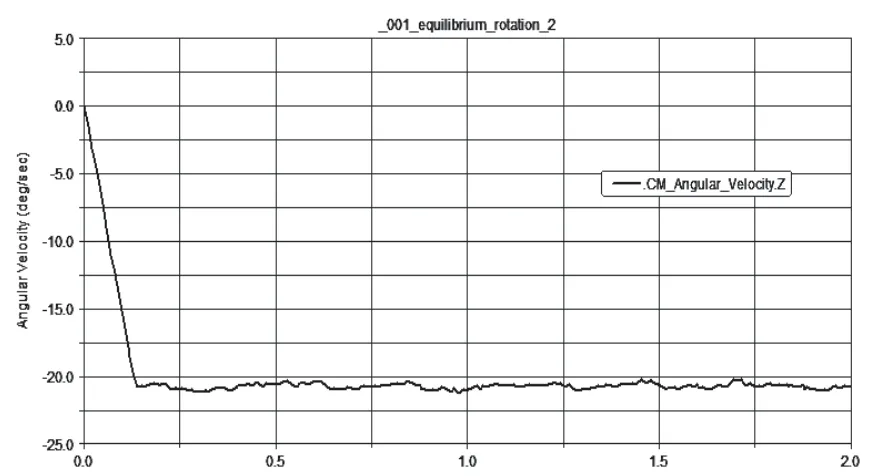
图7 绕自身几何中心转动方向仿真
图7所示为全向平台绕自身几何中心转动角速度,其角速度值经过下降阶段到达相对稳定后存在较为平缓的速度波动,稳定值约为-21rad/s。
3.4 45度方向运动,同时绕自身转动
对全向平台沿45度方向运动同时绕自身几何中心旋转进行仿真,定义平台x、y正向移动速度为110mm/s,转动角速度为-21rad/s。根据式(8)全向平台的运动学方程计算得到八轮的转速如表6所示。在虚拟样机中对八轮添加对应的旋转驱动,得到仿真结果如图8所示。
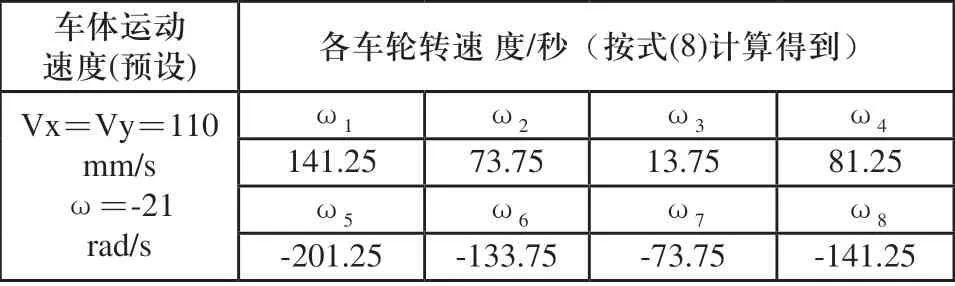
表6 45度方向运动,同时绕自身几何中心转动各轮转速
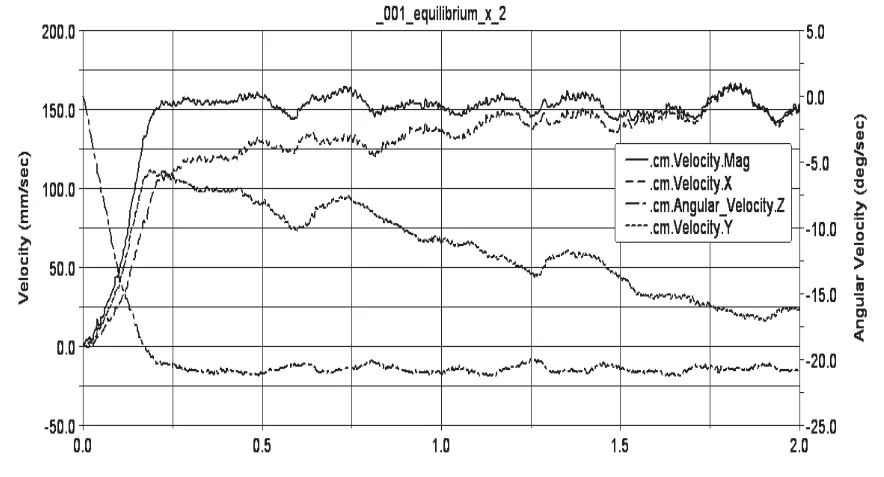
图8 45度方向运动,同时绕自身几何中心转动仿真
图8所示为全向平台沿45度方向同时绕自身几何中心旋转的运动速度,仿真得到转动速度约为-21rad/s,x和y方向初始速度为110mm/s,当平台绕自身转动一定角度后,平台的平移速度方向与绝对坐标系不再呈45度夹角,而是在x和y绝对坐标系下的分量值进行变化,但是可以得到平台的速度合成值不变约为155.56mm/s。
4 结论
1)为适应大型精密产品向更大尺寸及重量发展的趋势,本文提出了一种由八个Mecanum轮协同驱动控制的全向移动平台,建立了其运动学模型,推导了其运动学方程。
2)在ADAMS软件中建立了全向移动平台的简化虚拟样机模型,通过仿真分析,得到了平台沿+x方向、45度方向、绕自身几何中心转动方向以及沿45度同时绕自身转动方向的运动规律。
3)仿真所得结果与理论计算值基本一致,说明参数设置合理,同时验证了运动方程的正确性。该运动学方程的建立解决了研发八Mecanum轮全向移动平台的一个关键技术问题,为以后动力学和运动控制的研究奠定了基础,对重载全向移动平台的研发具有一定的参考价值和工程意义。
[1] 关利赢,郝鑫,常力欣,等.万向电动叉车螺旋滚轮轮体设计[J].军事交通学院学报,2009,11(2):65-68.
[2] 吕伟文.全方位轮移动机构的结构设计[J].机械与电子,2006,(12):63-65.
[3] 石维亮,王兴松,贾茜.基于Mecanum轮的全向移动机器人的研制[J].机械工程师,2007,(9):18-21.
[4] 邹丹,马向莉.全向轮智能移动平台前景展望[J].军民两用技术与产品,2012,2:56-58.
[5] 许国康.大型飞机自动化装配技术[J].航空学报,2008,29(3):734-740.
[6] 吴晓峰,赵祉江,柳权.大空间尺寸测量及大部件运输、跟踪、定位技术[J].航空制造技术,2009,24:38-41.
[7] 王一治,常德功.Mecanum四轮全方位系统的运动性能分析及结构形式优选[J].机械工程学报,2009,45(5):307-310.
[8] 贾官帅.基于Mecanum轮全方位移动平台的理论和应用研究[D].杭州:浙江大学,2012:1~56.
[9] 李敏.全向剪叉自行式高空作业平台的开发[D].南京:南京航空航天大学,2013:1-70.
[10] 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006.
[11] 赵武云,刘艳研,吴建民,王芬娥.ADAMS基础与应用实例教程[M].北京:清华大学出版社,2012.

