一种新的Kohonen神经网络结构优化方法

付 琦

（山东农业工程学院，济南 250100）

0 引言

Kohonen网络是T. Kohonen教授于1981年首次提出的，是一种由具有自调整功能的神经元组成的人工神经网络[1]。Kohonen采用自动分类算法，又称自组织特征映射神经网络，是自组织映射（Self-Organising Maps，SOM）思想的起源[2]。网络的各个神经元之间通过相互的侧向交互作用进行竞争，以近邻者相互激励、远邻者相互抑制的规则自适应地组织而形成针对特殊信息的一个组织结构[3,4]。这种单层无监督学习算法可看成是模式识别和自动分类算法的一种拓展，训练阶段对SOM算法的性能具有重大影响，所以Kohonen网络架构的选择是神经网络研究的一个重要方面[5]。近年来，学术界对人工神经网络架构的优化问题，尤其是Kohonen网络架构的优化问题，开始进行研究[6～8]。

本文从混合整数角度对非线性约束条件下的Kohonen网络架构优化问题进行建模。本文模型的成本函数包括两项：第1项控制几何误差并构建拓扑顺序；第2项控制拓扑映射的规模。本文模型可对Kohonne网络架构进行优化，以该模型为基础，通过在最小化阶段定义一种学习规则，提出了一种新的学习分类方法。由于连续Hopfield网络（Continuous Hopfield Network，以下简称CHN网络）可有效解决优化问题，所以在分配阶段采用了CHN网络[8]。

1 连续Hopfield网络建模

1.1 连续Hopfield神经网络简介

CHN网络由Hopfield和Tank提出，是一种结合存储系统和二元系统的神经网络，用于解决组合优化问题[9,10]。近年来，CHN网络在图像处理、模式识别、生产调度优化以及机器人路径规划领域获得广泛应用[11～13]。CHN由带有平滑s形激活函数的互连神经元构成，描述CHN网络动态特性的微分方程如下：

其中y、v和Ib分别表示神经元状态、输出和偏差向量。输出函数vi=g(yi)为双曲正切函数，下界为0、上界为1。实数值Ti,j和Iib分别表示从神经元i到j的突触连接的权重及神经元i的偏置。除此之外，Hopfield还引入了[0,1]n上的能量函数E，定义如下：

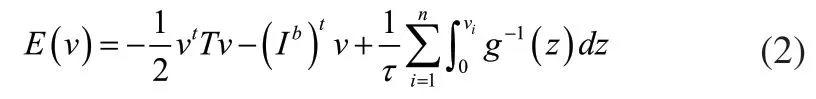
如果能量函数E存在，则平衡点也存在[9]。为基于CHN网络求解组合优化问题，这里将能量函数E(v)进行简化，如式(3)所示。

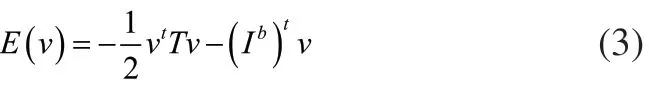
1.2 优化模型

为了考虑成本函数、分配约束和传输约束等条件，定义式(4)，既可对使用的神经元数量进行优化，又可保持观测集上定义的领域概念。

2 优化训练方法

因为优化问题(P)是带有多项式目标函数的混合整数问题，所以我们分两步求解该问题：

分配阶段：我们固定权重向量然后求解如下问题：整数变量下的多项式分配问题。

最小化阶段：我们固定分配向量然后求解如下问题：连续变量条件下的非线性优化问题。

在迭代之前，我们固定第t-1次迭代时获得的权重向量，并利用CHN网络求解如下整数变量条件下的优化问题：

为了利用CHN网络求解(Pt)问题，需要构建合适的能量函数，如式(6)所示：

考虑到u是CHN网络的神经元输出，I是网络偏差，T是能量函数为时网络中链路的权重函数，则第(n+1)N个神经元间链路的权重为：

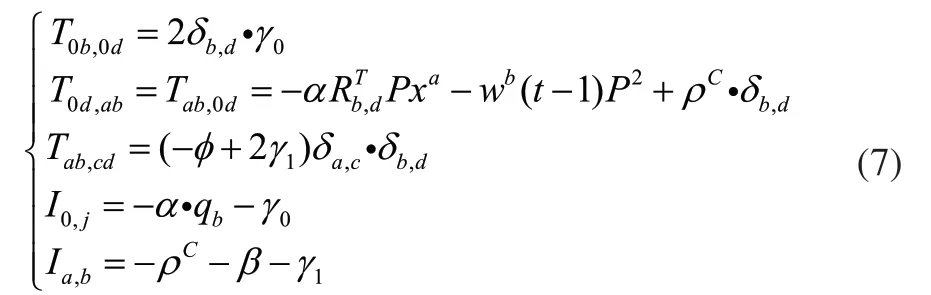
式(8)是约束条件 成立的充分条件：

式中的参数约束条件为：

其中：

利用式(9)可以将约束条件简化，如下式所示：

已知描述空间和Kohonen拓扑映射的尺寸后，我们通过求解确定最终的参数。在最小化阶段，需要固定变量向量u，以此求解连续变量条件下的优化问题，只需要保证在每次迭代时只使用一种简单的梯度方法即可：

其中，wj(t)表示第t次迭代过成中j的重心。以文献[14]中的算法为基础，结合式(7)、式(9)、式(10)、式(11)，提出优化训练算法如图1所示，其中初始化过程包括定义输入变量，以及输出变量。计算参数值过程包括：根据方程(7)计算T和I，根据方程(9)计算M1和M2，根据方程(10)计算

图1 优化算法流程图

3 仿真试验

为了阐述Kohonen优化架构的优点，我们对得到广泛应用的Iris虹膜分类数据集运行本文算法，共包括3种目标类型：Setosa（Se），Virginica（Vi）和Versicolor（Ve）。每种类别包括50个数据样本。在训练前，利用如下规则对数据进行正规化：

一半数据（75个，每种25个）样本用于训练，另外一半用于测试。为了对Iris数据进行聚类，随机选择映射的初始尺寸，该尺寸由本文模型目标函数的项控制。表1给出了映射尺寸和迭代次数不同时剩余神经元的均值。通过表1可以看出，对Iris数据进行聚类时神经元数量基本收敛于11。

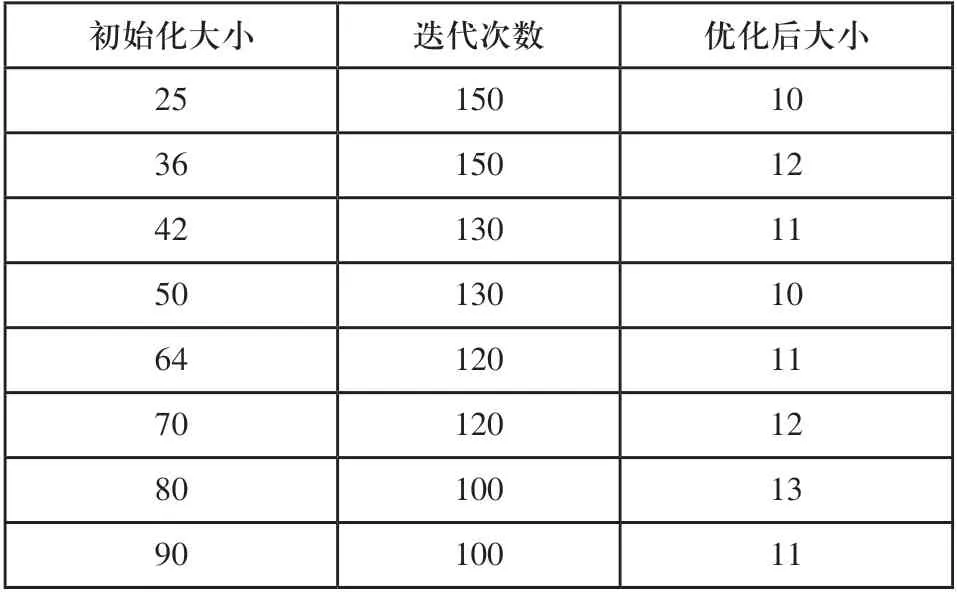
表1 最佳神经元数量选择表

本文方法使Kohonen学习算法更加完整，实际上，本文方法同时提出两个任务：学习任务以及使映射尺寸最小的优化任务。通过3个步骤实现这些目标：分配步骤，决策步骤及最小化步骤。通过这种方法，我们在收敛时只获得有用神经元，简化了标识任务。

表2给出了训练数据的聚类结果，可以看出，本文方法的结果较优，仅有2个数据没有被成功分类，其他数据均被正确分类。错误分类的数据来自Versicolor类别。

表2 测试数据分类的数值仿真结果

图2和图3分别从不同角度将本文提出的算法与传统的EPB、RBF以及SVM等算法进行对比，图2为不同算法在计算耗时（单位为s）以及迭代次数方面的对比情况，图3给出了不同算法分类结果的成功率情况。

图2 不同算法的对比（耗时与迭代次数）

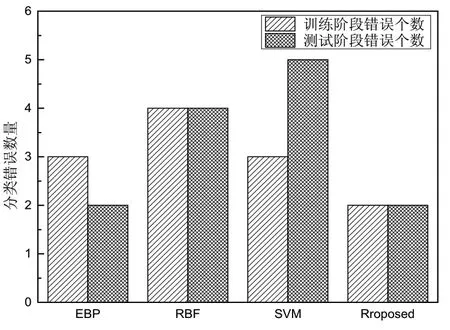
图3 不同算法对比（成功率）

通过图2可以看出，四种算法当中，表现较差的是EBP算法，该算法的迭代次数和计算耗时均比较高，RBF和SVM算法分别在迭代次数和计算耗时单方面表现突出，而本文提出的算法同时具有较短的计算耗时（9.5s）和较少的迭代次数（150次），因此，相比而言，本文优化后的算法结果表现更优。除此之外，通过图3的分类准确率也可以表明，本文提出的方法具有较高的准确率。

4 结论

本文从非线性约束条件下的混合整数优化问题角度，对Kohonen架构的选择问题进行建模。提出了一种新的模型，以该模型为基础，通过给出最小化阶段的学习规则，提出一种学习分类算法，从而优化Kohonen网络架构。与Kohonen经典学习算法相比，本文提出的方法可避免映射中的非无用神经元。为了进一步阐述本文方法的优点，我们对Iris常用分类数据集运行本文方法。实验结果证明了本文方法的优点，尤其是本文方法在分类质量和架构映射优化方面的优势非常明显。与EBP、RBF和SVM等方法相比，本文方法可在较短时间内给出高质量分类结果。下一步，我们将把本文方法用于图像压缩和语音处理领域。

[1] Kohonen T.Self-organized formation of topologically correct feature maps[J].Biological Cybernetics.1982,43(1)：59-69.

[2] Chung-Chian H, Shu-Han L.Visualized Analysis of Mixed Numeric and Categorical Data Via Extended Self-Organizing Map[J].Neural Networks and Learning Systems, IEEE Transactions on.2012,23(1)：72-86.

[3] 方浩,王艳红.改进的Kohonen神经网络航迹关联算法[J].计算机应用.2013,(05)：1476-1480.

[4] 麻书钦.基于Kohonen神经网络算法的网络入侵聚类算法的测试研究[J].中国测试.2013,(04)：113-116.

[5] 李厚强,刘政凯,林峰.基于分形理论和Kohonen神经网络的纹理图像分割方法[J].计算机工程与应用.2001,(07)：44-46.

[6] Chung-Chian H.Generalizing self-organizing map for categorical data[J].Neural Networks, IEEE Transactions on.2006,17(2)：294-304.

[7] Talaván P M, Yáñez J.The generalized quadratic knapsack problem.A neuronal network approach[J].Neural Networks.2006,19(4)：416-428.

[8] Ettaouil M, Elmoutaouakil K, Ghanou Y.The continuous hopfield networks(CHN) for the placement of the electronic circuits problem[J].W.Trans. on Comp.2009,8(12)：1865-1874.

[9] Ghosh A, Pal N R, Pal S K.OBJECT BACKGROUND CLASSIFICATION USING HOPFIELD TYPE NEURAL NETWORK.

[10] J. J. Hopfield P O T N.Neurons with graded response have collective computational properties like those of two-states neurons[C].Proceedings of the National Academy of Sciences,USA,1984.

[11] 张志新,张明廉.基于并行混沌和单纯形法的混合全局优化算法[J].系统仿真学报.2004,(01)：35-37.

[12] 修春波,刘向东,张宇河.双混沌机制优化方法及其应用[J].控制与决策.2003,(06)：724-726.

[13] Steck J E, Balakrishnan S N.Use of Hopfield neural networks in optimal guidance[J].Aerospace and Electronic Systems,IEEE Transactions on.1994,30(1)：287-293.

[14] Talaván P M,Yàñez J.A continuous Hpfield network equilibrium points algorithm[J].Computers and operations research.2005,(32)：2179-2196.