星型齿轮箱启动扭矩分析与计算

冯 金

（中航商用航空发动机有限责任公司，上海 201108）

0 引言

高涵道比双转子涡轮风扇发动机自上世纪70年代初投入使用以来，受风扇叶尖切线速度限制，与风扇相连的低压压气机与低压涡轮只能在较低转速运行，从而导致压气机级数增多，重量大且效率低。为解决上述问题，可在由低压压气机及低压涡轮组成的低压转子与风扇转子间安装一套合适的风扇驱动齿轮箱（Fan Drive Gear System,FDGS），使风扇转子工作于低转速，而低压转子工作于高转速，即为齿轮传动涡扇发动机（Geared Turbofan，GTF）。相比船舶及风电等其它领域，航空领域中特别是涡扇发动机中所使用的风扇驱动齿轮箱具有载荷大转速高的特点，设计难度较大，虽然在国外已相对成熟[1,2]，但在国内依然处于理论研究阶段[3, 4]。

根据风扇与低压轴之间传动比要求的不同，风扇驱动齿轮箱多采用单级行星或星型轮系。能够满足星型齿轮传动系统试验要求的试验装置形式多样，大体可分为开放功率流试验台及封闭功率流试验台两种[5]。开放功率流试验台通常由原动机、试验件和负载三部分组成，功率由原动机提供，经过试验件传递至负载，故而能量损失较大。为了避免开放功率流试验台能耗较大的缺点，对于传递功率较大的星型齿轮箱，通常使用封闭功率流试验台进行试验。按照其加载方式的不同，又可分为电加载功率封闭试验台[6]、机械加载功率封闭试验台及液压加载功率封闭试验台[7]三种类型。对于齿轮传动涡扇发动机星型风扇驱动齿轮箱，由于其传递功率大，输入转速高，故通常采用液压加载功率封闭试验台进行试验。进行试验台设计时，不但电机的功率需要大于整个封闭系统的功率损失，当带载启动时电机的启动扭矩也要大于整个封闭系统的启动扭矩。对于封闭功率流试验台，工程中通常取电动机的功率为封闭功率的8%至15%，但在试验过程中经常会出现由于电机启动扭矩过小而使整个封闭系统无法启动的情况。为避免临时加装盘车所带来的不便，在进行试验台设计时就需要对封闭系统的启动扭矩进行计算。

为进一步开展风扇驱动齿轮箱研制工作，本文以五路分流人字齿星型风扇驱动齿轮箱为研究对象，分析惯性力矩、滑动摩擦力矩及滚动摩擦力矩三方面因素对星型齿轮箱试验件启动扭矩的影响。

1 星型齿轮箱试验件结构

五路分流人字齿星型风扇驱动齿轮箱试验件主要由太阳轮、行星轮、外齿圈、轴承、行星架及传扭支架等零组件构成，如图1所示。太阳轮为浮动构件，作为输入端与输入轴通过花键连接，并与五个均匀分布的行星轮相啮合；每个行星轮采用齿轮轴承一体化设计，由双列调心滚子轴承在内部支撑，与外齿圈相啮合；外齿圈为浮动构件，作为输出端通过螺栓与输出轴连接；整个齿轮箱的重力及齿轮啮合时产生的扭矩通过行星架由传扭支架承受。

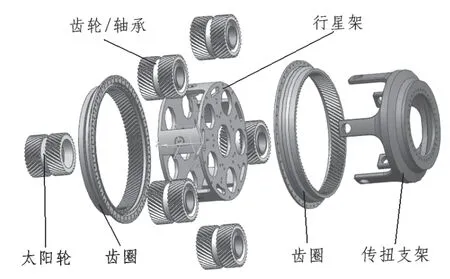
图1 星型齿轮箱试验件结构图

2 液压加载功率封闭试验台原理

液压加载功率封闭试验台原理图如图2所示，星型齿轮箱试验件与陪试件以“背靠背”方式组合，两个星型齿轮箱的输出轴通过联轴器相互相连，两个星型齿轮箱试验件的输入轴通过两个跨接齿轮箱与加载器相连。加载器工作时其左右两端输出轴具有反向转动的趋势，从而使所有齿轮相互啮合产生扭矩。电动机通过增速箱与其中一个跨接齿轮箱相连，从而带动由星型齿轮箱试验件、陪试件、两个跨接齿轮箱以及加载器组成的功率闭环。

图2 液压加载功率封闭试验台原理图

进行试验台设计时，不但电动机的功率需要大于整个封闭系统的功率损失，当带载启动时电动机的启动扭矩同样需要大于整个封闭系统的启动扭矩。由于齿轮传动链启动扭矩计算方法大致相同，故本文仅对星型齿轮箱试验件本身的启动扭矩进行分析，不考虑功率闭环中其余部件的影响。

3 启动扭矩计算方法

星型齿轮箱试验件的启动扭矩Tg可以分为三部分，分别为惯性力矩Tm、轮齿滑动摩擦力矩Tsf以及轴承摩擦力矩Trf。惯性力矩用来克服各个齿轮轴自身的转动惯量；轮齿滑动摩擦力矩用来克服各齿轮齿面的静滑动摩擦力；轴承摩擦力矩用来克服各轴承转动时的滚动摩擦力。

1）惯性力矩

设太阳轮齿数为zs，绕其旋转轴的转动惯量为Js；行星轮齿数为zp，绕其旋转轴的转动惯量为Jp；外齿圈齿数为zr，绕其旋转轴的转动惯量为Jr；星型齿轮箱启动时其输入轴角加速度为α。则整个星型轮系绕太阳轮旋转轴的等效转动惯量为sJspr，如下所示：

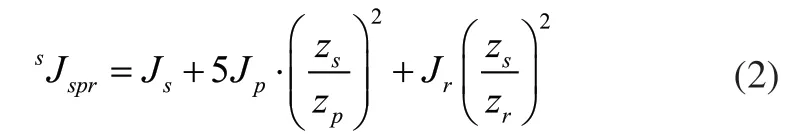
假设星型齿轮箱试验件输入轴角加速度α为恒定值，则星型齿轮箱试验件启动时所需克服的惯性力矩如下所示：

2）轮齿滑动摩擦力矩

设太阳轮分度圆直径为ds，基圆直径为dbs；行星轮分度圆直径为dp，基圆直径为dbp；外齿圈分度圆直径为dr，基圆直径为dbr；各齿轮分度圆法向压力角均为na，螺旋角为β，模数为m，齿面静滑动摩擦系数为fs；通过加载器加载在太阳轮上的扭矩为sTl，只考虑惯性力矩的影响而不考虑轴承摩擦力矩的影响时，太阳轮与行星轮之间的圆周力为，法向力为；行星轮与齿圈之间的圆周力为，法向力为

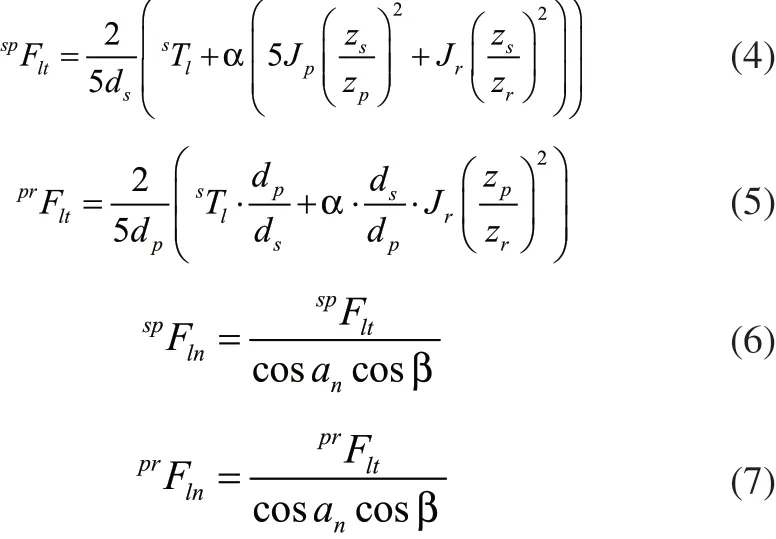
令作用在太阳轮与行星轮啮合齿面上的法向力所产生的静摩擦力为，作用在太阳轮与行星轮啮合齿面上的法向力所产生的静摩擦力为，由上式可知：

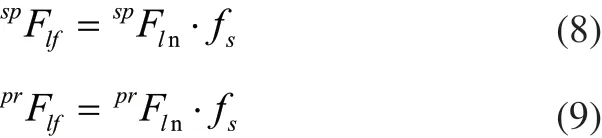
根据渐开线圆柱齿轮齿廓公式可知，啮合时摩擦力相对齿轮轴线的力臂大小随着啮合点的变化而变化。为方便计算，此处取啮合点位于分度圆时的力臂，则与作用在太阳轮与行星轮啮合齿面上的静摩擦力相对应的力臂为，与作用在太阳轮与行星轮啮合齿面上的静摩擦力相对应的力臂为

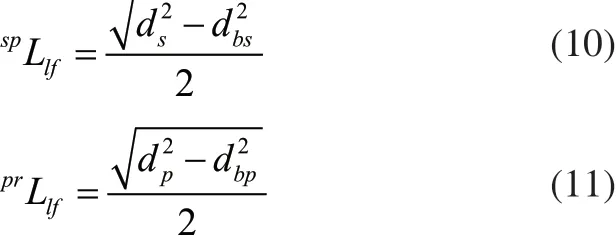
由此可知，电机启动时克服星型齿轮箱试验件齿面静滑动摩擦力所需要的扭矩Tsf为：

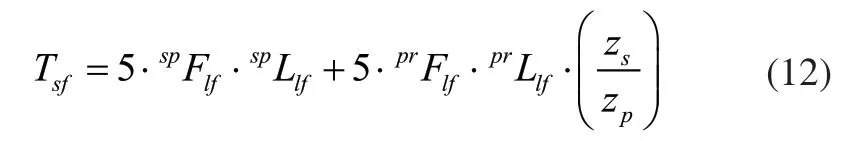
3）滚动轴承摩擦力矩

滚动轴承摩擦力矩的计算采用Palmgren方法，分为外加载荷引起的摩擦力矩M1和润滑剂粘性摩擦力矩M0两部分。滚动轴承的总摩擦力矩M为：

上式中M0与轴承类型、转速和润滑油性质有关，当v.n＜2000时：

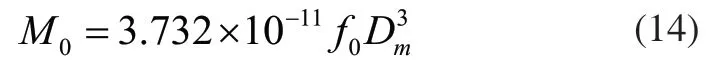
其中n为轴承转速，v为滑油运动粘度，Dm为轴承节圆直径，f0为与轴承类型和润滑方式有关的系数。

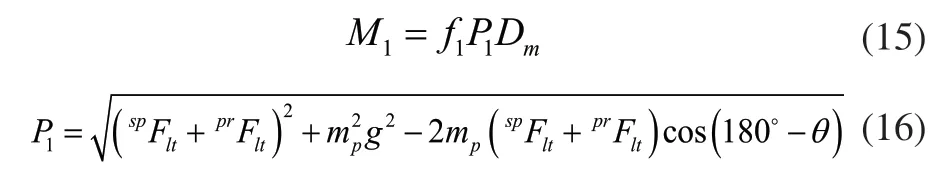
其中f1为与轴承类型和所受负载有关的系数；P1为确定轴承摩擦力矩的计算负载，受到重力、惯性力矩及滑动摩擦力矩的共同影响；mp为行星轮质量；θ为行星轮所受圆周力与重力之间的夹角，每个星型齿轮箱包括5个滚动轴承，其对应夹角θ分别为0°、72°、144°、-144°和-72°。故作用在滚动轴承上的摩擦力矩等效到太阳轮上的力矩为：

4 启动扭矩分析

根据上述启动扭矩计算方法，现以某星型齿轮箱试验件设计参数为例进行启动扭矩计算，分析输入轴角加速度α与加载器加载扭矩slT对启动扭矩的影响。各齿轮轮齿参数如表1所示，轴承节圆直径Dm为86mm，与轴承类型和润滑方式有关的系数f0为10，与轴承类型和所受负载有关的系数f1为0.00045，滑油动力粘度v为5mPa·s。

表1 某星型齿轮减速器轮齿参数表

当输入轴角加速度α为30r/s2时，随着加载器加载扭矩的增加，惯性力矩Tm、滑动摩擦力矩Tsf、滚动摩擦力矩Trf及启动扭矩Tg的变化如图3所示。由下图可知，惯性力矩不随加载扭矩发生变化；滑动摩擦力矩随加载扭矩增大而大幅增加，滚动摩擦力矩随加载扭矩增大的增幅较小可以忽略；当加载扭矩低于280N.m时，启动扭矩大于15%加载扭矩的经验值上限，当加载扭矩大于280N.m时，启动扭矩小于15%加载扭矩的经验值上限。

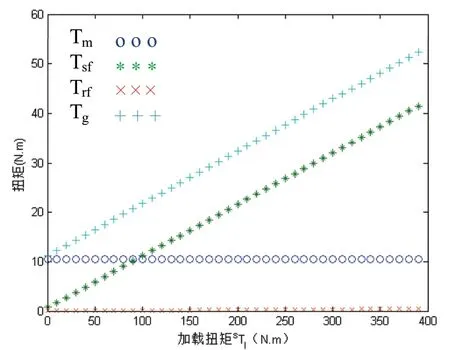
图3 扭矩随加载扭矩变化示意图

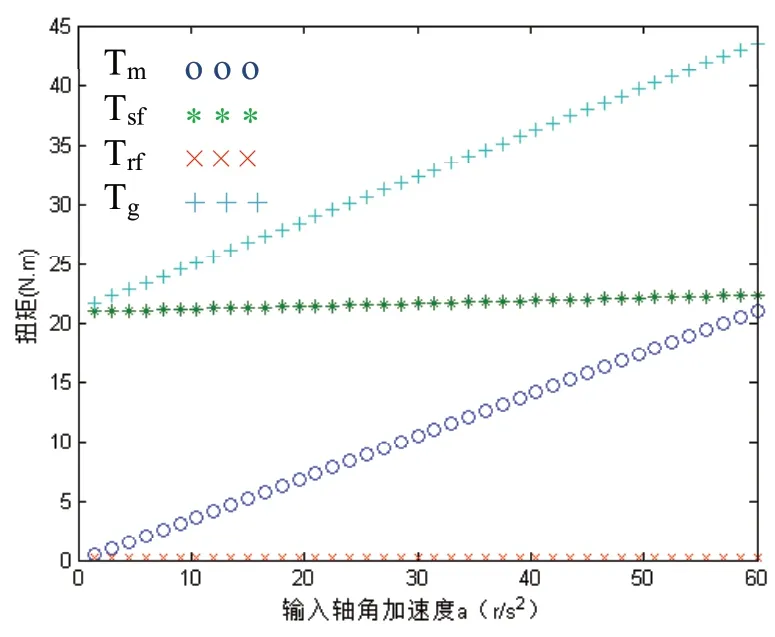
图4 扭矩随角加速度变化示意图

5 结论

本文以齿轮传动涡扇发动机五路分流人字齿星型风扇驱动齿轮箱为研究对象，从惯性力矩、滑动摩擦力矩及滚动摩擦力矩三方面对齿轮箱试验件的启动扭矩进行分析。计算结果表明，滚动摩擦力矩在启动扭矩中占比很小；惯性力矩受输入轴角加速度影响较大，滑动摩擦力矩受加载器加载扭矩影响较大；随着输入轴角加速度或加载器加载扭矩的组合变化，启动扭矩有可能超过经验值规定范围。

[1] 陈光.齿轮传动风扇 PW8000高涵道比涡轮风扇发动机[J].民航经济与技术,1998(5)：37-39.

[2] 聂晶,杨瑾,童悦.大型民机发动机关键技术现状与发展趋势[J].航空制造技术,2012(21)：34-37.

[3] 陈聪慧,信琦.风扇齿轮驱动系统的概念设计[J].航空科学技术, 2011.4：005.

[4] 侯明曦.GTF发动机行星齿轮传动系统设计技术研究[J].航空发动机,2014.40(2)：61-64.

[5] 齿轮手册编委会.齿轮手册（第2版）[M].机械工业出版社.2013.

[6] 汤建晖.电功率封闭试验技术在传动台的应用[A].中国航空学会第十六届机械动力传输专业委员会学术论文交流会议[C].2013：393-402.

[7] 杨兵华.直升机主减行星轮系试验器研制[A].中国航空学会第十六届机械动力传输专业委员会学术论文交流会议[C].371-377.