对角修形斜齿轮径向剃齿设计

蒋进科，方宗德，彭先龙

（西北工业大学机电学院，710072西安）

对角修形斜齿轮径向剃齿设计

蒋进科，方宗德，彭先龙

（西北工业大学机电学院，710072西安）

为减小齿轮振动与噪音，设计对角修形斜齿轮齿面，根据啮合原理推导其径向剃齿刀齿面；根据齿条展成渐开线齿面原理，结合Y7432平面砂轮磨齿机，建立有齿向平移运动的平面砂轮磨齿CNC模型；建立基于CNC机床各轴及砂轮轴向廓形敏感性分析的齿面修正模型，各轴运动用6阶多项式表示，分析0阶及1阶系数变化对齿面误差的影响；通过判断砂轮与剃齿刀齿面的接触状态，确定磨削齿面的误差，以误差平方和最小为目标函数，采用粒子群优化算法，得到机床各轴运动及砂轮轴向廓形参数.结果表明:该算法计算结果稳定，降低了磨削误差；对角修形斜齿轮的径向剃齿刀拓扑修形曲面基本为齿向反鼓形与对角修形曲面叠加；沿齿向方向的压力角、展成运动角、螺旋角参数微调可分别实现一定的对角修形加工；砂轮增加齿向运动构成3轴联动，减小了砂轮半径，可用于磨削大螺旋角、大齿宽对角修形斜齿轮.

斜齿轮；对角修形；数控磨削；径向剃齿；平面砂轮；敏感性分析；高阶校正

斜齿轮对角修形主要用于减小啮入啮出冲击和承载传动误差，降低传动系统振动与噪音［1］，与传统的齿廓、齿向修形相比，可以保证齿轮副有较高重合度和接触区宽度，提高了承载能力，对于提高航空、航海高速齿轮系统的性能有重要意义.

剃齿与磨齿是先进的齿轮精加工工艺.通过剃齿、磨齿工艺可实现对角修形斜齿轮加工.国内外学者对剃齿技术研究取得了一定成果，剃齿在汽车制造业中已得到了广泛应用.刘俐平等［2-4］介绍了径向剃齿刀的齿形计算、刃磨及切削槽排列工艺.詹安东等［5］通过计算普通剃齿刀和齿轮之间齿面相对滑动速度的变化及齿面诱导法曲率的变化，分析齿形中凹现象原因.王素玉等［6］通过解析计算对径向剃齿的齿形中凹现象进行了分析.王宪法［7］将平面砂轮修整成外锥面，磨削径向剃齿刀，实现了窄斜齿轮对角修形加工，但方法尚未公开.为了减小振动与噪音，Fuentes、Litvin等［8-9］分别设计加工修形渐开线圆柱齿轮的径向剃齿刀、轴向剃齿刀，并进行齿面接触分析（tooth contact analysis，TCA）仿真.

随着三坐标测量技术及多轴数控技术的发展，对轮齿精度要求越来越高，上述传统的剃齿刀齿面设计方法需要改进.

Free-Form型数控机床及基于三坐标测量的齿形拓扑误差技术，曾应用于螺旋齿锥齿轮等复杂齿面的加工及检测，现已被借鉴应用于圆柱齿轮.Liu等［10］通过分步优化锥面砂轮锥角及砂轮轴向廓型，磨削径向剃齿刀，加工拓扑修形圆柱齿轮；Hsu等［11-14］分析锥面砂轮参数及其安装参数对径向剃齿刀齿形拓扑误差影响；此外，对径向剃齿刀切削的平稳性以及刀槽设计进行了优化与分析，还分析了轴向剃齿加工鼓形齿时，机床附加鼓形机构的运动参数与工件鼓形量关系.Radzevich［15-16］根据工件拓扑修形齿面，通过一种改进的运动学方法，进行径向剃齿刀拓扑修形齿面计算；并将该改进的运动学方法应用于成形砂轮磨削拓扑修形径向剃齿刀时的砂轮轴向廓形参数计算，但该方法具体不详.秦傲然等［17］给出了径向剃齿刀齿数的计算公式、切削刃排列方式，总结了轴交角的选取与加工质量之间的关系.王沁等［18］通过优化径向剃齿刀拓扑修形齿面离散点的误差最小得到磨削剃齿刀的锥面砂轮安装参数.Shih等［19］提出一种5轴联动圆柱齿轮成形磨齿高阶校正技术，建立基于5轴运动及砂轮轴向廓型的齿面误差敏感性分析方程组，通过最小二乘法获得机床各轴及砂轮廓型参数，其关键技术是齿面误差敏感矩阵的计算及超定方程组求解，但实际上对于高精度圆柱齿轮，随着三坐标测量齿面网格点数据的增加，该方程组的高度病态，其求解精度降低，工程应用受限.蒋进科、方宗德等［20-22］曾对基于敏感矩阵的多轴联动数控磨齿求解方法进行了一定的仿真研究，主要是针对鼓形齿或可解析表达法向修形曲面的圆柱齿轮.然而，径向剃齿刀齿面是一个中凹的扭曲双曲面，对于加工对角修形斜齿轮齿面的径向剃齿刀，其齿面更为复杂，必须要建立基于齿面坐标测量的径向剃齿刀修形齿面模型与多轴数控高阶磨齿加工模型，为径向剃齿设计与制造提供理论依据.

为此本文设计小轮对角修形齿面，求解其径向剃齿刀拓扑修形量；结合Y7432平面砂轮磨齿机，建立平面砂轮磨齿CNC模型及修形砂轮轴向廓型和各轴6阶多项式的齿面修正模型，对文献［19］中的求解方法进行改进，通过粒子群（particle swarm optimization，PSO）优化方法，得到各轴运动参数及砂轮参数，有效降低了磨削误差.该方法可用于磨削对角修形斜齿轮径向剃齿刀及对角修形斜齿轮，磨削剃齿刀时，砂轮固定，进行2轴联动高阶校正；磨削斜齿轮时，砂轮增加齿向运动进行3轴联动高阶校正.

1 对角修形斜齿轮设计及径向剃齿刀拓扑修形曲面计算

1.1 对角修形齿面设计

斜齿轮对角修形区域见图1，仅对啮入啮出端进行修形，中间部分不修或者少修，修形区域为△abc和△def，Ⅰ为沿接触线上修形量相等，Ⅱ为沿接触线修形量不相等.修形齿面位矢与法矢为

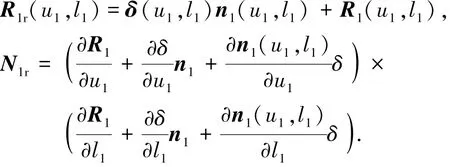
图1 对角修形区域示意

式中:R1、n1分别为小轮理论齿面位矢、单位法矢，R1r、n1r分别为小轮修形齿面位矢，法矢；δ为修形量，u1、l1分别为渐开线齿面参数.

对角修形曲面设计的关键是确定修形量，修形量的大小与齿轮承受的载荷及齿轮的误差有关，理想的修形量是齿轮在进入啮合时没有冲击，平稳接触，具体方法见文献［23］.

1.2 径向剃齿刀拓扑修形曲面计算

径向剃齿的加工近似于一对相错轴渐开线圆柱齿轮传动，剃齿刀螺旋角与工件的螺旋角形成一个轴交角如图2所示，仅沿工件径向方向进给运动，剃齿刀齿面是与工件渐开线螺旋面做交错轴啮合的共轭齿面，根据微分几何求解包络面如下所示:

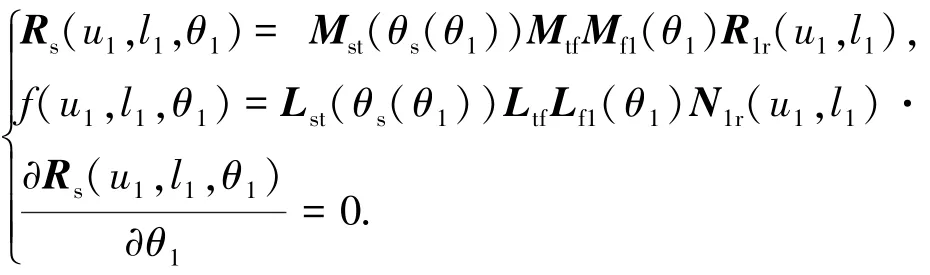
式中:θ1为工件转角，θs=iθ1为剃齿刀转角，i为传动比；Sf、S1分别为工件参考、运动坐标系；St、Ss分别为剃齿刀参考、运动坐标系；Mst、Mtf、Mf1、Lst、Ltf、Lf1分别为从工件齿面到剃齿刀齿面位矢及法矢变换矩阵.

径向剃齿刀齿面虽然已经不是渐开线螺旋面，但与理论渐开线螺旋面仅差几十μm，其法向修形量表示为

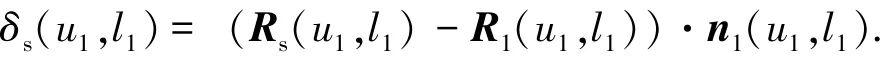
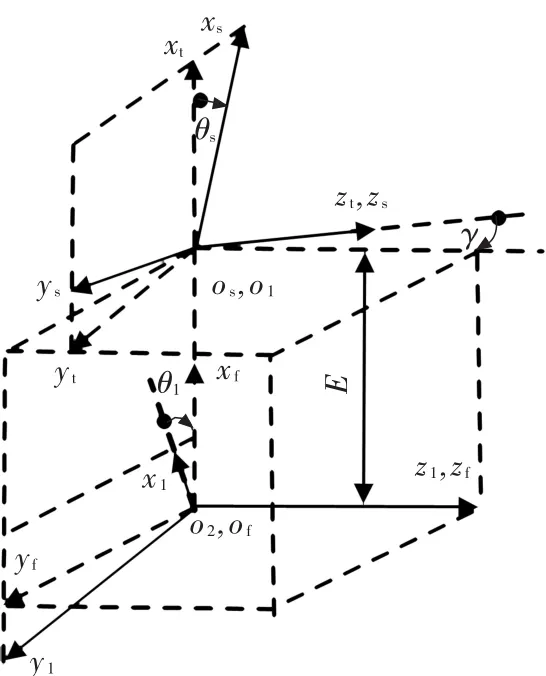
图2 径向剃齿安装坐标系

2 平面砂轮CNC磨齿模型及机床运动参数计算

2.1 平面砂轮CNC磨齿模型

如图3（a）所示，为了可以磨削大螺旋角、大齿宽斜齿轮且不至于划伤齿根，平面砂轮模拟齿条且可以沿齿向平移运动如图3（b）所示，砂轮展成渐开线齿面表示为

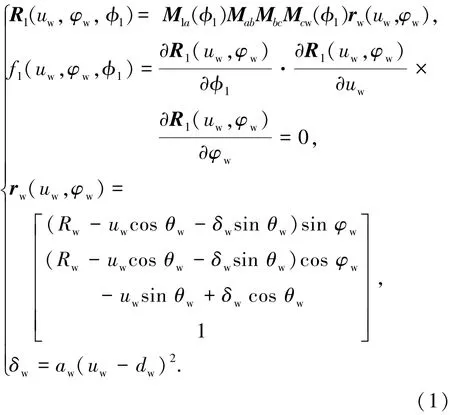
式中:rw（uw，φw）为砂轮位矢，uw、φw为砂轮参数，Rw为外径参数，θw、aw、dw为砂轮轴向廓形修形量δw的参数；Sf、S1分别为工件参考、运动坐标系，原点在工件齿宽中部，回转轴为x轴；Sw、Sc为平面砂轮运动坐标系及参考坐标系；Sa，Sb分别为分度圆螺旋角β与法向压力角αn的参考坐标系；φ1为工件展成角，M1a、Mab、Mbc、Mcw为从砂轮到齿面的变换矩阵，图3（b）中Cs为砂轮沿齿条齿向运动速度常参数.

结合Y7432磨齿机，建立图3（c）所示数控机床模型，其坐标系如图3（d）所示，根据齿轮啮合原理，考虑到平面砂轮边界，磨削后的齿面位矢:

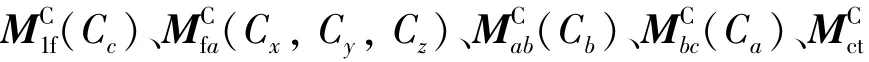
图3 平面砂轮CNC磨齿坐标系

从传统型机床向Free-Form型机床的运动等效转换原则是保证刀具与工件的相对位置和姿态在任意时刻都相同，即 （R1=R），通过式（1）～（2）得

式中:rj为工件节圆半径；rf为砂轮有效工作面外径至工件轴的距离；mn为工件法向模数；C（k=x、y、z、a、b、c）为各轴运动表达式（理论齿面），可见砂轮沿齿向运动分解在展成运动轴及轴向运动轴上，当Cs=0表示砂轮固定.

2.2 平面砂轮最小半径计算

平面砂轮与斜齿轮或径向剃齿刀瞬时接触线为直线.

1）磨削斜齿轮时，砂轮沿齿向运动，为了不至于划伤齿根，其有效外径应径向进给到工件过度曲线，且不小于最长的瞬时接触线长度ls，如图3（b）所示，且

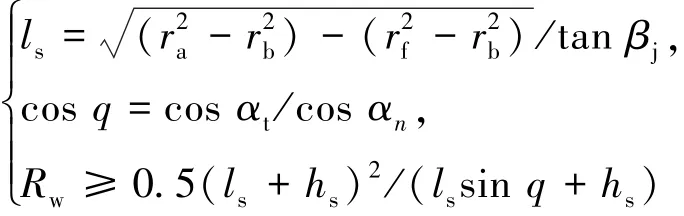
2）磨削剃齿刀时，砂轮通常固定，因此其直径应大于法向齿宽:

修形曲面是微调加工理论齿面各轴运动及砂轮轴向廓形参数的结果，选取理论展成角φ1为各轴之间的联系参数，实际加工中φ1为时间的线性函数，最高次数6阶，修形曲面表示为

即

其中:ζ为各轴运动参数系数 ζj（j= 1，…，q，q= 6×7+3= 45即a0x、a1x、…、a5c、a6c、θw、aw及dw）组成的列向量；S为齿面敏感矩阵，由网格节点i（i=1，…，p，p为齿面网格点数，取5×9=45）处各轴敏感系数组成的行向量Si构成；δ（ui，θi）为齿面网格节点i处修形量，通过对角修形曲面得到.

2.3 机床运动各轴参数求解

通过PSO优化算法［24］求解式（4）超定线性方程组，可得到机床运动参数及平面砂轮修形参数.径向剃齿刀磨削属于减材料（Ease-Off）加工，因此对砂轮是否与齿面接触做出判断:Siζ＜0表示平面砂轮嵌入刀具i点进行磨削；Siζ≥0表示砂轮远离刀具i点进行磨削；以设计变量为ζi（i= 1，…，q），刀具齿面磨削误差平方和最小为优化目标，即

由图5可知，修正前，研究区热水中文石、方解石、白云石均处于过饱和状态，白云石随温度升高，有向非饱和区过渡的趋势，石英及玉髓均处于非饱和状态；修正后，研究区热水中矿物收敛于一个较小的范围内，由图可知，ZGJ02收敛于121.6 ℃～137.7 ℃的温度区间，ZGJ04收敛于165.4 ℃～183.6 ℃的温度区间。

磨削后的剃齿刀法向修形量、加工误差及各轴附加运动为

其中:δC、Δδ、ΔCk为CNC磨削修形量、误差及各轴运附加运动量，Ck、C为CNC加工修形齿面与理论齿面的各轴运动曲线，n为理论齿面单位法矢量.

3 算例与分析

标准安装的工件、刀具参数见表1，取K1= K2=0，理论计算的剃齿刀在齿宽范围内接触线长度为75.3 mm.hs=2 mm时，砂轮无齿向运动，即Cs=0时，Rw＞320 mm；当砂轮沿齿向运动，且Cs=-8时，Rw＞230 mm.仿真分析如下.

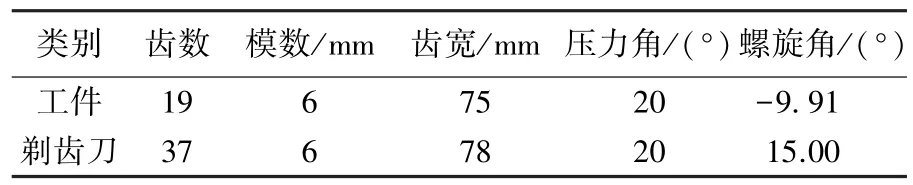
表1 工件、剃齿刀基本参数

3.1 剃齿刀齿面验证

表2为以文献［10、11］参数为例，砂轮不同安装参数时，磨削的径向剃齿刀理论齿面的修形量.

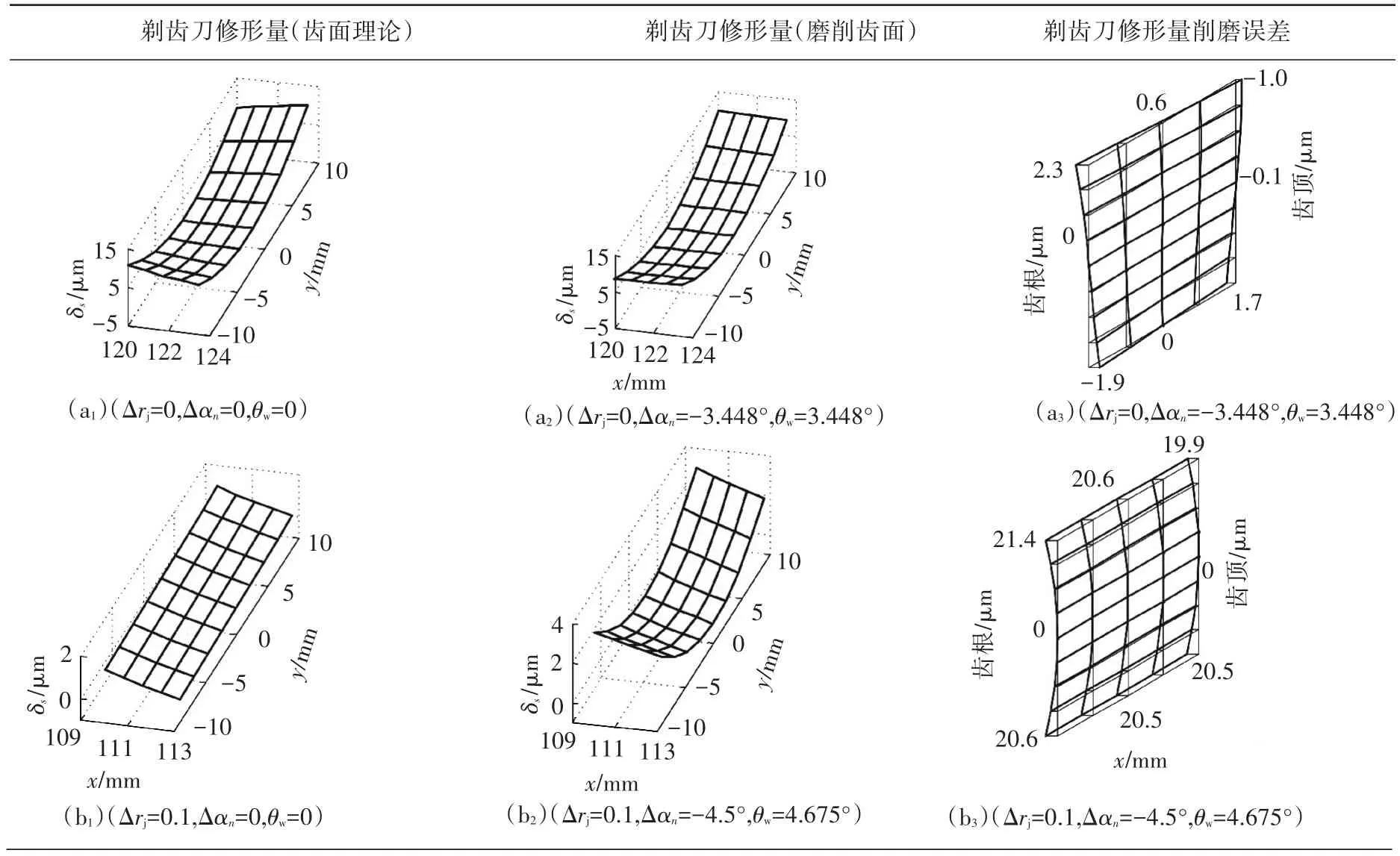
表2 平面砂轮锥底角、安装压力角及节圆半径对径向剃齿刀齿面修形量影响

标准安装的剃齿刀理论齿面为反鼓扭曲面（见（a1）），调节砂轮锥底角等于安装压力角后，可实现渐开线齿面的齿向修形（见（a2）），其与剃齿刀理论齿面误差（见（a3））与文献11中图1结果一致；

非标准安装的剃齿刀理论齿面主要为齿廓修形（见（b1）），调节砂轮锥底角与安装压力角后，磨削的渐开线齿面修形量见（b2），其与剃齿刀理论齿面误差（见（b3））与文献 10中图10结果一致.

3.2 敏感性分析

文中仅列出部分轴的扰动误差，用于剃齿对角修形齿面的附加运动分析.

压力角（Ca）、展成运动（Cc）1阶系数变化产生啮入端或啮出端对角修形（见表3（a3）、（a4）、（b3）、（b4）），其2阶系数即抛物线变化将导致啮入端与啮出端对角修形；

砂轮锥底角、轴向廓型变化产生齿廓、齿向修形（见表3（c1）、（c2）、（c3）、（c4）），当砂轮安装压力角修正量等于砂轮锥底角时，则表现为齿向校正（见（c2））.

3.3 机床运动分析

考虑到剃齿刀结构特点及机床实际运动，取Cs=0，Rw=350 mm，除了展成运动轴进行高阶校正，其余轴仅进行0阶校正.某工况下斜齿轮对角修形曲面见图4（a）.根据啮合原理，用径向剃齿刀剃削工件属于二次包络，不希望工件上出现啮合界限，通过TCA分析可知，接触线布满整个工件齿面（见图4（b）），剃齿效果将为良好；该对角修形斜齿轮反算的剃齿刀齿形修形量基本特征为:齿向反鼓形与对角修形曲面叠加，图4（c1）为剃齿刀齿面比标准渐开线齿面多出的部分，图4（c2）为留有余量的标准渐开线齿面应该去除掉的材料；优化后的解在200代后趋于稳定 （见图4（d）），其中，CNC磨削后的修形曲面较为光滑（见图4（e）），磨削误差＜2 μm（见图4（f））；各轴附加运动（见图4（g））:Cx、Cy、Cz、Cb基本趋于0，表明对角修形主要由其他2个轴及修形砂轮锥底角完成加工；Ca变化为0阶、其中0阶系数变化引起齿厚校正见表3（a2）；将Cc变化向下平移（忽略齿厚校正，因为是在留有齿厚余量的渐开线齿面进行材料分析），则实际展成角数值上总是滞后理论展成角，即砂轮远离啮入（见表3 （b4））、啮出端（见表3（b3）），因此ΔCc变化表明剃齿刀啮入、啮出端去除材料较少，其他部位去除材料较多，与剃齿刀修形曲面特征基本一致，各轴运动曲线如表4，径向剃齿修形曲面主要为0阶校正及1阶校正.

图4 平面砂轮CNC磨削对角修形斜齿轮径向剃齿刀齿面优化结果

表3 砂轮轴向廓型及机床各轴0阶、1阶误差引起法向偏差（减材料分析）

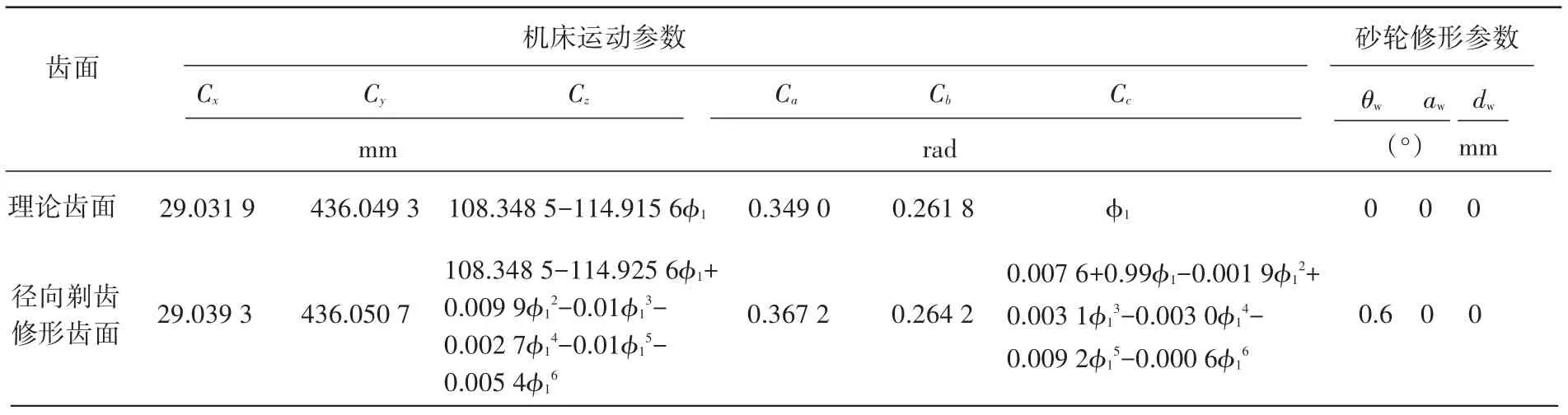
表4 C N C机床各轴运动及砂轮轴向廓型曲线

4 结 论

1）设计对角修形斜齿轮齿面（工件），推导径向剃齿刀齿面，结合Y7432磨齿机，建立有齿向平移运动的平面砂轮磨齿CNC模型.

2）建立基于修形平面砂轮轴向廓形和各轴6阶校正的齿面敏感性分析校正模型，通过优化方法，得到机床运动参数及砂轮廓形参数，有效降低了磨削误差；展成角、压力角及螺旋角微调可实现斜齿轮齿面一定的对角修形.

3）对角修形斜齿轮径向剃齿刀齿面基本为齿向反鼓形与对角修形曲面叠加的复杂曲面，可通过修正砂轮锥角、机床压力角及展成运动进行磨齿校正.砂轮增加齿向运动构成3轴联动，减小了平面砂轮半径，可应用于Y7432磨齿机3轴联动CNC再制造，磨削大螺旋角、大齿宽对角修形斜齿轮.

［1］王宪法，李华敏.窄斜齿轮对角修形的最佳修形量计算及修形区域的选择［J］.哈尔滨工业大学学报，1993，25（5）:62-66.

［2］刘俐平，李华敏.径向剃齿刀切削槽的合理排列［J］.哈尔滨工业大学学报，1997，29（6）:109-111.

［3］刘俐平，李华敏.径向剃齿刀的刃磨［J］.机械传动，1997，21（4）:34-36.

［4］刘俐平，李华敏.径向剃齿刀的齿形分析［J］.齿轮，1987（1）:5-9.

［5］詹东安，任济生，王素玉，等.随机修形剃齿刀消除剃齿齿形中凹的机理研究［J］.西安交通大学学报，1999，33（8）:45-47.

［6］王素玉，于涛，孙景友.径向剃齿刀在机修磨原理解析［J］.计算机械工程学报，2005，41（4）:162-167.

［7］王宪法.窄斜齿轮对角修形的研究［D］.哈尔滨:哈尔滨工业大学，1992.

［8］FUENTES A，NAGAMOTO H，LITVIN F L，et al.Computerized design of modified helical gears finished by plunge shaving［J］.Computer Methods in Applied Mechanics and Engineering，2010，199（25）:1677-1690.

［9］ LITVIN F L，FAN Q，VECCHIATO D，et al.Computerized generation and simulation of meshing of modified spur and helical gears manufactured by shaving ［J］.Computer Methods in Applied Mechanics and Engineering，2001，190（39）:5037-5055.

［10］LIU J H，HUNG C H，CHANG S L.Design and manufacture of plunge shaving cutter for shaving gears with tooth modifications［J］.The International Journal of Advanced Manufacturing Technology，2009，43（9/10）: 1024-1034.

［11］HSU R H，FONG Z H.Topographic error analysis of a gear plunge shaving cutter finished by a cone grinding wheel［J］.Journal of the Chinese Institute of Engineers，2006，29（3）:481-491.

［12］HSU R H，FONG Z H.Even contact design for the plunge shaving cutter［J］.Mechanism and Machine Theory，2010，45（8）:1185-1200.

［13］HSU R H，FONG Z H.Serration design for a gear plunge shaving cutter［J］.Journal of manufacturing science and engineering，2011，133（2）:1-11.

［14］HSU R H，FONG Z H.Analysis of auxiliary crowning in parallel gear shaving［J］.Mechanism and Machine Theory，2010，45（9）:1298-1313.

［15］RADZEVICH S P.Design of shaving cutter for plunge shaving a topologically modified involute pinion［J］.Journal of Mechanical Design，2003，125（3）:632-639.

［16］RADZEVICH S P.Computation of parameters of a form grinding wheel for grinding of shaving cutter for plunge shaving of topologically modified involute pinion［J］.Journal ofmanufacturing science and engineering，2005，127（4）:819-828.

［17］秦傲然，蔡安江，戴融.径向剃齿刀设计研究［J］.工具技术，2009，43（1）:70-72.

［18］王沁，贾建军.径向剃齿刀修形的优化设计［J］.工具技术，2014，48（12）:54-56.

［19］SHIH Y P，CHEN S D.A flank correction methodology for a five-axis CNC gear profile grinding machine［J］.Mechanism and Machine Theory，2012，47:31-45.

［20］蒋进科，方宗德，贾海涛.对角修形斜齿轮设计与数控磨齿研究［J］.机械工程学报，2014，50（19）: 158-165.

［21］蒋进科，方宗德，苏进展.高阶传动误差斜齿轮修形设计与加工［J］.哈尔滨工业大学学报，2014，46 （9）:43-49.

［22］蒋进科，方宗德，苏进展.拓扑修形斜齿轮的数控成形磨齿加工［J］.华南理工大学学报:自然科学版，2014，42（4）:97-104.

［23］蒋进科，方宗德，王峰.降低斜齿轮噪声的对角修形优化设计［J］.振动与冲击，2014，33（7）:63-67.

［24］史峰，王辉，郁磊，等.Matlab智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2007:55-60.

（编辑 杨 波）

Grinding plunge shaving cutter for diagonal modified helical gears

JIANG Jinke，FANG Zongde，PENG Xianlong
（School of Mechaincal Engineering，Northwestern Polytechnical University，710072 Xi'an，China）

An approach based on CNC grinding machine of plunge shaving cutter for diagonal modified helical gear was proposed to reduce grinding errors and improve meshing performance.Firstly，the corresponding plunge shaving cutter surfaces for the diagonal modified helical pinion was established based on gear theory.Secondly，a free-form flank topographic correction method based on Y7432 grinding machine，with flat wheel translated along normal sections of invented rack-cutter，was established according to principle of rack-cutter generating involute pinion.Thirdly，an error correction model based on a sensitivity analysis was determined，each axis of the machine was formulated as a six-degree polynomial and a disturbed polynomial coefficient on the topographic flank errors was developed by estimating whether the wheel contacted with the pinion.Finally，using minimum squared error as the objective function to get the smallest grind errors，the PSO optimization algorithm was introduced to solve equations of the corrections，and the polynomial coefficients were ascertained.The result shows that the methods can effectively reduce the grinding error，and the topologically modified tooth for plunge cutter can be represented by sum of longitudinal and diagonal deviations surface.The slight variations in pressure angle and generating angle and helix angle can attain some specific diagonal modified tooth respectively，besides，the diagonal modified helical gear with big size and helix angle can then be efficiently ground by slightly adjusting three-axis movement with a smaller translating flat wheel.

helical gear；diagonal modified；computer numerical control（CNC）grinding；plunge shaving；flat wheel；sensitivity analysis；higher-order correction.

TH133

A

0367-6234（2015）05-0063-08

10.11918/j.issn.0367-6234.2015.05.011

2014-01-10.

国家自然科学基金（51175423，51375384）.

蒋进科（1981—），男，博士研究生；

方宗德（1948—），男，教授，博士生导师.

方宗德，fauto@nwpu.edu.cn.