应用混合粒子群优化的检查点全局优化算法

门朝光，何忠政，陈拥军，李 香，蒋庆丰

（1.哈尔滨工程大学计算机科学与技术学院，150001哈尔滨；2.中国新兴建设开发总公司，100143北京）

应用混合粒子群优化的检查点全局优化算法

门朝光1，何忠政1，陈拥军2，李 香1，蒋庆丰1

（1.哈尔滨工程大学计算机科学与技术学院，150001哈尔滨；2.中国新兴建设开发总公司，100143北京）

针对容错实时系统存在的局部最优检查点间隔为单次故障情况下的最优检查点间隔及局部最优检查点间隔并不是任务集全局最优检查点间隔的缺陷，首先给出检查点间隔全局优化问题的多目标优化模型，然后基于混合粒子群优化算法，提出检查点间隔全局优化算法.该算法通过混合粒子群优化算法的交叉和变异操作，避免算法陷入局部极值的困境，且增强了算法搜索全局近优检查点间隔的能力.实验表明，与其他检查点间隔优化算法相比，本算法可进一步提升系统容错能力.检查点间隔全局优化能在故障多次发生情况下，对任务集的检查点间隔进行全局搜索，以减小检查点设置次数和故障检测次数、高优先级任务抢占时间及故障恢复时间，提高系统可调度性.

实时系统；检查点间隔；容错调度；粒子群优化

在航空航天、军事等多个关键领域已经或正发挥着极其重要作用的实时系统需具备严格的实时性以及高度的可靠性［1］.在实时系统性能提升过程中，电路中晶体管尺寸及工作电压的减小降低了集成电路噪声容限，集成度进一步提高使芯片更易受瞬时故障影响.由瞬时故障所导致的计算机可靠性已成为一个严峻的课题［2-3］.瞬时故障影响设备的性能及其中任务的可靠、有效及正确执行，因此瞬时故障容错技术对系统的实时性及可靠性保证至关重要.

可调度性分析能够确保系统实时性及可靠性［4］.若任务集所有任务的最坏响应时间都不超过各自的截止时间，则该任务集是可调度的.基于检查点设置和卷回恢复技术进行任务的容错调度，能在瞬时故障多次发生情况下，将任务恢复至过去某一正确状态，把计算损失减小为检查点建立时刻至故障发生时刻所做的计算.局部最优检查点间隔能在提供容错能力的同时，最小化任务额外执行时间.检查点间隔全局优化通过增加或减小任务的检查点数量，使不能满足截止时间要求的任务可以抢占其他任务的空闲时间.

实时系统容错调度算法已经进行了大量的研究.文献［5］提出卷回恢复模型下实时系统任务最坏响应时间计算公式，但该文的检查点间隔是单次故障情况下的局部最优检查点间隔.文献［6］分析实时系统中多次故障发生时进程的可调度性.该文中模型的故障发生次数是确定的，而故障次数是由任务响应时间和故障发生间隔决定的.文献［7］提出拥有不同截止时间的多任务最优检查点间隔算法，但该算法仅适用于拥有谐波周期的多个任务.

粒子群优化（PSO）算法是一种源于对鸟群捕食行为的研究而发明的进化计算技术［8］.该算法具有较强的局部搜索能力和很好的全局寻优能力.PSO算法等一些进化优化算法已被用于求解多目标优化问题［9］.

1 任务容错调度模型

实时系统调度的任务集合为Γ=｛τ1，τ2，…，τn｝，其中:τi为实时周期性任务.在卷回恢复容错模型下，任务τi可表示为七元组＜Ti，Di，Ci，ni，Oi，αi，μi＞，其中Ti、Di、Ci分别为τi的周期、截止时间、执行时间，且三者满足Ci＜Di≤Ti；ni为τi的检查点数量，任务开始执行时设置第1个检查点，任务结束时不设置检查点；Oi为τi设置一个检查点的开销；αi为故障检测开销；μi为卷回恢复开销.

系统对任务集Γ进行实时调度时，首先需采用优先级调度算法（如速率单调算法（RM）［10］或时限单调算法（DM）［11］）为任务集Γ中的每个任务τi分配固定且唯一的优先级pi（pi∈｛1，2，…，n｝）.τi的优先级越高，其对应的pi越大.根据任务τi的优先级pi可定义任务集Γ的两个任务子集.

1）优先级高于pi的任务所组成的集合hp（i）为

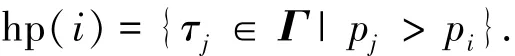
2）优先级不低于 pi的任务所组成的集合hpe（i）为

本文基于的条件为:仅考虑瞬时故障的容错处理，且瞬时故障能在故障检测阶段被成功检测，没有错误传递；所有任务之间均相互独立，没有资源共享引起的任务阻塞；采用等间隔检查点设置.两个连续发生的故障之间存在最小时间间隔TE，TE越小，表明系统容错能力越强，因此可用TE来衡量系统容错能力［12］.

文献［5］中的任务最坏响应时间忽略故障恢复开销；而检查点设置及故障的检测、恢复是实现容错必需的过程，且对于不同的任务三者的时间开销各不相同，即使相同任务在不同的时间和负载时，三者的时间开销也不同.检查点卷回恢复的开销由检查点间隔决定，检查点设置和故障检测的次数也由检查点间隔决定，因此检查点间隔对容错实时系统任务的可调度性有重要影响.不同配置的任务在相同的TE下，其故障发生次数不同，任务的局部最优检查点间隔不同.相同的任务在不同的TE下，故障发生次数也不同，因此局部最优检查点间隔也不同.且对于拥有多个任务的任务集而言，任务的全局最优检查点间隔与局部最优检查点间隔也不一定相同.在特定TE下，最坏响应时间Ri（ni）可表示为检查点数量ni的函数.

图1是文献［6］提出的基于检查点设置和卷回恢复技术的容错模型，该模型中任务τ1的检查点数量为6且故障发生次数为2次.故障发生在τ1的第3个和第6个检查点间隔.基于该模型，在任务可能发生多次故障的情况下，同时考虑检查点设置开销、故障检测开销、故障恢复开销，得任务最坏响应时间计算公式Ri（ni）为

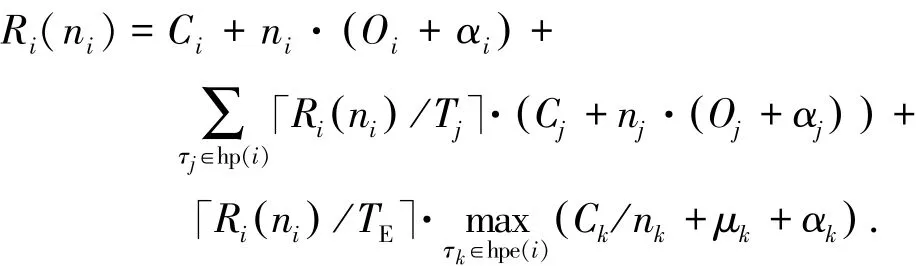
式中Ri（ni）为τi的执行时间、检查点设置时间和故障检测时间、高优先级任务的抢占时间及故障恢复时间之和.故障恢复时间是在任务的最坏响应时间内任务故障发生次数和最大故障恢复开销的乘积.故障恢复时间包含相应的检查点间隔执行时间（Ck/nk）、卷回恢复开销和故障检测开销.

图1 基于检查点设置和卷回恢复技术的容错模型

2 检查点间隔全局优化问题

局部最优检查点间隔是任务单独执行时的最优检查点间隔.具有优先级关系的多个任务并发执行时，高优先级的任务会抢占低优先级任务的执行，因此每个任务发生故障的次数较单独执行时有所变化.如图2所示，在τi执行过程中，由于高优先级任务τj的周期性抢占，使τi的响应时间由73变为80，其故障发生次数较τi单独执行时的次数（「73/15⌉=5）增加.如图3所示，在τi执行过程中，由于高优先级任务τj的抢占，使τi的响应时间由18变为55，其故障发生次数较τi单独执行时的次数（「18/15⌉=2）减少.因此单任务局部最优检查点间隔并不是任务集全局最优检查点间隔.

图2 故障次数增加的情况

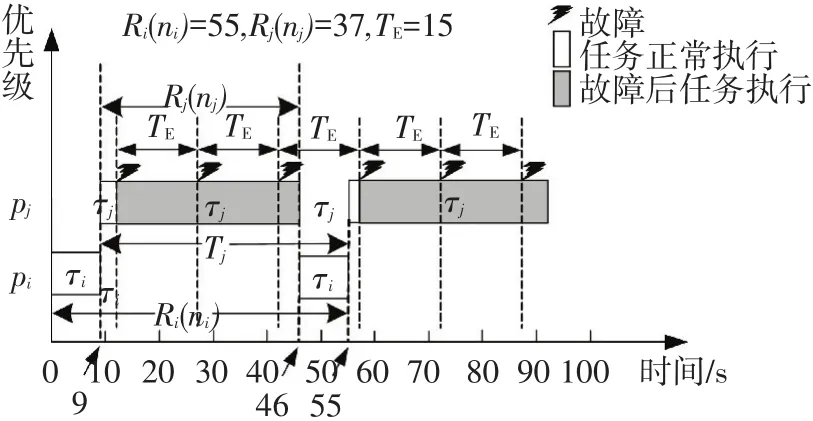
图3 故障次数减少的情况

在检查点间隔全局优化时，如果为了减小不可调度任务的最坏响应时间中的故障恢复时间，而增加引起最大故障恢复时间任务τi的检查点数量，那么τi的检查点设置和故障检测次数将会增加，由这两部分所引起的时间开销也会增加.而且对于其他的低优先级任务τj（τi∈hp（τj）），其高优先级任务的抢占执行时间将会增加，这可能导致τj不能满足其截止时间要求.如果为了减小不可调度任务的最坏响应时间中的高优先级任务抢占执行时间，而减小非最大故障恢复时间开销任务τi的检查点数量，那么τi的检查点设置和故障检测次数将会减小，由这两部分所引起的时间开销也会减小.对于τi自身及其他低优先级任务τj（τi∈hp（τj）），其故障恢复时间可能会增加，这可能导致τi和τj不能满足其截止时间要求.每个任务在优化其自身的检查点间隔时，有可能导致其他任务的最坏响应时间增加.因此通过检查点间隔优化来最小化各个任务的Ri（ni）是相互冲突的.检查点间隔全局优化问题的数学形式可描述为如下的多目标优化问题:

式中N为由元素n1，n2，…，nn构成的向量.任务τi检查点数量ni的取值范围首先要确保检查点技术能够有效的执行，即在检查点间隔执行时间、检查点设置开销和故障检测开销之和与检查点间隔执行时间、故障检测开销和卷回恢复开销之和两者的最大值内只能发生一次故障；而且检查点数量取值范围还要确保检查点间隔执行时间大于检查点设置开销、故障检测开销与卷回恢复开销三者的最大值.

3 检查点间隔全局优化算法

PSO算法中每个粒子i包含两个D维的向量:位置向量xi=（xi1，xi2，…，xiD）和速度向量vi=（vi1，vi2，…，viD）.在PSO算法搜索解空间时，粒子i需要保存其搜索到的自身最优位置pbi=（pbi1，pbi2，…，pbiD），种群需要保存当前群体全局最优位置gbg= （gbg1，gbg2，…，gbgD）.在PSO算法迭代计算时，粒子速度向量中的每维元素根据自身惯性大小（即当前速度大小）和粒子自身最优位置中该元素对应的最优位置及群体全局最优位置中该元素对应的最优位置来动态调整自身的速度，以改善该元素的位置.粒子i第d维元素的第t+1次迭代进化的速度计算公式和位置计算公式分别为

式中:ω为惯性权重因子；c1、c2分别为加速因子，其取值为正常数；r1、r2分别为区间［0，1］中均匀分布的随机数；d为D维粒子中的维数，d∈｛1，2，…，D｝；pb为第t次迭代进化时粒子xi中第d维元素的自身最优位置；为第t次迭代进化时第d维元素的群体最优位置.

3.1 编码

本算法中离散编码方式的编码长度等于任务个数，粒子中每个元素的位置表示对应任务的检查点数量.粒子xi的编码方案为xi=（xi1，xi2，…，xiD）.其中，xij为任务集Γ中任务 τj的检查点数量，粒子的维数D为任务集中任务的数量n.

种群初始化时根据ChekptLN算法［13］求解每个任务的局部最优检查点间隔，然后在每个任务的局部最优检查点间隔附近随机生成初始解，随机生成满足约束条件的初始速度向量vi=（vi1，vi2，…，viD）.

3.2 适应度函数

本算法的目的是使所有任务在满足截止时间要求的前提下最小化最坏响应时间.因此粒子xi的适应度函数Fit（xi）可定义为

可以看出，适应度函数为粒子所代表的所有任务的截止时间与最坏响应时间差值中的最小值.如果粒子xi的最小差值越大，那么Fit（xi）的函数值越大，该粒子的位置就越有可能成为种群全局最优位置.

3.3 交叉

PSO算法的粒子速度和位置更新方法使得粒子可能会受某个局部最优值影响而陷入局部极小点.遗传算法能够使得粒子摆脱这种困境的干扰.因此能够借鉴遗传算法的交叉和变异进化机制对PSO算法进行改进的混合PSO算法［14］被提出.

混合PSO算法按照交叉概率μc对选取的粒子进行交叉操作.交叉运算将粒子中的所有元素进行交叉操作，对于粒子xi和xj中的元素xid和xjd及其对应的速度vid和vjd交叉操作方式为

3.4 变异

混合PSO算法按照变异概率μm，对粒子中随机选取的第d维元素进行变异.变异可增大或减小检查点数量.位置和速度的变异方式分别为

3.5 基于混合PSO的检查点间隔全局优化算法

基于混合PSO算法的检查点间隔全局优化算法具体步骤如图4所示.

图4 混合PSO的检查点间隔全局优化算法具体步骤

如果忽略算法的任务最坏响应时间计算开销，在交叉操作和变异操作同时进行的情况下，算法在某一特定的故障发生间隔求解全局优化检查点间隔时的复杂度为O（I×n×（cm2+M）），即算法的内层while循环的复杂度.其中:I为群体进化次数；n为任务集中任务数量；cm为交叉操作粒子数目；M为群体规模.

4 性能评估

为验证检查点间隔全局优化算法的高效性，本文用仿真试验模拟810个任务集，每个任务集包含6个实时周期性任务（可扩展至包含任意数量任务的任务集）.试验计算机配置为:Intel（R）E4500 CPU，2 G内存，500 G硬盘.参照文献［13］中方法，随机产生Γ中各任务的配置属性，但任务τi的配置须满足以下条件:

1）τi的周期 Ti和截止时间 Di均为区间［100，4 000］上的均匀分布，而且Di≤Ti；

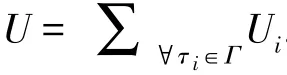
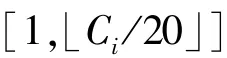
4）混合PSO算法配置为:M为区间［20，100］上的随机数，I为区间［20，60］上的随机数，cm为区间［10，40］上的随机数且小于M，c1和c2都为2，r1和r2为区间［0，1］上的随机数，μc和μm分别为0.8和0.4.ω采用线性递减权值策略求解，如

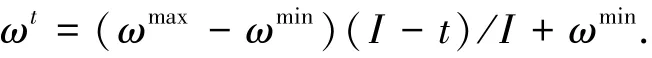
式中:ωmax、ωmin分别为惯性权重的最大值和最小值，典型取值为ωmax=0.9，ωmin=0.4；ωt为当前惯性权重值；t为种群当前进化次数.

采用优先级调度算法RM对任务集Γ进行容错实时调度.在同时考虑故障检测、故障恢复和检查点设置开销情况下，计算Γ分别在文献［5］中基于单次故障优化检查点间隔算法、ChekptLN算法［13］、CIGO算法［13］和本文算法下所能达到的最小故障发生间隔STE、LTE、GTGE和GTE.与文献［5］算法相比，本文算法的系统容错能力提升程度通过式（7）来衡量.

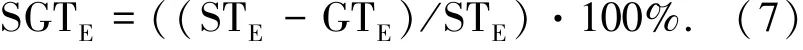
与ChekptLN算法相比，本文算法的系统容错能力提升程度通过式（8）来衡量.

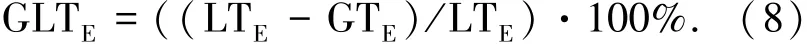
与CIGO算法相比，本文算法的系统容错能力提升程度通过式（9）来衡量.

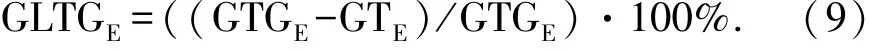
本文算法相对于文献［5］算法、ChekptLN算法、CIGO算法系统容错能力提升情况分别如图5～图7所示.图5～图7中纵坐标分别表示系统容错能力的提升程度SGTE、GLTE和GLTGE，横坐标都表示处理器利用率U，黑点分别表示一个任务集对应的SGTE、GLTE和GLTGE.

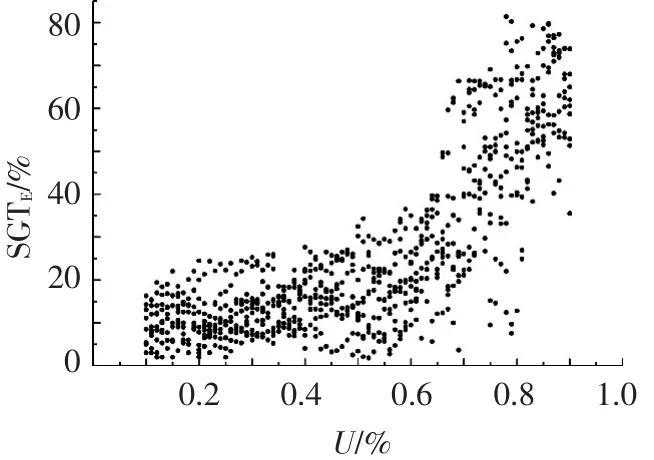
图5 本文算法相对于文献［5］中算法容错能力提升情况

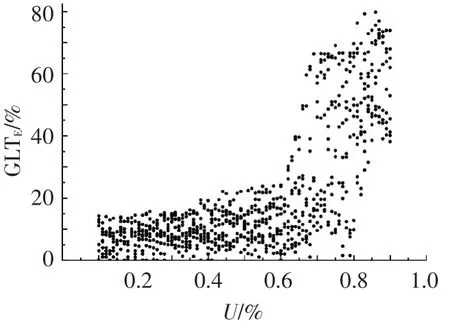
图6 本文算法相对于ChekptLN算法容错能力提升情况

图7 本文算法相对于CIGO算法容错能力提升情况

由图5可知，与文献［5］中算法的容错能力相比，本文算法能够大幅提升系统容错能力.当0.1≤U＜0.5时，SGTE较小，但容错能力提升幅度也较明显.当0.5≤U≤0.9时，SGTE变化区域范围较大.因为此时任务检查点间隔为发生一次故障时的优化检查点间隔，此时任务的最坏响应时间较大.任务在实际执行时发生多次故障是极有可能的；在不同的TE时，故障发生次数不同，任务的最优检查点间隔也不同.对于拥有多个任务的任务集而言，全局最优检查点间隔为当前TE时任务集中所有任务的最优检查点间隔.本文算法中的检查点间隔全局优化能减少任务的检查点设置和故障检测次数、减小故障恢复时间、减小抢占任务的执行时间来减小任务最坏响应时间，使任务满足其截止时间要求，从而大幅降低TE.由实验结果知SGTE为零的情况极少，说明基于单次故障优化检查点间隔算法的容错能力存在较大提升空间.

由图6可知，当0.1≤U＜0.6时，GLTE较小且基本不超过25%；当0.6≤U≤0.9时，GLTE在较大区域内变化.容错能力提升程度呈现该分布规律的原因在于:当U较低时，任务可以利用自身的空闲时间来进行卷回恢复以实现瞬时故障容错，此时TE可能已接近其下限，检查点间隔全局优化对TE的提升空间较小.当U较高时，在局部最优检查点间隔时任务自身空闲时间不足以完成瞬时故障容错，所以此时TE较大.本文算法能够对任务集中所有任务的检查点间隔进行全局优化，以减少任务的检查点设置和故障检测次数或者减小抢占任务执行时间、故障恢复时间来满足任务的截止时间要求，从而大幅降低TE.GLTE有时可能为零，此时检查点间隔全局优化不能提升系统的容错能力.这主要是由于检查点数量的改变已经不能改善任务的最坏响应时间或者不存在满足优化约束条件的任务.

由图7可知，本文算法的系统容错能力优于CIGO算法.这得益于混合PSO算法的全局优化能力.由于CIGO算法在检查点间隔全局优化时，并没有全局考虑，仅仅是首先增加最大故障恢复开销任务的检查点数量，这样最大故障恢复开销任务集合和非最大故障恢复开销任务集合已经改变，在后续优化中检查点数量减小任务集合的定义已经并不准确，所以影响其全局优化能力.在U较小时，本文算法系统容错能力的优势与CIGO算法相比并不是太大，多数情况下不能进一步提高系统的容错能力；但是在U较大时，本文算法系统容错能力较CIGO算法的优势比较明显，但是由于此时两种算法所能达到的最小故障发生间隔较大，所以由式（9）计算的值较小.

5 结 语

针对实时系统卷回恢复容错模型局部最优检查点间隔并不是任务多次故障下的最优检查点间隔及局部最优检查点间隔并不是任务集全局最优检查点间隔的缺陷，本文对实时系统的容错调度进行研究，基于混合PSO算法所具有的遗传算法和PSO算法的优点，提出任务检查点间隔全局优化算法.该算法通过遗传算法的交叉和变异操作来增强PSO算法的全局寻优能力，对任务集检查点间隔进行全局优化.由仿真实验可知，检查点间隔全局优化算法能够在基于单次故障优化检查点间隔的算法和局部最优检查点间隔算法的基础上进一步提升系统的容错能力，且该算法的系统容错能力优于CIGO算法.

［1］SHA L，ABDELZAHER T F，ARAEN K E，et al.Real time scheduling theory:a historical perspective［J］.Real-Time Systems，2004，28（2/3）:101-155.

［2］傅忠传，陈红松，崔刚，等.处理器容错技术研究与展望［J］.计算机研究与发展，2007，44（1）:154-160.

［3］CLARK J A，PRADHAN D K.Fault injection:a method for validating computer system dependability［J］.IEEE Computer，1995，28（6）:47-56.

［4］ZHANG F，BURNS A.Schedulability analysis for realtime systems with EDF scheduling［J］.IEEE Transactions on Computers，2009，58（9）:1250-1258.

［5］PUNNEKKAT S，BURNS A，DAVIS R.Analysis of checkpointing forreal-timesystems［J］.Real-Time Systems，2001，20（1）:83-102.

［6］POP P，IZOSIMOV V， ELES P， etal.Design optimization of time and cost-constrained fault-tolerant embedded systems with checkpointing and replication［J］.IEEE Transactions on VeryLargeScaleIntegration Systems，2009，17（3）:389-402

［7］KWAK S W，YANG J M.Optimal checkpoint placement on real-time tasks with harmonic periods［J］.Journal of Computer Science and Technology，2012，27（1）:105-112.

［8］KENNEDY J， EBERHART R.Particle swarm optimization［C］//Proceedings of IEEE International Conference on Neural Networks.Perth:IEEE，1995: 1942-1948.

［9］公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究［J］.软件学报，2009，20（2）:271-289.

［10］LIU L C，LAYLAND J W.Scheduling algorithms for multi-programming in a hard real-time environment［J］.Journal of the ACM，1973，20（1）:46-61.

［11］AUDSLEY N C，BURNS A，WELLINGS A J.Deadline monotonic scheduling theory and application［J］.Control Engineering Practice，1993，1（1）:71-78.

［12］BURNS A，PUNNEKKAT S，STRINGINI L，et al.Probabilistic scheduling guarantees for fault-tolerant realtime systems［C］ //ProceedingsofInternational WorkingConference on Dependable Computing for Critical Applications.San Jose:IEEE，1999:361-378.

［13］何忠政，门朝光，李香.基于检查点间隔优化的容错实时系统可调度性［J］.吉林大学学报:工学版，2014，44（2）:433-439.

［14］时小虎，韩世迁，闵克学，等.基于遗传算法和粒子群优化的混合算法［EB/OL］.北京:中国科技论文在线，［2006-10-27］.http://www.paper.edu.cn/ releasepaper/content/200610-461.

（编辑 张 红）

The checkpoint global optimization algorithm based on the mixed particle swarm optimization

MEN Chaoguang1，HE Zhongzheng1，CHEN Yongjun2，LI Xiang1，JIANG Qingfeng1
（1.College of Computer Science and Technology，Harbin Engineering University，150001 Harbin，China；2.China Xinxing Construction&Development General Company，100143 Beijing，China）

For the task sets in the fault tolerant real time systems，the disadvantages of the local optimal checkpoint interval are under a single fault assumption and also not the global optimal checkpoint interval.To solve these，the multi-objective optimization model for the checkpoint interval global optimization was given first，and then the checkpoint interval global optimization algorithm based on the mixed particle swarm optimization algorithm was proposed.This algorithm avoids the shortcoming of falling into local optimum and enhances the ability of searching the global approximate optimal checkpoint interval by the crossover and mutation operations of the mixed particle swarm optimization algorithm，and further reduces the task worst case response time.The simulation results show that the algorithm can further improve the system fault resilience over the other checkpoint interval optimization algorithms.At the same time，the checkpoint interval global optimization can search the checkpoint intervals of the task set globally when the faults occur many times，by which the number of checkpoint and the number of fault detection can be reduced and the preemption time by the high priority tasks and the fault recovery time can also be decreased，and also the system schedulability can be improved.

real-time systems；checkpoint interval；fault tolerant scheduling；particle swarm optimization

TP316

A

0367-6234（2015）05-0091-06

10.11918/j.issn.0367-6234.2015.05.016

2014-04-20.

国家自然科学基金（60873138，61100004）.

门朝光（1963—），男，教授，博士生导师.

门朝光，menchaoguang@hrbeu.edu.cn.