充气伸长型气动柔性驱动器刚度特性

滕 燕，高 帅

（南京理工大学机械工程学院，210094南京）

充气伸长型气动柔性驱动器刚度特性

滕 燕，高 帅

（南京理工大学机械工程学院，210094南京）

为实现充气伸长型气动柔性驱动器的变刚度控制，对其输出力模型进行改进，建立气动柔性驱动器的静态刚度和动态刚度数学模型，指出气动柔性驱动器的动态刚度为静态刚度与气压刚度之和.试验和仿真研究结果表明:供气压力是影响充气伸长型气动柔性驱动器静态刚度和动态刚度的主要因素，静态刚度和动态刚度均随供气压力的增大而增大，且呈现较好的线性关系.

气动柔性驱动器；静态刚度；动态刚度；气压刚度；供气压力

气动柔性驱动器又称气动人工肌肉，是近年来发展起来的一种柔顺性好、安全性高的气动驱动元件，在医疗康复领域具有广阔的应用前景［1-2］.近年来，利用传统的Mckibben型气动人工肌肉已开发了一些柔顺关节康复训练器械［3-4］，为了实现对其变刚度控制，很多学者对Mckibben型气动人工肌肉的工作特性和刚度进行了研究［5-10］.但由于Mckibben型气动人工肌肉的行程较短，而且所构成的关节康复器的转动驱动结构也比较复杂，一定程度上限制了这一类柔顺关节康复器的推广应用.文献［11-12］研发了气动柔性驱动器，其驱动主体均为一个嵌入了螺旋弹簧的橡胶管，充气后橡胶管膨胀，拉伸弹簧产生轴向位移；但受弹簧和橡胶材料的限制，这种气动柔性驱动器的轴向输出位移较小，驱动力也较小.文献［13-14］提出了一种由扁平橡胶管螺旋卷绕构成的气动驱动器WTA，当向橡胶管内充气后，螺旋管膨胀，气动驱动器产生转矩，推动关节旋转，但输出的转矩较小.文献［15］提出了一种褶皱式气动肌肉，并对其刚度特性进行了研究，与Mckibben型气动人工肌肉相比，褶皱式气动肌肉具有输出力和收缩率大的特点，但其仍为充气收缩型的气动肌肉，在构成关节康复器械时结构仍比较复杂［16］.笔者所在的技术中心研发了一种充气伸长型气动柔性驱动器［17］，它由初始截面为扁平状的弹性橡胶管以及套在橡胶管外的纤维编织网经螺旋缠绕构成，与传统的Mckibben型气动人工肌肉相比，具有行程长、推力大的特点，在构成关节康复训练器驱动部件时结构更简单；与WTA相比，具有输出位移直线度和可控性更好等特点.笔者在前期基于这种充气伸长型气动柔性驱动器，开发了具有柔顺性和主-被动训练功能的柔顺膝关节康复训练装置［18］.

本文在前期研究工作［19］的基础上，对充气伸长型气动柔性驱动器的输出力模型进行改进，研究探讨该柔性驱动器的刚度特性，建立静态刚度和动态刚度数学模型，并进行试验研究.

1 充气伸长型气动柔性驱动器输出力改进模型

图1为充气伸长型气动柔性驱动器的工作示意，图2为该气动柔性驱动器弹性橡胶管螺旋缠绕一层的断面几何尺寸示意.其中H为气动柔性驱动器的工作长度，R为螺旋弹性橡胶管膨胀至圆形时的外圈半径，D为中心导向杆直径.当向螺旋缠绕的扁平弹性橡胶管中充入压缩空气时，橡胶管膨胀并沿轴向产生变形，对外输出力和位移.

图1 气动柔性驱动器充气变形工作示意

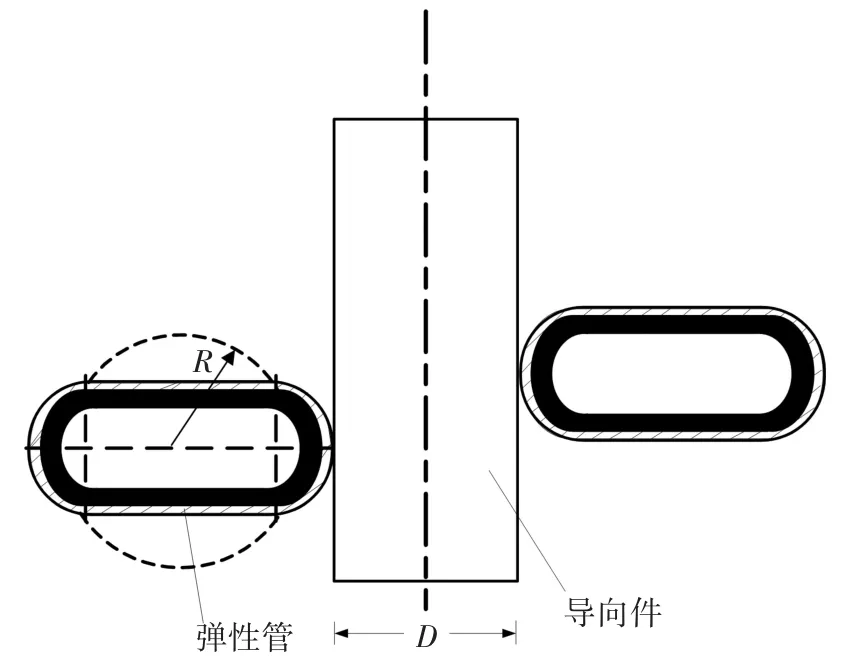
图2 气动柔性驱动器几何尺寸示意

笔者前期对该气动柔性驱动器的输出力数学模型进行了研究［19］，为了方便，推导过程中忽略了气动柔性驱动器充气伸长时弹性橡胶管的弹性力以及纤维编织网与弹性橡胶管之间的摩擦力.但试验研究发现，由于这两点因素的存在，气动柔性驱动器实际上无法伸长到理论的最大长度，因此该模型存在较大的误差.为此，本文对该气动柔性驱动器的输出力模型进行改进研究.

引入气动柔性驱动器伸长长度校正系数Kp，并定义Kp为充气伸长型气动柔性驱动器理论伸长的最大长度Hmax与实际伸长的最大长度Hp之比，即Kp=Hmax/Hp.通过试验测量不同供气压力p下充气伸长型气动柔性驱动器的实际伸长最大长度，可以计算得到校正系数Kp.表1给出了几种供气压力下Kp的取值.

表1 不同供气压力下气动柔性驱动器伸长长度校正系数Kp

利用校正系数Kp对充气伸长型气动柔性驱动器的输出力模型进行改进，得到的改进模型为

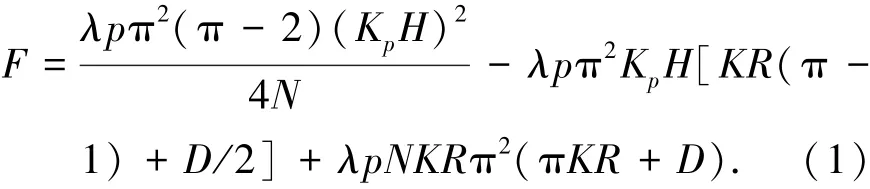
式中:F为驱动器输出力，N；λ为气动柔性驱动器的能量转化效率（由试验确定）；p为供气压力，MPa；H为柔性驱动器的工作长度，mm；N为弹性管的层数；R为螺旋管膨胀至圆形时的外圈半径，mm；K为螺旋管的半径变化率；D为导向杆直径，mm.

2 充气伸长型气动柔性驱动器的刚度

2.1 静态刚度模型

当供气压力一定时，气动柔性驱动器的静态刚度可以表示为

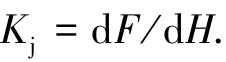
根据式（1）可得静态刚度的表达式为

2.2 动态刚度模型

定义气动柔性驱动器的动态刚度为气动柔性驱动器充气伸长过程中所具有的刚度.令

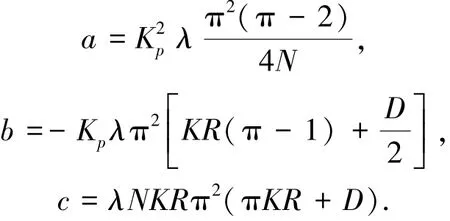
则根据式（2）有

考虑到气动柔性驱动器的类弹簧特征［5-8］，充气伸长过程中的输出力可表示为

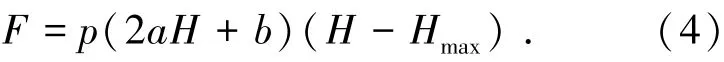
对式（4）进行求导，可得动态刚度为

可以推导出

比较式（5）和式（3）可以看出，气动柔性驱动器的动态刚度包含静态刚度以及由于工作过程中受外负载作用引起的气动柔性驱动器长度变化和气腔内气压变化引起的附加刚度，定义这种附加刚度为气压刚度Kq，即

式（6）又可以写为

式中A为气动柔性驱动器的等效截面积，mm2.

假设气动柔性驱动器的充气过程为绝热过程，则有

式中:n为绝热指数，n=1.4；V=AH.

对式（8）求导得

根据文献［19］和式（4），有

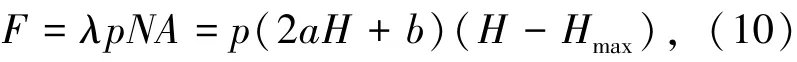
可得

联立式（7）～（11），可得气压刚度为

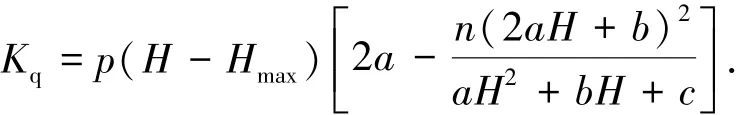
综上，充气伸长型气动柔性驱动器的动态刚度为

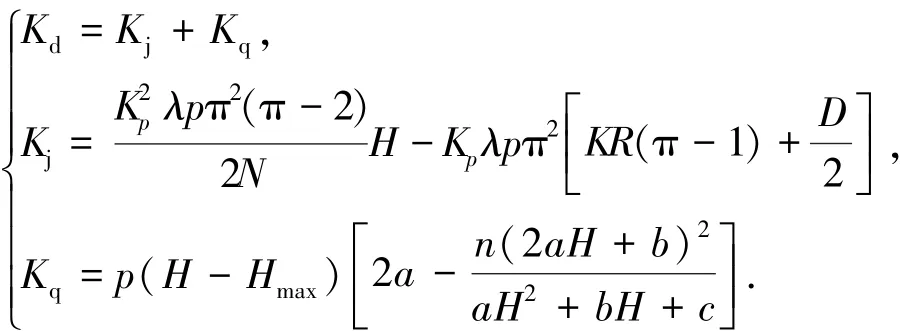
3 充气伸长型气动柔性驱动器刚度特性试验

图3为试验平台的主要组成.气动柔性驱动器的结构参数为:自由状态下的长度H为70 mm，弹性管层数N为12，螺旋弹性橡胶管膨胀至圆形时的外圈半径R为5 mm，导向杆直径D为25 mm.试验中，通过长度调节环调节气动柔性驱动器的工作长度，从70 mm开始，按每次2.5 mm递增，直至达到相应供气压力下的最大工作长度.每种工作长度下，改变供气压力从 0—0.3—0 MPa，按0.05 MPa递增或递减.测试气动柔性驱动器在不同工作长度、不同供气压力下的输出力变化曲线.

图3 试验平台的主要组成

3.1 气动柔性驱动器的等压特性

充气伸长型气动柔性驱动器的等压特性试验结果如图4所示.与前期的研究结果［19］进行比较发现:不同供气压力下气动柔性驱动器的最大工作长度并不相同，由改进模型计算得到的气动柔性驱动器的输出力值与实际测试得到的试验值的吻合程度更高.本次试验条件下，供气压力为0.30 MPa时，气动柔性驱动器的最大工作伸长长度可达122.5 mm，最大输出力约为225 N.

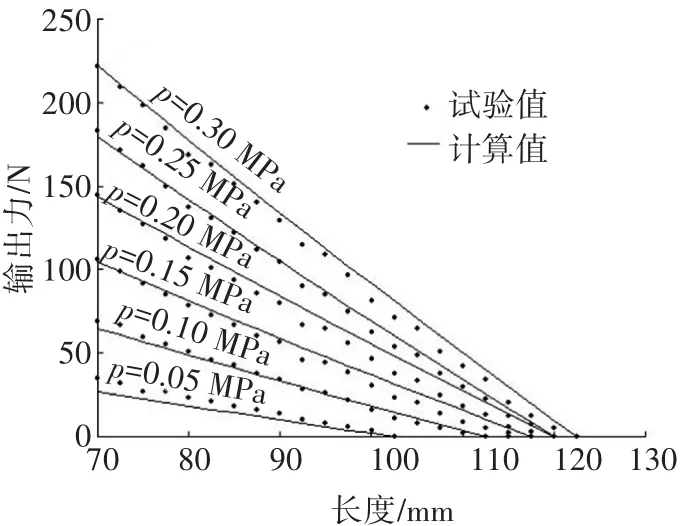
图4 气动柔性驱动器的等压特性

3.2 气动柔性驱动器的静态刚度

充气伸长型气动柔性驱动器的静态刚度试验结果如图5所示.可以看出:在同一供气压力条件下，充气伸长型气动柔性驱动器的静态刚度随工作长度的增大而减小，但减小幅度不大；在同一工作长度条件下，以工作长度90 mm为例，气动柔性驱动器的静态刚度随供气压力的增大而增大，且表现出较好的线性关系.在本次试验条件下，供气压力为0.3 MPa时，气动柔性驱动器的静态刚度最大约为5 000 N/m.

图5 气动柔性驱动器的静态刚度

3.3 气动柔性驱动器的动态刚度

图6给出了充气伸长型气动柔性驱动器气压刚度的理论计算结果，可以看出:气压刚度随着工作长度的增加逐渐减小，最终变为零，相对于静态刚度，气压刚度要小得多.供气压力为0.05 MPa时的最大气压刚度约80 N/m，为静态刚度的1/10左右；供气压力为0.3 MPa时的最大气压刚度约700 N/m，为静态刚度的1/7左右，说明当供气压力增大，气压刚度对动态刚度的影响程度也将增大.

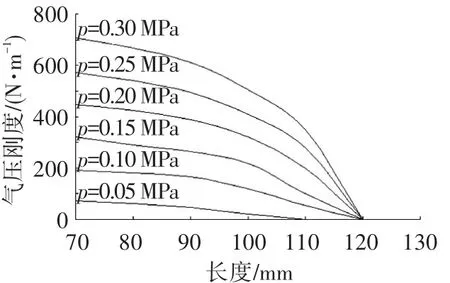
图6 气动柔性驱动器的气压刚度

充气伸长型气动柔性驱动器的动态刚度试验结果如图7所示.可以看出:在同一供气压力下，气动柔性驱动器的动态刚度随工作长度的增大而减小，但减小幅度不大；在同一工作长度下，以工作长度90 mm为例，气动柔性驱动器的动态刚度随着供气压力的增大而增大，且表现出较好的线性关系.

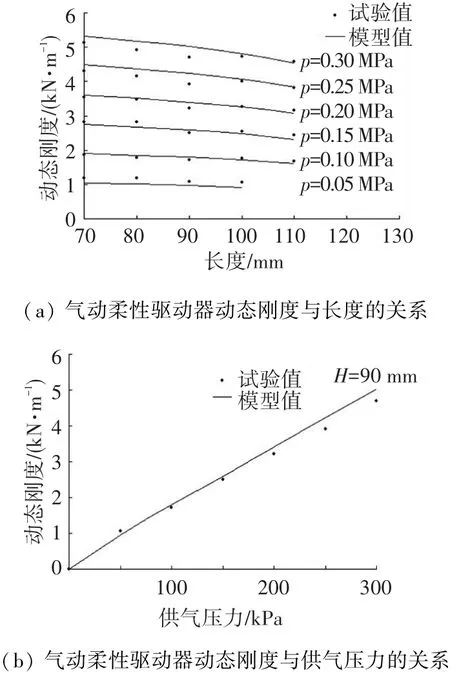
图7 气动柔性驱动器的动态刚度

综上可知，供气压力是影响气动柔性驱动器静态刚度和动态刚度的主要因素，且静态刚度和动态刚度均与供气压力呈现较好的线性关系.比较图5和7发现:气动柔性驱动器的动态刚度和静态刚度试验值的差值（即气压刚度）很小，远远小于理论计算值.这是由于在试验中，气动柔性驱动器的供气流量调节得较小，使得充气过程较长，充气过程不再是绝热过程，由气压快速变化导致的气压刚度较小.

4 结 论

1）通过引入伸长长度校正系数Kp，建立了充气伸长型气动柔性驱动器的输出力改进模型，由改进模型计算得到的充气伸长型气动柔性驱动器输出力与试验值有较好的一致性，说明改进模型能准确地反映气动柔性驱动器的实际输出力；

2）推导了充气伸长型气动柔性驱动器的静态刚度和动态刚度理论模型，动态刚度为静态刚度与气压刚度之和.静态刚度、气压刚度和动态刚度均表现出随供气压力的增大而增大、随工作长度的增大而减小的变化趋势.但气压刚度远小于静态刚度.

3）供气压力对气动柔性驱动器静态刚度和动态刚度的影响程度要远远超过工作长度的影响程度，供气压力为影响气动柔性驱动器刚度的主要因素，且供气压力与静态刚度、动态刚度均表现出较好的线性关系.该结论为气动柔性驱动器的变刚度控制奠定了理论基础.

［1］KRISHNA S，NAGARAJAN T，RANI A M A.Review of current development of pneumatic artificial muscle ［J］.Journal of Applied Sciences，2011，11（10）: 1749-1755.

［2］陶国良，谢建蔚，周洪.气动人工肌肉的发展趋势与研究现状［J］.机械工程学报，2009，45（10）:75-83.

［3］SAWICKI G S，GORDON K E，FERRIS D P.Powered lower limb orthoses:applications in motor adaptation and rehabilitation［C］//9th International Conference on Rehabilitation Robotics.Piscataway:IEEE Computer Society，2005:206-211.

［4］RUPP R，PLEWA H，HOFER E P，et al.Motion Therapy@ Home-a robotic device for automated locomotion therapy at home［C］//IEEE 11th International Conference on Rehabilitation Robotics.Piscataway:IEEE Computer Society，2009:395-400.

［5］隋立明，王祖温，包钢.气动肌肉的刚度特性分析［J］.中国机械工程，2004，15（3）:242-244.

［6］傅晓云，方敏，李宝仁.气动人工肌肉刚度特性的分析［J］.机床与液压，2007，35（2）:109-111.

［7］刘吉轩，苏俊收.气动肌肉驱动器的动态刚度和阻尼特性［J］.流体传动与控制，2011（1）:13-17.

［8］TÓTHOVÁ M，HOŠOVSKý A.Dynamic simulation model of pneumatic actuator with artificial muscle［C］// IEEE 11th International Symposium on Applied Machine Intelligence and Informatics.Washington DC:IEEE Computer Society，2013:47-51.

［9］ TÓTHOVÁ M， PITEL′J.Simulation of actuator dynamicsbased on geometricmodelofpneumatic artificial muscle ［C］//IEEE 11th International Symposium on IntelligentSystem and Informatics.Washington DC:IEEE Computer Society，2013:233-237.

［10］WICKRAMATUNGE K C，LEEPHAKPREEDA T.Study on mechanical behaviors of pneumatic artificial muscle［J］.InternationalJournalofEngineering Science，2010，48（2）:188-198.

［11］张立彬，杨庆华，鲍官军，等.一种气动柔性驱动器:中国，200510049589.5［P］.2005-09-21［2014-05-05］.http://www.soopat.com/Patent/200510049589.

［12］张贵兰，耿德旭，刘晓敏，等.伸长型气动人工肌肉轴向力学特性分析［J］.机械工程师，2010（12）: 7-8.

［13］TSUKAGOSHI H，KITAGAWA A，KAMATA Y.Wearable fluid power composed of transformed flat tube actuators ［C］//Proceedings of the 2002 IEEE/RSJ Int Conference on Intelligent Robots and Systems EPFL.Lausanne:IEEE，2002:1178-1183.

［14］北川能，塚越秀行.螺旋チュープアクチュエータ:日本，P2001-107178［P］.2002-10-18.［2014-05-05］.http://www.j-tokkyo.com/2002/F15B/JP2002-303303.shtml.

［15］DAERDEN F，LEFEBER D，VERRELST B，et al.Pleated pneumatic artificial muscles:compliant robotic actuators［C］//Proceedings of the 2001 IEEE/RSJ InternationalConference on IntelligentRobots and Systems.Maui:IEEE，2001:1958-1963.

［16］VANDERBORGHT B，VERRELST B，VAN HAM R，et al.Torque and compliance control of the pneumatic artificialmuscles in the biped “Lucy”［C］// Proceedings of the 2006 IEEE International Conference on Robotics and Automation.Orlando:IEEE，2006: 842-847.

［17］李小宁，滕燕，杨罡，等.充气伸长型气动柔性驱动器:中国，201010146317.8［P］.2010-10-20［2014-05-05］.http://www.soopat.com/Patent/201010146317.

［18］李小宁，滕燕，杨罡，等.双向柔性的膝关节主-被动康复训练装置:中国，201010146310.6［P］.2010-09-15［2014-05-05］.http://www.soopat.com/ Patent/201010146310？lx=FMSQ.

［19］滕燕，杨罡，李小宁，等.推力大行程气动柔性驱动器及其特性［J］.南京理工大学学报，2011，35（4）: 502-506.

（编辑 杨 波）

Stiffness characteristic of elongation type pneumatic compliance actuator

TENG Yan，GAO Shuai
（School of Mechanical Engineering，Nanjing University of Science and Technology，210094 Nanjing，China）

The output force model of elongation type pneumatic compliance actuator has been improved and the mathematical model of static stiffness and dynamic stiffness has been developed for the variable stiffness control.The dynamic stiffness is the sum of static stiffness and pressure stiffness.The result based on the experiment and simulation has shown that the air supply pressure is a major factor affecting the static stiffness and dynamic stiffness of elongation type pneumatic compliance actuator.The static stiffness and dynamic stiffness increase with the increasing of supply pressure linearly.

pneumatic compliance actuator；static stiffness；dynamic stiffness；pressure stiffness；air supply pressure

TH138

A

0367-6234（2015）05-0076-05

10.11918/j.issn.0367-6234.2015.05.013

2014-02-14.

国家自然科学基金（51075213）.

滕 燕（1970—），女，博士，副教授.

滕 燕，yanteng@sohu.com.