大型挠性航天器刚柔耦合动特性分析

张巍耀，高晶波，王 聪

（哈尔滨工业大学航天学院，150001哈尔滨）

大型挠性航天器刚柔耦合动特性分析

张巍耀，高晶波，王 聪

（哈尔滨工业大学航天学院，150001哈尔滨）

为研究装载周边桁架式可展开天线的航天器在进行姿态调整时的动态响应特性，建立了航天器动力学模型，并对姿态调整过程的动态响应进行数值求解.首先建立由可展开天线、太阳帆板和中心平台组成的整星有限元模型并求出无约束边界条件下的固有频率和振型.通过有限元模型和Adams联合仿真建立航天器零次刚柔耦合动力学模型并求得姿态调整过程整星的位移和转角以及太阳帆板和可展开天线的动态响应.结果表明:整星的低阶模态特性主要体现在太阳帆板和天线连接杆的变形上，而天线结构无变形；航天器在进行姿态调整时，挠性部件在做大范围整体运动的同时发生显著的结构振动；航天器完成姿态调整后天线几何中心点在平衡位置附近继续振荡.

桁架式可展开天线；模态特性；刚柔耦合；动态响应

周边桁架式天线又称环形可展开天线，主要应用于空间飞行器对地观测任务，是一种极具应用前景的星载天线结构［1］.20世纪90年代美国TRW Astrospace公司研发的空间可展开天线Astromesh是最早应用于工程实际的周边桁架式天线.该天线于2000年12月5日入轨服役［2］.Astromesh由周边桁架、上下柔性索网、调节索和金属反射丝组成，入轨完全展开后口径可达12.25 m，质量仅为55 kg，具有口径可变范围大、收缩率高、变形小、型面精度高等优点.在一定范围内增加天线尺寸不会改变自身结构，单位尺度质量并不成比例增加，反而呈大幅下降趋势［3］.然而反射面预应力求解难度大、型面精度要求过高、结构展开技术过于复杂以及严酷的太空环境等均是周边桁架式天线投入实际应用过程中所面临的难题［4-6］.Mobrem等［7］对 Astromesh空间飞行器的质量特性、固有频率和振型做了详细研究，并讨论了热变形、装配误差和外界扰动对天线膜面精度的影响.Stegman等［8］用口径5 m的Astromesh天线模拟了太空环境的地面热变形试验，得到了膜面温度分布情况以及节点变形位移等实验结果.Chodimella等［9］对满足NASA未来对地观测任务需求的35 m口径Astromesh天线设计方案进行了可行性分析，并研究了天线的结构质量特性以及受到太阳辐射后结构的热变形，提出了一种保持反射面膜面精度的主动控制方案.国内研究人员主要从结构设计与样机试验、反射面预应力计算和天线结构动力学特性等方面展开研究.西北工业大学、浙江大学和哈尔滨工业大学对空间可展开天线的结构设计和展开机理做了相应研究［10-12］.闫军等［13］建立了12.25 m口径天线非线性有限元模型，得到了天线结构的固有频率和振型.西安电子科技大学对天线反射面预应力计算和精度控制做了详尽研究［14］.

航天器在进行姿态调整时会对挠性附件的运动状态产生一定的影响.卫星平台的平移或转动会激发挠性附件的弹性振动.由于结构刚度较低且真空环境下无空气阻尼效应，挠性附件的弹性振动难以抑制.这不仅不利于中心平台的姿态稳定，而且会对挠性附件的正常工作产生有害影响.因此研究航天器调姿过程动态响应特性对挠性附件振动抑制和提高中心平台姿态稳定性具有重要意义.本文首先研究了挠性航天器的结构动力学特性，通过建立有限元模型求解整星的固有频率和振型.利用有限元模型和多体动力学软件Adams建立航天器零次刚柔耦合动力学模型，最后对航天器姿态调整过程动态响应进行了数值仿真求解.

1 动力学模型

挠性航天器的中心平台可视作刚体，挠性附件如可展开天线和太阳帆板等在同中心刚体作整体平移和转动的同时还发生着结构振动，这是典型的刚柔耦合动力学问题［15］.

如图1所示，er为惯性坐标系，eb为浮动坐标系，则航天器任意一点p的位置向量为

式中:r为点p在惯性系下的位置向量；r0为eb原点在惯性系的坐标向量；A为方向余弦矩阵；sp为点p在eb的位置向量；up为相对变形量，采用模态坐标表示为

式中Φp为点p的模态振型矩阵，qf为广义位移.由

式（1）可得柔性体上任意一点p的速度和加速度为

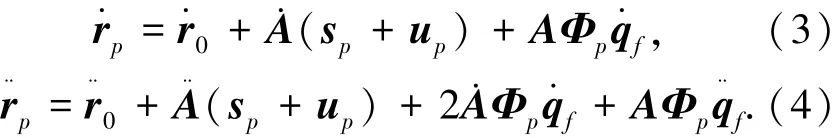
图1 柔性航天器示意

选取浮动坐标系的位置坐标和柔性体的模态坐标作为广义坐标ξ，即

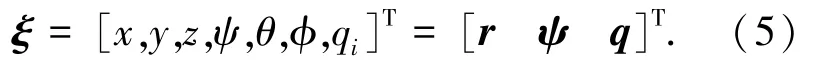
式中i=1，2，…，M.则点p的速度表达式（3）可以表示为

式中B为欧拉角的时间导数与角速度之间的转换矩阵.柔性体的动能和势能为

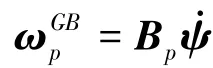
式中M、K和C分别为质量、刚度和阻尼矩阵，Fg为广义重力，λ为拉格朗日乘子，Q为广义外力.

2 有限元模型

［9，16-17］建立口径12.5 m的周边桁架式可展开天线有限元模型.框架采用梁单元等效，前后索网和拉锁使用杆单元等效，预张力通过力密度法求出.反射网采用膜单元等效，其预张力通过降温法获得，即

式中:α为热膨胀系数；T和Tref分别为当前温度和参考温度；ε为预应变.卫星平台有限元模型参照我国东方红3 A建立［18］.当卫星完全展开锁定后，部件之间的连接方式等效为刚性连接.通过采用多点约束将天线和太阳帆板与中心平台连接可以得到整星有限元模型，如图2所示.

自由边界条件下有限元模型一至六阶模态为刚体模态.表1为天线与平台间连杆长度l为7 338 mm时整星七至十二阶固有频率和振型.

图2 整星有限元模型

表1 有限元模型固有频率和振型

在低阶模态中整星振型特性主要体现在太阳帆板和连接杆的变形上，天线无明显的结构变形.事实上从第十八阶模态开始，天线结构才发生明显变形.表2给出了连接杆取不同长度时整星的固有频率.

表2 不同连接杆长度整星固有频率

可以发现，连接杆的增长会使整星的固有频率降低.然而对于第八阶模态而言，连接杆长度增加其固有频率保持不变.这是由于第八阶振型特性主要体现在太阳帆板的变形上，整星和天线保持静止且连接杆和天线无结构变形，因此连接杆长度增加对第八阶固有频率影响较小.

3 刚柔耦合动力学仿真

挠性航天器在轨运行且受到外界激励时的动态响应求解属于刚柔耦合动力学范畴，可以采用有限元+Adams联合求解.即将有限元模型的模态结果导入Adams，建立整星零次刚柔耦合动力学模型.柔性部件上任意一点的运动等效为刚体位移和变形位移的叠加.变形位移采用模态叠加法（式（2））表示.整星在初始时刻为静平衡状态.模型的阻尼为:固有频率在100 Hz以下的模态阻尼率为1%；固有频率在100～1 000 Hz的模态阻尼率为10%；固有频率在1 000 Hz以上的模态阻尼率为100%.

图3为中心平台所受推力，其中F1至F4的推力如图4（a）所示，F5至F8的推力如图4（b）所示.整星在推力的作用下绕质心沿Y轴旋转.图5为整星质心不同方向的位移.图6显示了航天器绕质心沿Y轴旋转的角度.可以发现，在姿态调整过程中，整星质心位置并不改变，仅姿态角发生变化.

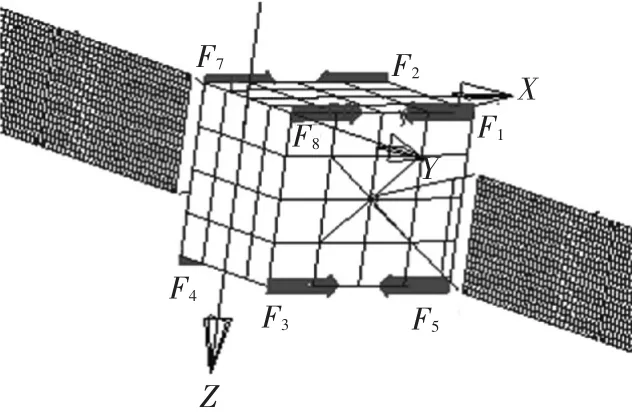
图3 调姿发动机推力布局

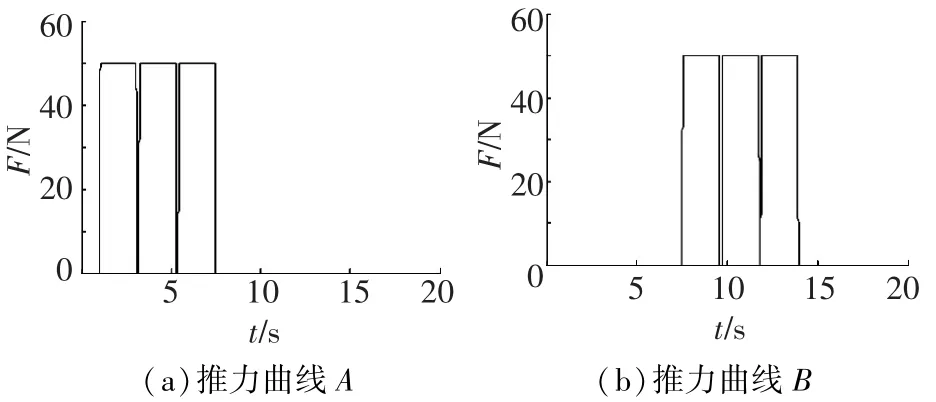
图4 调姿发动机推力曲线

图7、8为连接杆和天线的连接点N1（图2）的位移曲线.当卫星完成调姿后，连接杆继续在平衡位置处振动.图9（a）为整个姿态调整过程天线几何中心的运动轨迹，图9（b）为调姿结束后几何中心的运动轨迹.由于连接杆的弹性振动，在航天器完成调姿后，天线几何中心仍然在一定区域内振荡.

图5 航天器质心位移

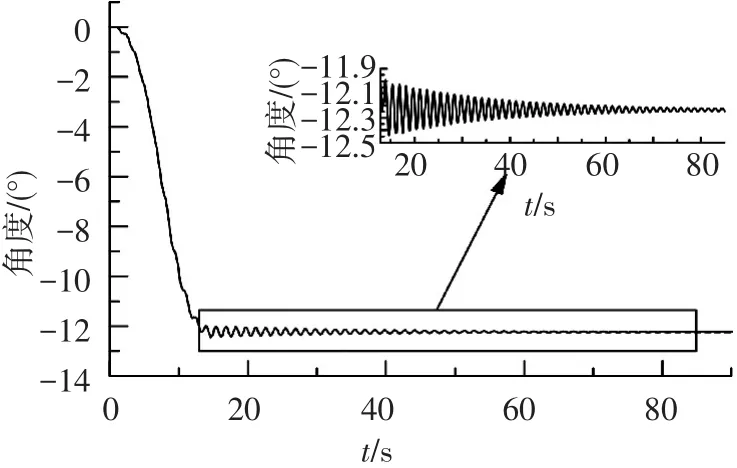
图6 航天器绕质心Y轴方向转角

图8 节点N1在Z方向位移

图9 天线几何中心运动轨迹

图10为姿态调整过程太阳帆板最远自由端的中心处节点N2（图2）X方向振动位移（变形位移）及其傅里叶变换.由节点N2自由振动部分位移曲线的傅里叶变换可以识别整星的第八、九、十阶模态.

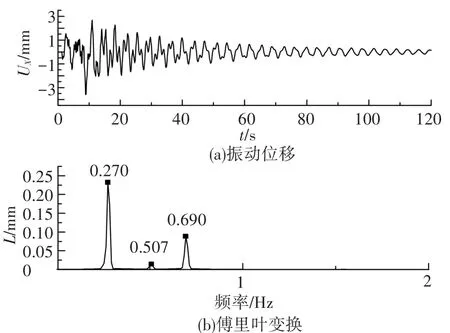
图10 节点N2在X方向振动位移及其傅里叶变换

4 结 论

1）整星的低阶模态特性主要体现在太阳帆板和连接杆的变形上，可展开天线随连接杆作整体刚性运动，无显著结构变形.

2）增加连接杆的长度会使整星固有频率降低.但在第八阶模态中，由于仅太阳帆板发生变形，天线、连接杆与中心平台保持相对静止，其固有频率不随连接杆长度变化而变化.

3）航天器在轨姿态调整会使挠性附件如天线和太阳帆板在做整体运动的同时产生显著的结构变形，且挠性附件的结构振动会在姿态调整过程结束后的一段时间内继续存在.由于连接杆的弹性变形，姿态调整结束后天线几何中心点在平衡位置附近继续保持振荡.

参考文献

［1］SANTIAGO-PROWALD J，BAIER H.Advances in deployable structures and surfaces for large apertures in space［J］.CEAS Space Journal，2013，5:89-115.

［2］THOMSON M W.Astromesh deployable reflectors for Kuand Ka-band commercialsatellites［C］//20th AIAA International Communication Satellite Systems Conference and Exhibit.Reston VA:AIAA，2002:12-15.

［3］THOMSON M W.The Astromesh deployable reflector ［C］//Antennas and Propagation Society International Symposium，1999IEEE.Piscataway:IEEE，1999，3: 1516-1519.

［4］胡海岩，田强，张伟，等.大型网架式可展开空间结构的非线性动力学与控制［J］.力学进展，2013，43（4）: 390-414.

［5］TANAKA H，NATORI M C.Shape control of space antennas consisting ofcable networks［J］.Acta Astronautica，2004，55（3）:519-527.

［6］MEGURO A，SHINTATE K，USUI M，et al.In-orbit deployment characteristics of large deployable antenna reflector onboard engineering trest satellite VIII［J］.Acta Astronautica，2009，65（9）:1306-1316.

［7］MOBREM M，KUEHN S，SPIER C，et al.Design and performance of astromesh reflector onboard soil moisture active passive spacecraft［C］//Aerospace Conference，2012 IEEE.Piscataway:IEEE，2012:1-10.

［8］STEGMAN M D，FEDYK M，KUEHN S.Solar thermal vacuum testing of deployable mesh reflector for model correlation［C］//Aerospace Conference，2010，IEEE.Piscataway:IEEE，2010:1-15.

［9］CHODIMELLA S P，MOORE J D，OTTO J，et al.Design evaluation of a large aperture deployable antenna ［C］//Proceedings of the AIAA/ASME/ASCE/AHS/ ASC Structures，Structural Dynamics，and Materials Conference.Reston VA:AIAA，2006:1-20.

［10］肖勇，王三民.环形可展开大型卫星天线结构设计与研究［D］.西安:西北工业大学，2001.

［11］关富玲，杨玉龙，赵孟良.星载可展开网状天线的网面成形与防缠绕设计［J］.工程设计学报，2006，13 （4）:271-276.

［12］邓宗全，田大可，刘荣强，等.构架式空间可展开天线结构优化参数预测模型［J］.哈尔滨工业大学学报，2011，43（11）:39-43.

［13］闫军，袁俊刚.大型空间抛物面天线非线性有限元建模分析［C］//全国结构动力学学术研讨会论文集.杭州:中国振动工程学会，2007:262-267.

［14］杨东武.星载大型可展开索网天线结构设计与型面调整［D］.西安:西安电子科技大学，2010.

［15］SHABANA A A.Flexible multibody dynamics:review of past and recent developments［J］.Multibody System Dynamics，1997，1（2）:189-222.

［16］DATASHVILI L，ENDLER S，WEI B，et al.Study of mechanical architecturesoflargedeployable space antenna apertures:from design to tests［J］.CEAS Space Journal，2013，5:169-184.

［17］肖勇，王三民，陈国定.大型卫星天线系统固有模态的有限元分析［J］.机械设计与制造，2006（7）: 1-2.

［18］朱毅麟.中国空间技术研究院的标准化卫星平台［J］.航天器工程，2007，16（1）:10-17.

（编辑 张 宏）

Rigid-flexiblecoupling dynamic analysis of the spacecraft installing large flexible attachments

ZHANG Weiyao，GAO Jingbo，WANG Cong
（School of Astronautics，Harbin Institute of Technology，150001 Harbin，China）

The mechanical model of the spacecraft equipped with the hoop truss deployable antenna was developed and its characteristic of dynamic responses in the stage of attitude adjustments are solved numerically.Firstly the FE model composed of the central platform，solar panels and deployable antenna was established and its natural frequencies and mode shapes in the unconstrained condition were calculated.By the union simulation of FEM and Adams the zero-order rigid-flexible coupling dynamic model of the spacecraft was set up，and then the model＇s translation and rotation angle as well as dynamic responses of solar panels and the deployable antenna in the process of attitude adjustments were given.Results show that the lower order mode shapes of the model are mainly from the antenna′s connecting link and solar panels′deformation while the antenna′s shape is fixed.In the procedure of attitude adjustments，the spacecraft′s flexible attachments can deform elastically along with rigid motions and the vibration is rather serious.The antenna′s geometry central point keeps vibrating around the equilibrium position even though attitude adjustments are finished.

hoop truss deployable antenna，modal characteristic，rigid-flexible coupling，dynamic responses

V414.5

A

0367-6234（2015）05-0046-04

10.11918/j.issn.0367-6234.2015.05.008

2014-07-01.

张巍耀（1990—）男，硕士研究生；

王 聪（1966—）男，教授，博士生导师.

高晶波，gaojb@hit.edu.cn.