SRGM中TE建模机制与模型比较分析
张 策,孟凡超2,崔 刚,刘宏伟,官红玉2
(1.哈尔滨工业大学计算机科学与技术学院,150001哈尔滨;2.哈尔滨工业大学(威海)计算机科学与技术学院,264209山东威海)
SRGM中TE建模机制与模型比较分析
张 策1,2,孟凡超2,崔 刚1,刘宏伟1,官红玉2
(1.哈尔滨工业大学计算机科学与技术学院,150001哈尔滨;2.哈尔滨工业大学(威海)计算机科学与技术学院,264209山东威海)
针对当前与软件可靠性增长模型SRGM(software reliability growth model)紧密相关的测试工作量TE(testing effort)的研究现状,以及全面评价测试工作量函数TEFs(testing effort function)性能的需要,对SRGM下TE相关的建模与模型比较问题进行深入研究.分析了近40年的TE发展历程与内容演变,对其与测试成本间关联进行剖析;对典型的TEFs进行了全面梳理与述评;研究了考虑TE的SRGM建模过程;针对8个典型的TEFs,在已发表的4组数据集上进行了深入的性能比较与评述.研究结果表明,有效的TEF可为基于SRGM的可靠性相关研究提供重要决策支持,对考虑TE 的SRGM进行综合评价是后续研究的关键.
软件可靠性;测试工作量;测试工作量函数;软件可靠性增长模型;成本
软件测试中,在测试工作量 TE(testing effort)的不断消耗下,故障不断被检测和排除掉,总故障数量a(t)保持下降趋势,使得软件可靠性R(t)获得增长.TE的消耗代表着测试成本的支出,而软件测试通常受制于有限的预算限制;同时,TE的消耗进度也应该受到有效的控制.以可靠性为目标之一的测试过程应被合理的管控,低效与冗余的测试可能导致额外的成本开销[1],对成本管控和最优发布时间决策带来隐患.TE对以软件可靠性增长模型 SRGM(software reliability growth model)为基础的可靠性工程相关研究形成了重要支撑.
本文对TE的建模过程,考虑TE的SRGM建模,以及现有的测试工作量函数TEF(testing effortfunction)评价进行了综合研究与评述.首先给出了有关概念,对TE的发展历程与研究内涵进行分析,并对当前TEFs进行了全面梳理;然后对考虑TE的SRGM建模机制进行剖析;最后在4个已发表的数据集上对8个典型的TEFs进行了全面比较.
1 定义与相关背景
1.1 相关定义
定义1 测试工作量TE[2-4]用以描述软件测试过程中所消耗的资源,可表示为测试中所花费的测试案例与分析数据的数量、CPU时间、时钟时间、日历时间数或者人力费等.
定义2 测试工作量函数TEF是采用数学表达式的形式对测试过程中TE的消耗进行描述的数学工具.
定义3 软件可靠性增长模型SRGM[5-6]是在软件开发的测试阶段与操作运行阶段,基于失效数据,描述软件测试过程中累积检测或修复的故障数量,TE与测试时间等的数学关系,是实现建模软件可靠性提高过程的数学工具.
1.2 TE发展历程变迁
与TE紧密相关的研究最早可追溯到文献[7],近40年来科研人员对TE的研究伴随着SRGM的广泛应用得到了足够重视,图1给出了TE的发展历程及研究内容的演变.可以看出,自20世纪90年代后期始,TE与SRGM开始融合,并在以可靠性为核心的研究中占有重要地位.

图1 TE发展历程与研究内容演变
与SRGM相关的基于TE的研究主要包括: 1)考虑TE进行SRGM的建模,提高模型的有效性;2)进行TE的分配与管控,实现测试过程中对以可靠性为核心的指标调整;3)建立成本模型,在“成本+可靠性”的综合统筹下,实现软件的预期发布.
1.3 讨论:TE与测试成本的区别与关系
在TE与测试成本的关系上,二者紧密相关但存有明显区别:TE的本质是如其定义中所述的测试资源;测试成本指测试过程中所花费的总成本C(T).虽有文献[8-9]认为TE就是测试成本,但显然是片面的,因为只是全部软件测试成本中包含了TE花销的成本而已[10].例如,测试成本在文献[1,5]中被采用


2 TEFs类别与讨论
软件测试中,TE被不断消耗的过程表示了失效被如何有效地检测到[11].TEF能被用来描述测试过程中的工作剖面,是对(测试)资源消耗的一种定量描述,存在多种形式.
2.1 Yamada Exponential、Yamada Rayleigh与Yamada Weibull型TEF:基于微分方程法



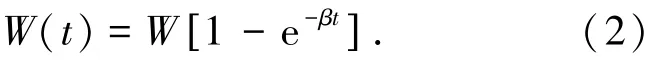

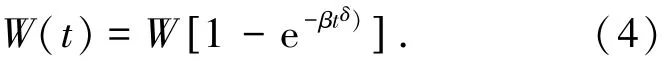
显然,式(2)与式(3)是式(4)的一种特殊情况.
2.2 Exponential Weibull型TEF
在文献[13]的基础上,文献[14-15]提出了一般化的EW TE(Exponentiated Weibull:指数威布尔型)对软件失效行为进行预测,并认为EW TEF在评估可靠性过程中表现优异,有较强的适应性与柔韧性.
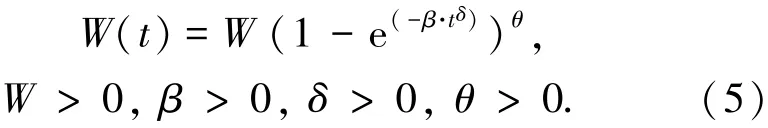
式中:β为比例调节参数,δ、θ分别为形状参数.对此3个参数进行讨论,得到表1中结果.
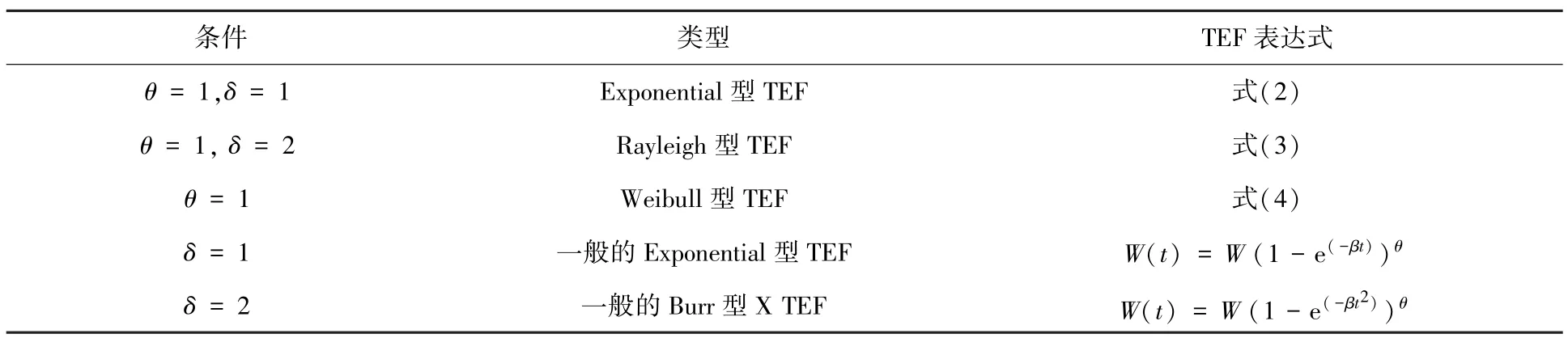
表1 EW TEF特定条件下演化结果
2.3 泛Logistic型TEF
作为Rayleigh TEF的替代,Logistic TEF最早由Parr[16]于 1980年提出,后被广泛研究.文献[17]认为Weibull类型的TEF当δ>3时会出现所谓的“峰现象”,并不符合实际软件测试,据此文献[1,3,5,10,17-18]提出了Logistic TEF、一般化的Logistic TEF和更一般化的Logistic TEF,分别为
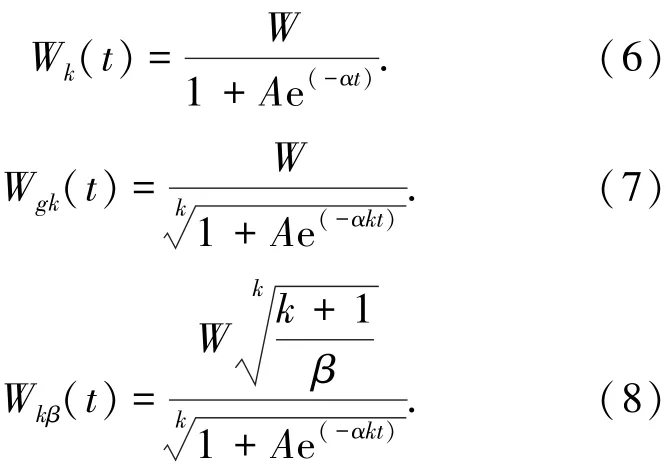
此外,在文献[19]中提出Log-Logistic TEF为
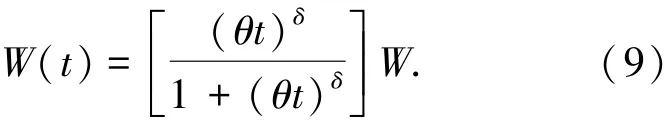
整体而言,由于Logistic TEF具有S型的变化趋势,可描述多种TE消耗情形,得到了广泛应用.
2.4 讨论:TEFs必要说明
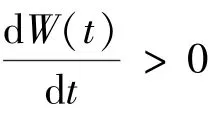
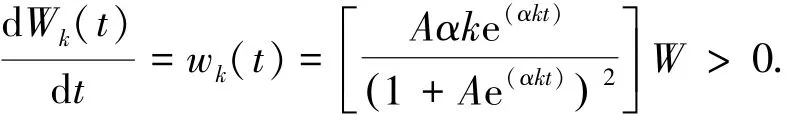

现有TEF模型在数学表达式上存在很大差异,因而其在不同的数据集的表现上一定会存在较大不同.
3 考虑TEF的SRGM建模研究
在SRGM的相关研究中,对TE的研究均是借助TEF来进行的,主要涵盖SRGM建模、TE管控和最优发布3个方面上,且前者是后两者研究的基础.TE为3个问题的研究提供了必要的支撑,使得所建立的SRGM更加考虑到实际测试因素,对TE的管控更为高效,最优发布具备决策参考支持,并最终为获得预期的可靠性目标提供重要保障.在文献[6]中,已对TE分配与调控和最优发布策略进行分析,这里从略.
3.1 考虑TEF的SRGM基本建模方法
测试阶段软件可靠性与故障检测与修复所花费的TE紧密相关[11],通常所建立的SRGM中直接包含有TEF.例如,典型的考虑TE到SRGM中的建模方法如下[1-3,5,10-11,15,17-18,21-25]:式中:m(t)为[0,t]内累计检测到的故障数量,a为软件中的总故障个数.该微分方程建立的假设基础为:[0,t]内累计检测到的故障数量与当前剩余的故障数量下所花费的TE时的故障检测率r(t)成比例.
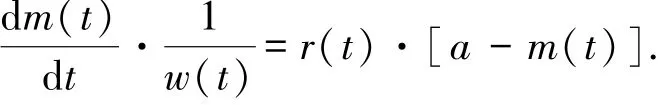
3.2 讨论:不完美排错下的建模
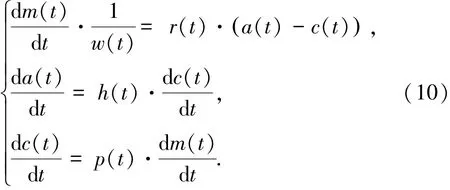
由于测试环境中随机因素的影响,考虑TEF 的SRGM应向不完美排错研究[12,25]的趋势转变,将更多的实际因素融入进来.为此,文献[20,26]给出了更加一般化且具有较强柔韧性的框架模型,支持不完美排错与TE的综合考量为式中:a(t)、c(t)分别为[0,t]内软件中总的故障数量和累计修复的故障数量;h(t)、p(t)分别为故障引入比例函数和故障改正比例函数.式(10)描述了更多的测试细节,可以演变为多个现有的模型;同时,在现有研究的基础上给出了改进的初值不为零的Logistic TEF为

基于此所获得的SRGM在性能上优于其他模型[20].
由于TEF的引入,测试过程中可以借助调整TE的方式来影响m(t),使得测试中的可靠性能向预期增长(测试阶段的可靠性)为

相比于传统SRGM,考虑TEF的SRGM表现得更为优秀,这可以被解释为TEF的偏差在它的基本概念中已经考虑到了人力因素和不确定性.
软件发布不仅要考虑到可靠性要求,成本因素也至关重要[18],“成本+可靠性”综合标准[15]已成为最优发布的统筹考虑.
4 TEF性能验证与分析
4.1 性能评价标准与数据集选择
在对模型与真实数据的拟合评价上,MSE,MEOP,Variation,RMS-PE,TS和BMMRE常被用来作为度量的选择,这些数值越小表明拟合效果越好,R-square越接近于1越好;RE被作为模型对未来数据预测的评价标准,RE越趋近于0表明预测效果越好.式中:K为数据样本数量大小;p为参数个数;Wi为到ti时实际观测到的数据;W(ti)为到ti时利用模型得到的估算值.

4.2 参与比较的TEFs
这里,本文选取典型的8个TEFs模型用于比较,如表3所示,并依次编号为①~⑧.其中③~⑤为由⑥中的模型演化而来.
4.3 TEF性能差异化比较
首先,对表3中的TEFs在DS1~DS4上进行参数拟合,并画出了TEFs在4组数据集上的实际TE消耗曲线与W(t)之间的拟合情况,如图2所示.
1)在DS1、DS2和DS4上8个TEFs与实际的TE消耗情况拟合的较好,而且W(t)曲线基本呈现出通过原点的斜率为k的直线态势.例如,从图2的4幅图中均可以看出,W(t)= W 1-e-φt()的曲线接近于通过原点的线性形状.造成这种现象的原因以及斜率k的近似计算可解释为:对于这些数据集其估计得到的参数值非常的小(例如,DS1中,=0.000 590 895 2).此时,可以得到,因而呈现线性关系,其斜率为k=Wφ.

表2 TE数据集遴选—真正的实际应用案例

表3 参与比较的TEFs
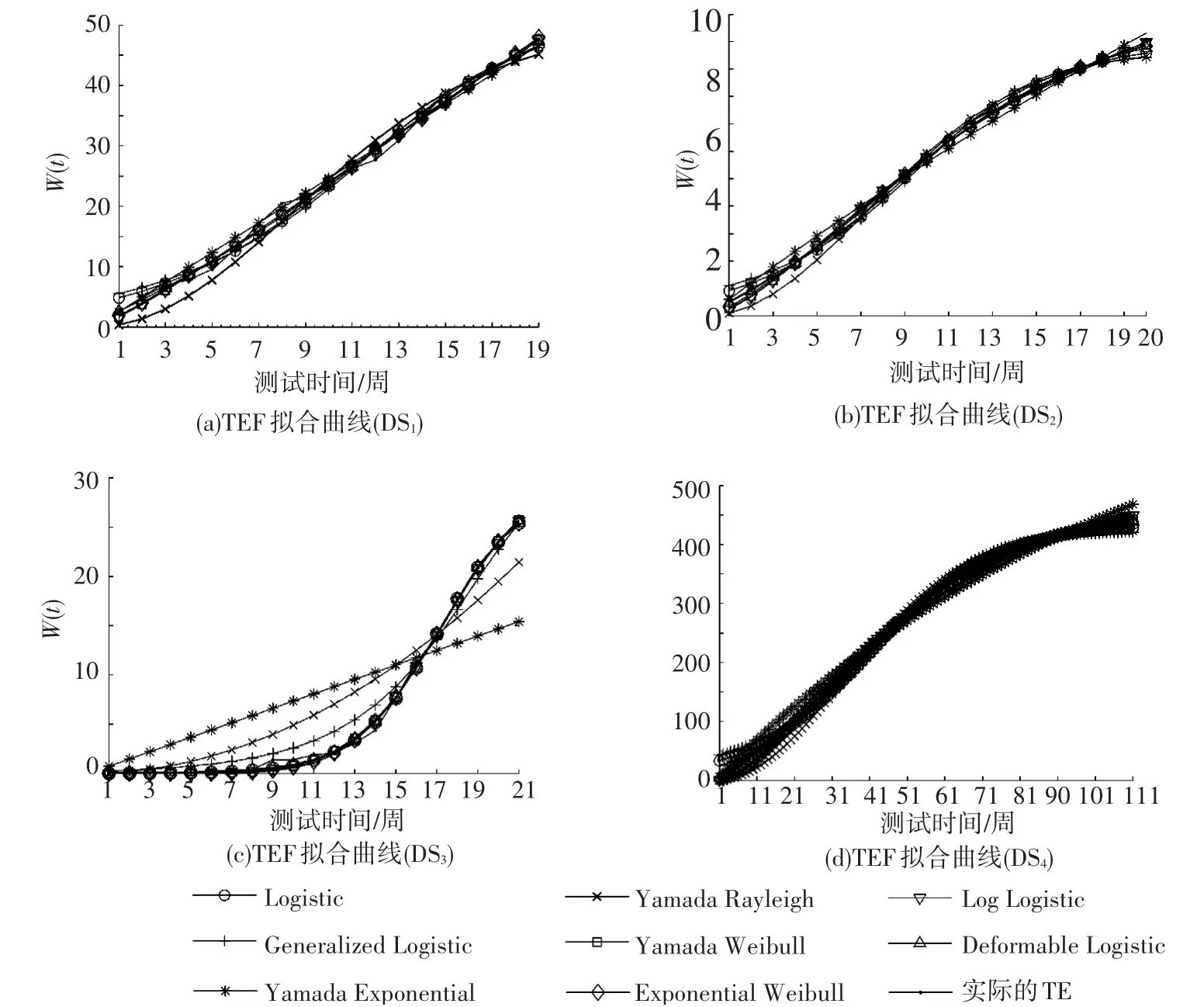
图2 TEF在4组数据集上的拟合曲线
2)在DS3上,TEFs的拟合差别比较明显,其中②、③和④出现了较大的偏差,其余模型拟合效果较好.这主要是由于DS3中实际的TE数据与②、③和④模型函数的本质差距较大造成的.
为了进一步区分TEFs在数据集上的拟合差异,本文计算了具体的比较标准值,结果如表4所示.
为了清晰地显示出TEFs在4组数据集上不同标准上的差异,表4中每个数据集上,性能值最优的采用*的形式标出,其次采用双下划线的形式标出,再次采用单下划线的形式标出.由表4可以明显看出:
1)8个TEFs在4组数据集上的比较结果中,第⑧个TEF模型(变形Logistic型)的结果值是最优的:其在28(4*7)个性能值中有26个数值是最优的,且另外2个是次优的.
2)其次是第⑥个TEF模型(一般指数型),其有17个在剩余7个TEF模型的比较标准中最优,另有7个标准是次优的.
3)再次是第⑤个TEF模型(Yamada Weibull型),在除了第⑧个模型外剩余的6个模型的比较标准中,有19个是最优的.
因而,本文可以充分地认为,第⑧个TEF个可以最好的描述多种情况的TE消耗,这可以解释为变形Logistic型具有先增后降的S型变化趋势,符合多数测试工作量的实际消耗情况.
接下来,本文画出了TEFs在4个数据集上的预测曲线RE,结果如图3所示.从图3中可看出: 在DS1上,各个模型的预测差异较大,其中{④、②、①}预测性能不理想,逐渐下降,其余模型效果较好;在DS3上,8个模型的预测差异最大,其中偏离中心值最大的依次是{③、④、⑦、①、②},其余的相对较好,但⑧表现得并不优秀,⑥最优秀;在DS2上,各个模型的预测差异整体较小,除较差的{③、①、②、④}性能依次降低外,其余4个模型预测效果较好;在DS4上,从表现上,可以分为4组,其性能依次降低为{⑥、⑧}、{①、②、④}、{⑦、⑤}及{③}.
此外,在图3中还需指出:1)有些模型的RE曲线会出现很高的“突起”,例如,图3(a)(DS1)与图3(c)(DS3)中.这主要是由于实际的TE数据集中有变动点CP(change-point)而造成的,例如测试环境的改变就会引发CP的出现,使得CP前后数据值差距较大,从而引起“突起”现象;2)绝大部分模型在前2/3左右的时间内其预测性能一般,之后逐渐趋向良好.这主要是由于模型中参数较多,只有当数据集增长到一定规模时,才能使模型中的参数逐渐获得接近于最终拟合值的良好效果.
4.4 TEF性能差异化分析
综合上述实验与分析,从8个TEFs在4组数据集上的度量与预测效果比较的结果可得到如下结论:
1)TEF对测试数据集的依赖非常强.由于不同数据集在数据收集方式等上的差异,使得8个TEFs在有些数据集上表现较好,相反在另外一些数据集上表现一般,差异较大.例如,在DS3上8 个TEFs的拟合偏差较大;在DS1,DS2和DS4上各个模型的拟合差异比较小.

图3 TEFs在4组数据集上的RE曲线比较
2)从拟合与预测的整体效果来看,⑧、⑥、⑤模型的综合性能表现得最优.其余模型中有的拟合效果较好,但其 RE预测曲线并不理想;或反之.
3)基于上述分析,从现有可得的包含TE的失效数据集DS1~DS4可以看出,除⑧、⑥、⑤模型外(仅限在此4组数据集上,还需更多数据集实例去验证),并不存在一个最优的TEF能够对测试资源的消耗进行精准的管控(度量与预测).因此,在实际应用中,要应该依据数据集上的差异,合理选择TEF进行应用.
4)实际应用中,可以采用“测试数据转换”的方法,这能够从现有数据集上获得较多的测试数据.例如,一个较为简单的做法是,将现有的以周为单位的测试数据转换为以若干小时为单位,这样数据集的规模会增大,能够缓解“小数据集”带来的不便.
5 结 论
1)TE表征了测试过程中消耗的资源,与SRGM的建模结合促进了TE在成本与可靠性工程研究中的重要地位.
2)选择与提出合理的TEF可对测试资源进行有效管控,可改善基于SRGM所获取的可靠性相关指标特征,从而为建立准确的成本模型与进行最优发布提供决策支持.
3)从对测试资源的描述能力来评价TEF过于单一,现有测试的目的已经从传统的排除故障转化到不断提高可靠性为目标,因为软件发布的主要标准之一是其可靠性达到预期.为此,后续研究中,应对涵盖TEF的SRGM整体性能进行更为综合的验证与评价.
[1]HUANG C Y,LYU M R.Optimal release time for software systems considering cost,testing-effort,and test efficiency[J].IEEE Transactions on Reliability,2005,54(4):583-591.
[2]JHA P C,GUPTA D,YANG B,et al.Optimal testing resource allocation during module testing considering cost,testing effort and reliability[J].Computers& Industrial Engineering,2009,57(3):1122-1130.
[3]HUANG C Y,LYU M R.Optimal testing resource allocation, and sensitivity analysis in software development[J].IEEE Transactions on Reliability,2005,54(4):592-603.
[4]OHTERA H,YAMADA S.Optimal allocation and control problems for software-testing resources[J].IEEE Transactions on Reliability,1990,39(2):171-176.
[5]HUANG C Y.Cost-reliability-optimal release policy for software reliability models incorporating improvements in testing efficiency[J].Journal of Systems and Software,2005,77(2):139-155.
[6]张策,崔刚,刘宏伟,等.软件测试资源与成本管控和最优发布策略[J].哈尔滨工业大学学报,2014,46(5):51-58.
[7]BOEHM B W.Software Engineering Economics[M].New Jersey:Prentice Hall PTR,Upper Saddle River,1981.
[8]GOKHALE S S,LYU M R,Trivedi K S.Incorporating faultdebugging activities into software reliability models:a simulation approach[J].IEEE Transactions on Reliability,2006,55(2):281-292.
[9]BEMAN O,CUTLER M.Resource allocation during tests for optimally reliable software[J].Computers& Operations Research,2004,31(11):1847-1865.
[10]HUANG C Y,LO J H.Optimal resource allocation for cost and reliability of modular software systems in the testing phase[J].Journal of Systems and Software,2006,79(5):653-664.
[11]AHMAD N,KHAN M G M,RAFI L S.A study of testing-effort dependent inflection S-shaped software reliability growth models with imperfect debugging[J].International Journal of Quality & Reliability Management,2010,27(1):89-110.
[12]KAPUR P K,GOSWAMI D N,BARDHAN A,et al.Flexible software reliability growth model with testing effortdependent learning process[J].Applied Mathematical Modelling,2008,32(7):1298-1307.
[13]YAMADA S,OHTERA H,NARIHISA H.Software reliability growth models with testing-effort[J].IEEE Transactions on Reliability,1986,35(1):19-23.
[14]BOKHARI M U,AHMAD N.Software reliability growth modeling forexponentiated Weibullfunctionswith actual software failures data[J].Advances in computer science and engineering: reports and monographs,2007,2:390-396.
[15]AHMAD N,BOKHARI M U,QUADRI S M K,et al.The exponentiated Weibull software reliability growth model with various testing-efforts and optimal release policy[J].International Journal of Quality&Reliability Management,2008,25(2):211-235.
[16]PARR F N.An alternative to the Rayleigh curve model for software development effort[J].IEEE Transactions on Software Engineering,1980(3):291-296.
[17]KUO S Y,HUANG C Y,LYU M R.Framework for modeling software reliability,using various testingefforts and fault-detection rates[J].IEEE Trans on Reliability,2001,50(3):310-320.
[18]HUANG C Y,KUO S Y.Analysis of incorporating logistic testing-effort function into software reliability modeling[J].IEEE Transactions on Reliability,2002,51(3):261-270.
[19]GOKHALE S S,TRIVEDI K S.Log-logistic software reliability growth model[C]//Proceedings of 3rdIEEE International Symposium on High-Assurance Systems Engineering.Washington,DC:IEEE,1998:34-41.
[20]ZHANG C,CUI G,MENG F C,et al.A study of optimalrelease policy for SRGM with imperfect debugging[J].Journal of Engineering Science and Technology Review,2013,6(3):111-118.
[21]LIN C T,HUANG C Y.Enhancing and measuring the predictive capabilities of testing-effort dependent software reliability models[J].Journal of Systems and Software,2008,81(6):1025-1038.
[22]HUANG C Y.Performanceanalysisofsoftware reliability growth models with testing-effort and changepoint[J].Journal of Systems and Software,2005,76(2):181-194.
[23]HUANG C Y,KUO S Y,LYU M R.An assessment of testing-effort dependent software reliability growth models[J].IEEE Transactions on Reliability,2007,56(2):198-211.
[24]AHMAD N,KHAN M G M,QUADRI S M K,et al.Modelling and analysis of software reliability with Burr type X testing-effort and release-time determination[J].Journal of Modelling in Management,2009,4(1): 28-54.
[25]AHMADA N,KHANB M G M,RAFIB L S.Analysis of an inflection S-shaped software reliability model considering log-logistic testing-effortand imperfect debugging[J].Int.J.Comp.Net.Sec,2011,11(1): 161-170.
[26]ZHANG C,CUI G,LIU H W,et al.A unified and flexible framework of imperfect debugging dependent SRGMs with testing-effort[J].Journal of Multimedia,2014,9(2):310-317.
[27]OHBA M.Software reliability analysis models[J].IBM Journal of research and Development,1984,28(4): 428-443.
[28]WOOD A.Predicting software reliability[J].IEEE Computer,1996,29(11):69-77.
[29]MUSA J D,IANNINO A,OKUMOTO K.Software reliability:measurement,prediction,application[M].New York:McGraw Hill,1987.
[30]PHAM H.SoftwareReliability[M].Singapore: Springer,2000.
(编辑 张 红)
Overview of modeling of TE in SRGM and comparisons for models
ZHANG Ce1,2,MENG Fanchao2,CUI Gang1,LIU Hongwei1,GUAN Hongyu2
(1.School of Computer Science and Technology,Harbin Institute of Technology,150001 Harbin,China;2.School of Computer Science and Technology,Harbin Institute of Technology at Weihai,264209 Weihai,China)
To systematically reveal the state of art of testing effort(TE)related to software reliability growth model(SRGM)and to evaluate performances of testing effort function(TEFs),modelling of TE dependent SRGM and comparisons for models are studied in this paper.More specifically,firstly,research evolution of TE is summarized since the early 1978 s,and the relation between TE and test cost is analyzed.Then,current TEFs are reviewed and discussed,and modeling process of SRGM incorporating TE is illustrated.Performances of 8 TEFs are evaluated and compared by 4 failure data sets published.Finally,conclusions indicate that appropriate TEF can support decision for research of reliability based on SRGM and evaluating SRGM incorporating TE would be worthwhile in future.
software reliability;testing effort(TE);testing effort function(TEF);software reliability growth model(SRGM);cost
TP311
A
0367-6234(2015)05-0032-08
10.11918/j.issn.0367-6234.2015.05.006
2014-06-03.
国家科技支撑计划资助(2013BA17F02);山东省科技攻关项目(2011GGX10108,2010GGX10104).
张 策(1978—),男,讲师;博士研究生;
崔 刚(1949—),男,教授,博士生导师;
刘宏伟(1971—),男,教授,博士生导师.
张 策,zhangce@hitwh.edu.cn.

