高斯粒子滤波的惯性/GPS紧组合算法
于永军,徐锦法,熊 智,张 梁
(1.直升机旋翼动力国家级重点实验室(南京航空航天大学),210016南京;2.南京航空航天大学导航研究中心,210016南京)
高斯粒子滤波的惯性/GPS紧组合算法
于永军1,徐锦法1,熊 智2,张 梁1
(1.直升机旋翼动力国家级重点实验室(南京航空航天大学),210016南京;2.南京航空航天大学导航研究中心,210016南京)
为提高组合导航系统的可靠性,针对以伪距、伪距率残差为量测信息的紧组合算法会带来线性化误差的缺点,推导了基于伪距、伪距率的非线性紧组合模型.针对紧组合系统状态维数高导致粒子滤波实时性差的问题,提出基于线性非线性结构分解的高斯粒子滤波算法,对状态方程中的非线性和线性部分利用高斯粒子滤波和经典卡尔曼滤波分别进行递推,有效降低了系统的运算量.仿真结果表明,使用改进的紧组合滤波算法系统定位精度相比线性化紧组合算法提高一倍.
惯性导航;组合导航;紧组合;非线性滤波;高斯粒子滤波
涵道式垂直起降无人飞行器以其体积小、重量轻、噪声低、安全性高、适应飞行器高速和小型化的发展需求等特性,目前已经成为垂直起降无人机领域研究的重点和热点[1-3].当前以惯性导航系统为基础的基于卡尔曼滤波理论的惯性/GPS组合导航技术在无人飞行器自主导航领域得到了广泛应用[4-5].以速度、位置组合为特征的捷联惯导/GPS松组合方式虽然组合方案简单、实现较为容易,但当载体进行高动态机动或GPS接收机受到环境干扰时,系统精度将急剧下降,可靠性和抗干扰能力较差[6-7].相对于松组合方式,紧组合中GPS接收机只需提供更为原始、直接的星历和伪距、伪距率数据,无需直接提供载体的速度、位置信息.紧组合方式中GPS接收机和惯性导航系统相互辅助,从而使系统获得更好的导航性能[8-9].
随着捷联惯导/GPS组合导航系统应用条件的日益苛刻,非线性估计理论应用于SINS/GPS组合导航系统逐渐成为研究的热点[10-11].粒子滤波技术由于理论上适用于任意非线性系统的状态估计,因此在非线性组合领域日益受到关注[12-13].目前粒子滤波已在SINS/GPS组合导航系统的位置及姿态估计、SINS/GPS初始对准等方面得到了成功应用[14-15].
粒子滤波虽然能够有效解决SINS/GPS组合导航系统中的非线性滤波问题,但实际应用中随着系统维数增加,为保证粒子滤波的收敛,对高维系统必须采用更多数量的粒子,粒子数量随系统维数增加急剧增加[16].因此,粒子滤波的实时性严重制约了其在SINS/GPS组合导航系统中的应用[17-18].
针对紧组合导航系统特点,本文推导了基于伪距、伪距率的紧组合非线性滤波模型,去除了伪距、伪距率残差线性化过程的线性化误差.针对紧组合系统状态量多导致粒子滤波实时性差的问题,提出了基于线性非线性结构分解的粒子滤波算法,在保证组合滤波实时性的同时,有效提高滤波精度.
1 SINS/GPS紧组合非线性模型
1.1 系统状态方程
导航系选为“东北天”坐标系,捷联惯性导航系统机体系(b)到导航系(n)转动四元数Q的微分方程可以写成[19]


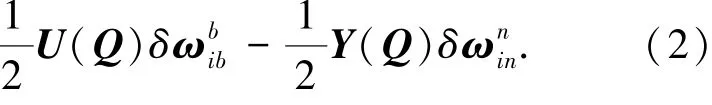
其中δQ=[δq0,δq1,δq2,δq3],U(Q)、Y(Q)详细表述参见文献[19].
不考虑重力加速度误差项,速度误差模型可表示为
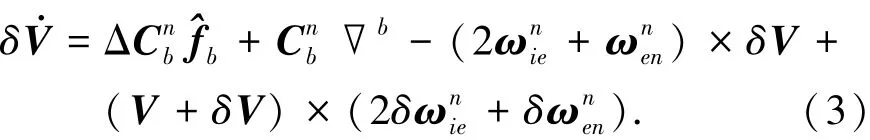
其中δV=[δVE,δVN,δVU]
位置误差模型可表示为
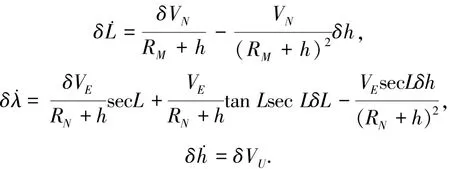
其中RM,RN为地球曲率半径.
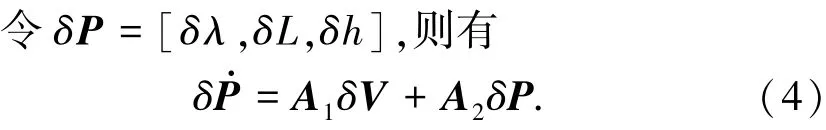
与松组合相比,紧组合的状态方程在松组合的基础上,增加了GPS的误差状态,即:等效时钟误差相应的距离率δtu以及等效时钟频率误差相应的距离率δtr u.δtu与δtr u的微分方程如下:

由此,系统状态量如下:
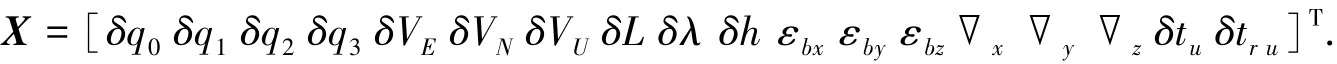
其中,εbx、εby、εbz为陀螺零偏,∇x、∇y、∇z为加速度计零偏.
分析式(2)~(4)可以看出,系统状态方程非线性模型中,仅有速度误差模型是非线性的,而姿态、位置和GPS钟差等模型依然是线性的,因此,系统状态量可以表示成如下形式:

其中:
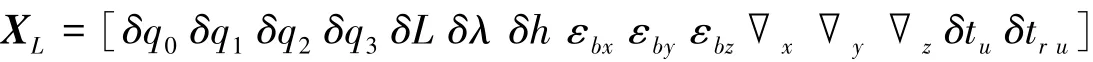
表示系统的线性部分,而XNL=[δVE,δVN,δVU]表示系统的非线性部分.
由此,系统状态方程可以表述成如下形式:
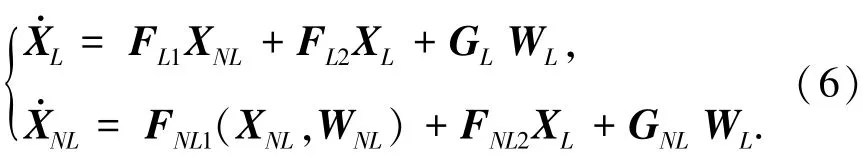
其中:FNL1,FNL2为系统非线性部分的转移矩阵;FL1,FL2为系统线性化部分的转移矩阵;GL,GNL为噪声系数矩阵.
1.2 伪距量测方程
GPS接收机输出的对应某颗卫星i的伪距值为
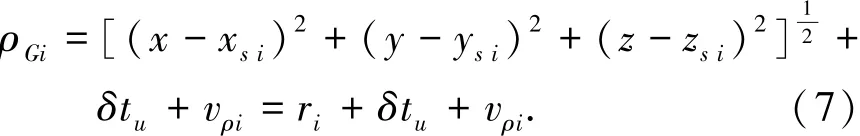
其中:(x,y,z)为载体在ECEF坐标系上的位置真值;(xs i,ys i,zs i)为GPS第i颗卫星在ECEF坐标系上的位置;vρi为伪距测量误差.
载体真实位置(λ,L,h)与惯性导航系统输出位置(λI,LI,hI)有如下关系:
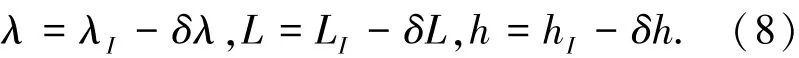
根据下式:
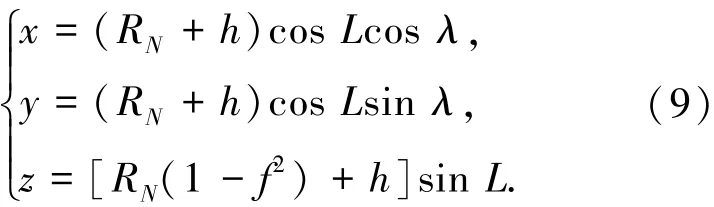
将载体真实位置(λ,L,h)转换到ECEF坐标系并代入式(7),可得到如式(10)的伪距量测方程.


1.3 伪距率量测方程
与伪距量测方程类似,GPS接收机输出的对应某颗卫星i的测量伪距率为

载体真实速度(ve,vn,vu)与惯性导航系统输出速度(veI,vnI,vuI)有如下关系:
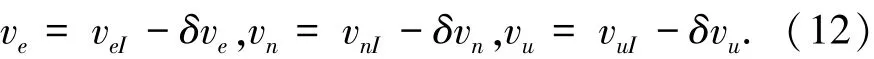
根据坐标系的转换关系,地理系速度与ECEF坐标系的速度转换关系为
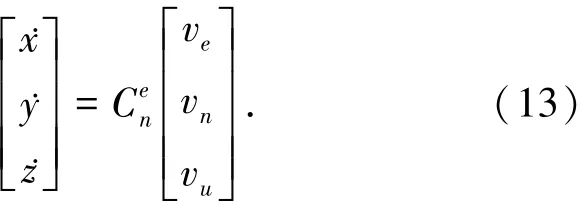

根据式(13)将载体速度(vE,vN,vU)转换到ECEF坐标系,并代入式(11),可得到伪距率量测方程:
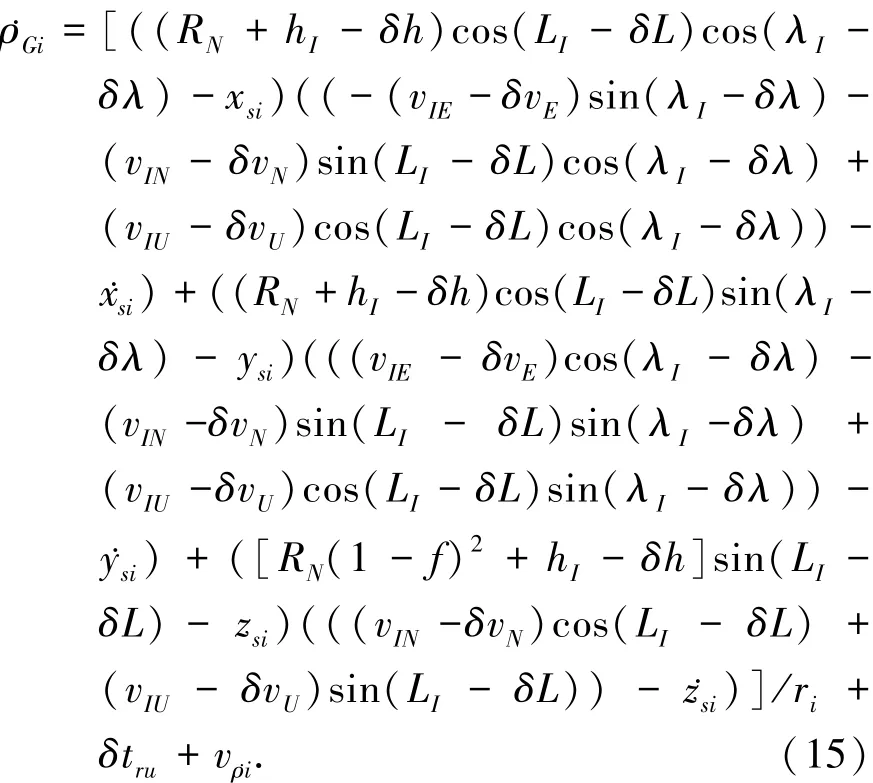
根据式(10)和式(15),可以得到第i颗卫星的量测方程为
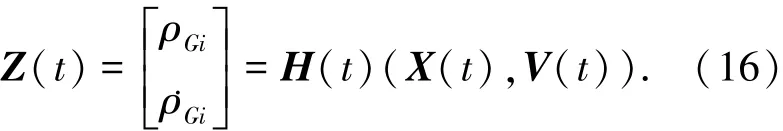
2 基于结构分解的高斯粒子滤波算法
针对形如
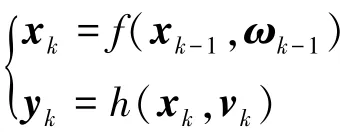
的非线性系统,高斯粒子滤波分为抽取采样点、时间更新和量测更新3个步骤.假设k-1时刻的后验概率密度已知:
第一步,根据k-1时刻滤波结果抽取采样点:

第二步,利用状态方程进行时间更新:
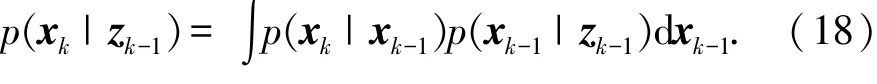
并确定粒子权值
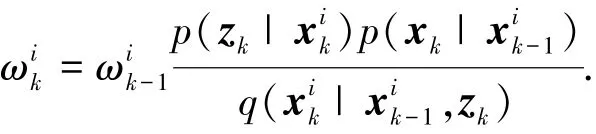
其中p(·)表示概率密度,q(·)表示重要性密度函数.
第三步,根据量测方程进行量测更新:

其中Ck为归一化因子,并利用式(20)构造新的粒子

针对由式(6)和式(16)构成的GPS/INS紧组合导航系统,由于系统方程中仅有速度误差为非线性,因此将非线性系统的更新过程按照如下步骤分解为非线性方程和线性方程分别进行:
第一步,根据式(17)抽取采样点xk,并根据式(6)将 xk分解为线性部分 xkL和非线性部分xkNL;
第二步,根据式(6)和式(18),对xkNL进行高斯粒子滤波时间更新得到x(k+1)NL,根据式(6),利用经典卡尔曼滤波对xkL进行时间更新x(k+1)L;
第三步,将x(k+1)NL和x(k+1)L合并构成非线性系统的状态一步预测x(k+1),并利用UT变换求解一步预测均方误差;
第四步,利用式(19)和式(21)进行量测更新,并对x(k+1)进行修正.
3 仿真验证
根据上述组合方案,对SINS/GPS紧组合算法进行仿真.设惯性导航系统的陀螺常值漂移为0.1°/h,加速度计零偏为3×10-4G.GPS接收机伪距白噪声5 m,伪距率白噪声0.2 m/s.捷联惯导周期为5 ms,GPS输出周期为1 s,滤波周期为1 s.仿真时间为3 600 s.粒子滤波粒子数取为1 000个.
载体的典型机动动作设置为:加速、爬升、平飞和90°转弯.航迹如图1所示.
图1 三维航迹
为了使验证具有代表性,将本文算法与基于经典卡尔曼滤波和线性化模型的SINS/GPS紧组合算法进行对比.经度误差对比如图2所示.由图2可以看出,在载体无机动保持平飞的情况下,以3 000~3 500 s时间段的经度误差为例,如图3所示,GPF和KF两种算法的位置稳态估计精度相近.但在载体有机动的情况下,以图4所示的2 500~2 700 s转弯机动为例,从图中可以看出,GPF滤波稳定性要明显高于KF滤波.

图2 经度误差对比
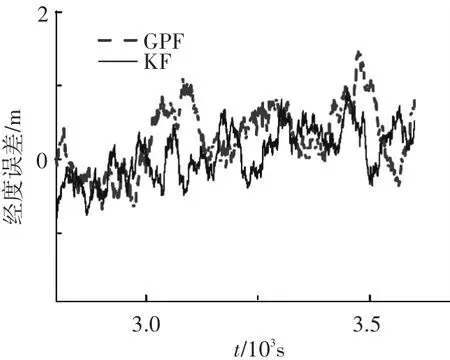
图3 平飞时的经度误差
速度对比以北向速度为例,北向速度全局误差及平飞、转弯机动的误差对比如图5~7所示.
由图5和图6可以看出,即使在平飞状态下,GPF的速度稳态估计精度明显优于KF.由图7可知,在转弯机动时,GPF速度稳态估计精度和稳定性明显优于KF,这与式(3)中分析的速度非线性度高的分析相吻合.

图4 转弯机动时的经度误差
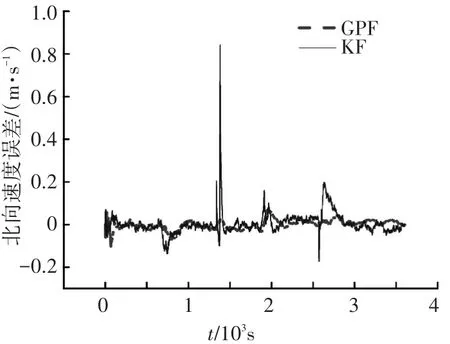
图5 北向速度全局误差
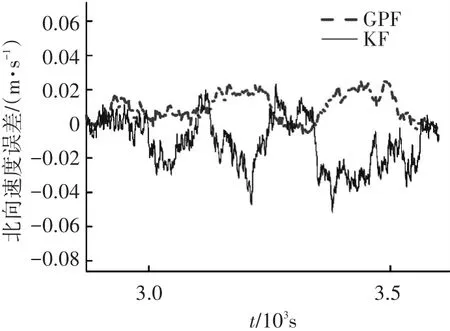
图6 平飞时的北向速度误差
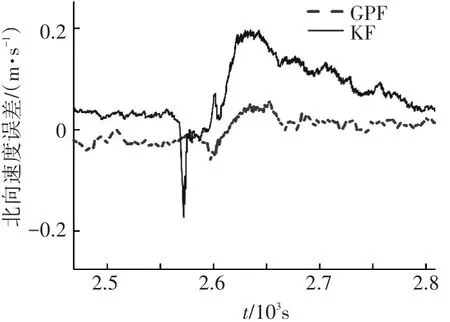
图7 转弯机动时的北向速度误差
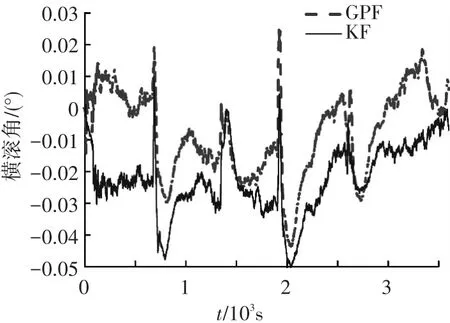
图8 横滚角误差
姿态误差以横滚角为例,其误差如图8所示.
从图8可以看出,GPF的姿态精度略优于KF,但相对速度和位置精度的改善程度,其精度改善不明显,这主要是由于伪距、伪距率组合时姿态不是直接观测量.
表1给出了两种算法的误差对比.仿真环境为Thinkpad T440 i5-2.6 GHz CPU,4 G内存,Matlab2013a 64位版本.
由表1可以看出,本文的算法姿态精度提高了约20%,定位精度提高一倍.同时在本文的仿真环境下,以一次KF的滤波时间作为1个基准时间,本文提出的算法耗时1.54个基准时间,时间消耗只增加50%.

表1 UKF和KF紧组合参数误差对比
4 结 语
针对捷联惯导/GPS松组合方式可靠性和抗干扰能力较差的缺点,本文针对紧组合系统的特点,推导了基于伪距、伪距率的紧组合非线性滤波模型,提出了一种基于线性非线性结构分解的高斯粒子滤波算法.改进算法将系统状态方程分解为线性和非线性两部分,对线性系统部分采用线性KF滤波,对非线性系统部分采用高斯粒子滤波,在时间增加50%的情况下,相比基于KF的紧组合算法定位精度提高一倍.本文提出的方法对SINS/GPS紧组合系统的研究和应用具有重要的理论和实际参考价值.
[1]REN Xiaolu,WANG Changhong,YI Guoxing.Ducted fan UAV hovering attitude control[C]//2011 International Conference on Electronic&Mechanical Engineering and Information Technology.Harbin:[s.n.],2011,1:421-424.
[2]李远伟,奚伯齐,伊国兴,等.小型涵道式无人机的研究进展[J].哈尔滨工业大学学报,2010,42(5):700-704.
[3]OHANIAN O J,GELHAUSEN P A,INMAN D J.Nondimensional modeling of ducted-fan aerodynamics [J].Journal of Aircraft,2012,49(1):126-140.
[4]FARHAD Samadzadegan,GHASEM Abdi.Autonomous navigation of unmanned aerial vehicles based on multisensor data fusion[C]//20th Iranian Conference on Electrical Engineering.Canada:[s.n.],2012:868-873.
[5]于永军,刘建业,熊智,等.非同步量测特性的惯性/星光/卫星组合算法研究[J].仪器仪表学报,2011,12 (3):2761-2767.
[6]de MARINA H G,PEREDA F J,GIRON-SIERRA J M.UAV attitude estimation using unscented Kalman filter and TRIAD[J].IEEE Trans.Ind.Electron.,2012,59 (11):4465-4474.
[7]张海,常艳红,车欢.基于GPS/INS不同测量特性的自适应卡尔曼滤波算法[J].中国惯性技术学报,2010,18(6):696-701.
[8]KONDO S,KUBO N,YASUDA A.Evaluation of the pseudo range performance by using software GPS receiver[J].Journal of Global Positioning System,2005 (4):215-222.
[9]李荣冰,刘建业,赖际舟,等.Sigma-Point直接式卡尔曼滤波惯性组合导航算法[J].控制与决策,2009,24 (7):1018-1022.
[10]ALI J,MIRZA MRUB.Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution[J].Nonlinear Dynamics,2010,61(3):491-502.
[11]熊剑,魏林生,郭杭,等.基于加性四元数的 SINS/ CNS非线性紧组合方法[J].中国惯性技术学报,2012,20(5):596-600.
[12]LIM Jaechan,HONG Daehyoung.Gaussian particle filtering approach for carrier frequency offset estimation in OFDM systems[J].IEEE Signal Processing Letters,2013,20(4):367-370.
[13]段苛苛,李邓化.粒子滤波在光纤陀螺四位置寻北中的应用研究[J].仪器仪表学报,2013,34(8):1749-1755.
[14]刘建业,熊剑,赖际舟,等.采用粒子滤波的捷联惯导非线性快速初始对准算法[J].中国惯性技术学报,2010,18(15):527-532.
[15]周翟和,刘建业,赖际舟,等.一种新的改进高斯粒子滤波算法及其在SINS/GPS深组合导航系统中的应用[J].控制与决策,2011,26(1):85-88.
[16]文志强,朱艳辉,彭召意.粒子滤波目标跟踪中的有效粒子数控制方法[J].控制与决策,2013,28(9): 1349-1360.
[17]于春娣,丁勇,李伟,等.一种基于改进重采样的粒子滤波算法[J].计算机应用与软件,2013,30(2):296-299.
[18]周翟和,刘建业,赖际舟,等.Rao-Blackwellized粒子滤波在SINS/GPS深组合导航系统中的应用研究[J].宇航学报,2009(2):515-520.
[19]刘建业,曾庆化,赵伟,等.导航系统理论与应用[M].西安:西北工业大学出版社,2010.
(编辑 张 宏)
SINS/GPS tightly integrated algorithm with gaussian particle filter
YU Yongjun1,XU Jinfa1,XIONG Zhi2,ZHANG Liang1
(1.Science and Technology on Rotorcraft Aeromechanics Laboratory(Nanjing University of Aeronautics and Astronautics),210016 Nanjing,China;2.Navigation Research Center,Nanjing University of Aeronautics and Astronautics,210016 Nanjing,China)
To improve the reliability of integrated navigation,a tightly coupling nonlinear model based on pseudo range and rate is proposed for reducing the estimation error of tradi-tional algorithm using linear measurement model in this work.For the application of particle filtering to SINS/GPS tightly integrated navigation system,the dimension of the state variables has been a major constraint for the Real-time system.In this new arithmetic,a linear KF deduction and nonlinear GPF method have been employed for the linear part and the non-linear part to improve the precision and real time performance,respectively.Results from the simulation show that the hybrid algorithm can effectively improve the performance of the integrated navigation system,and the precision increases one time.
inertial navigation;integrated navigation;tightly coupling;non-linear filter;gaussian particle filter
V249.3
A
0367-6234(2015)05-0081-05
10.11918/j.issn.0367-6234.2015.05.014
2014-05-19.
中国博士后科学基金(2013M541668);江苏高校优势学科建设工程资助;江苏省博士后基金(1401041B).
于永军(1982—),男,博士后;
徐锦法(1963—),男,教授,博士生导师;
熊 智(1976—),男,研究员,博士生导师.
徐锦法,xjfae@nuaa.edu.cn.

