“数形结合”助力小学数学解题能力的提高

孙凤英

摘 要：随着新课改的深入，数形结合成为重要的数学思想方法之一。使之成为学习数学、解决数学问题的工具，是我们数学教学追求的目标。

关键词：小学数学 数形结合 有效利用 提高效益

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2015）07B-0077-01

数形结合在小学数学教学过程中一直是热门的技巧及教学方向，通过数形结合，可以帮助学生更好地理解数学教学内容，让学生有更扎实的基础面对未来的学习生活。本文就数形结合在小学数学中的有效利用做了探析，希望对广大教育工作者有所帮助。

一、数形结合，有效发展数感

数形结合，是有效培养学生数感的方法之一，数是抽象的数学知识，形是具体的实物、图形、模型、学具。数和形是紧密联系的。学生只有先从形的方面进行形象思维，通过观察、操作、进行比较、分析在感性材料的基础上进行抽象，才能获得数的知识。所以在低年级的数学课堂教学中，数形结合是常用的手段之一。它有利于学生看到物体就能联想到数。用数来表示物体的个数。例如在教学《1000以内数的认识》时，教师便请学生汇报课前是如何数出100根小棒的？学生汇报先是1根1根的数出10根捆成一捆，再10根10根的数出十捆就是100根，学生借助“形”很快知道10个十是一百。教师继续问学生：“你们数100根小棒花了多少时间？”孩子们有的说花了5分钟，有的说花了10分钟……教师微笑表示理解后便要求小组四个同学把小棒合起来数数是多少根，学生们张口便喊出是400根，教师惊讶地问：“数100根小棒都要花5～6分钟的时间，而400根，你们却一下子就数出来啦，怎么数的？”学生们争着说：“我们是100根100根地数。”从而认识了计数单位“百”，紧接着教师课件演示100根100根地数小棒，当数到10个百时，教师追问：这是几个百，10个百是多少？由此引出计数单位“千”，使学生知道10个百就是一千。在教学中教师借助小棒直观形象地将“数”与“形”进行有机结合帮助学生理解数的概念，在数小棒的过程中培养了学生的数感。

二、数形结合，巧妙突破难点

数轴将数有规律、有方向地排列，将数与点建立一一对应关系，将抽象的数形象直观地表示出来，能帮助学生理解数的意义、顺序和大小。如，让学生理解“一个数精确到十分位后是1.0，小数点后的这个0不能去掉”是一个难点。有的教师不厌其烦地强调：“1和1.0的大小相等，但它们的精确度不一样，这个0不能去掉。”有的教师强调说：“如果把0去掉，就不是精确到十分位，而是精确到个位了。”在这样的再三强调下，学生虽然记住了结论，但印象不深刻。某教师出示线段图（如下图）：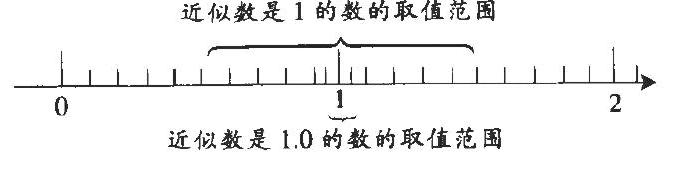

讲解：“约等于1的两位小数取值范围可以是0.5～1.5之间的任何数，而约等于1.0的小数取值范围是0.95～1.05之间的任何数。”从数轴上，学生能够直观地感受到：近似数1对应的准确数取值范围更广，而近似数1.0对应的准确数的取值范围窄多了。小数点后有没有零，对应的范围不一样，因此小数点后的零不能随意去掉。

数轴在数的认识、数的大小比较、数的联系、寻找规律等内容的教学中都可发挥重要作用。如，利用数轴帮助学生理解负数的意义，比较数的大小：利用数轴上的同一个点，让学生认识到“不同的数”——分数（包括不同分数单位的分数）、小数能表示相同的数值。利用数轴，让学生寻找数与数之间的联系。这些既有利于突破教学重难点，又能发展学生的数感。

三、数形结合，剖析数量关系

线段图形是理解数量关系的形象化、视觉化的工具，既能舍弃问题的具体细节，又能形象地揭示条件与条件、条件与问题的关系，把数转化为形，显示出已知与未知的内在联系，激活学生的思维，帮助学生选择合适的解决方法。如：“某月，甲、乙、丙三个同学集邮。已知甲比乙多集了6张邮票，丙集的是甲的2倍，比乙多22张邮票，他们一共集了多少张邮票？”从题目上看，这道题叙述繁杂，让逻辑思维较弱的学生无从下手。某老师引导学生画出线段图（如下）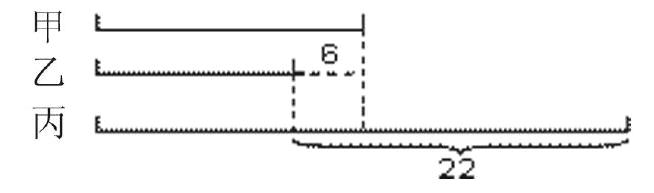

借助线段图，学生发现：22-6 =16，可得甲集了16张邮票：16-6=10，可得乙集了10张邮票；16×2=32，丙集了32张邮票；16+10+32=58，一共集了58张邮票。甚至还有学生发现：“从图上看，三个人集邮总数其实就比4个16少6，求集邮总数可以列式为（22-6）×4-6=58。”线段图的运用、数与形的结合，充分展现了量与量之间的联系，不仅发展了学生的形象思维，而且实现了形象思维与抽象思维的互补。

在小学数学教学过程中，数字和形状的紧密联系不仅能够实现抽象和直观的转化，通过多元化和有效的数形结合的教学模式，也能锻炼小学生将直观图形抽象成数字的能力。

参考文献：

[1]郭进奎.数形结合思想在解题中的应用[J].广西教育，2013，（27）.

[2]李良，张婷.例说数形结合思想在小学数学教学中的应用[J].小学教学参考，2014，（9）.