双曲线问题的几个易错点

甘淑清

（江西省宜春市万载中学）

其实，在求任何一类圆锥曲线方程的时候，我们都要遵循以上方法，先定型就是要求我们根据圆锥曲线的定义，判断出曲线类型是椭圆还是双曲线，或者是抛物线，特别在双曲线的定义中，

在三类圆锥曲线当中，双曲线的问题是最复杂，也是变化最灵活的。双曲线的问题，要求我们在解题时，密切注意双曲线的一些易错点。就可化难为简，以下几个问题，就是双曲线问题中需要时刻注意的。

一、求双曲线方程的步骤：先定型，再定位，后定量

其实，在求任何一类圆锥曲线方程的时候，我们都要遵循以上方法，先定型就是要求我们根据圆锥曲线的定义，判断出曲线类型是椭圆还是双曲线，或者是抛物线，特别在双曲线的定义中，

例1.已知⊙A∶x2+（y-2）2=4，动圆N 恒过定点B（0，-2）且恒与⊙A 相外切，求动圆心N 的轨迹方程。

解：根据题意，可知，圆心距=R+r

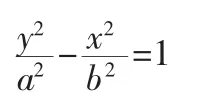
有定义得到2a=2，2c=4 故b2=3

（注：本题初学者在解题时容易犯两个错误，一为判断焦点位置，不少同学总是习惯于设出焦点在x 轴的双曲线，导致方程形式的错误，二为需要注意本题得到的并不是整条双曲线，而只是它的一支，需画出草图，以便正确地取舍。）

二、双曲线的第二定义的准确理解

双曲线的第二定义为：平面内到定点F 距离与到定直线l 的距离之比为常数e-（e＞1）的点的轨迹为双曲线。关于第二定义，教材并未特别强调顶点F 不在定直线l 上的限制，其实这个限制相当有必要，否则其轨迹为两条直线（除定点F）。

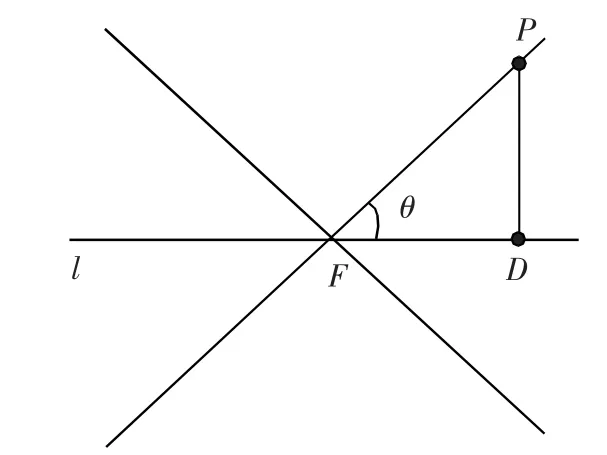
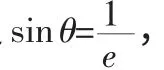
A.椭圆 B.双曲线 C.抛物线 D.两条直线

三、最短焦点弦问题

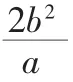
四、焦半径公式的使用

和椭圆一样，双曲线焦半径公式也是由第二定义推倒得出的，但双曲线的焦半径公式有较多的情况分类，因此，运用焦半径公式之前，一定要分清直线与双曲线是交于左支还是右支，或者两支各有一个交点，正确地使用焦半径公式最为重要。

解：（本题不少同学未考虑直线与双曲线的位置关系，误以为直线与双曲线两个交点均在左支，在求AB 弦长时就会错误地用焦半径表达，最终无法得到正确答案。）

双曲线问题虽然形式多样，变化灵活，要准确地把握其知识内容，还是要从基本定义入手，理解定义，做到“咬文嚼字”，另外结合图形特点，遇到直线与其交点的问题，一定要根据与渐近线进行斜率比较，以确定交点位置。很多看似疑难的易错问题就可以迎刃而解。