导引学生“预学”策略浅说

张华

【摘要】 预学是教师有规划地设计学生的自主学习行为，便于进入课堂活动后，教学目标能够更好地得到落实，学生能够有更多的机会寻求解决数学疑惑. 本文阐述了教师前置策略、学生跟进策略等操作思想.

【关键词】 预学；导引；前置；跟进

新课程标准指出，“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上. ”我们在带领学生学习新知识之前应该倡导“预学”，进而“以学定教”，使学生真正做“数学学习的主人”.

但是“预学”不是完全放任让学生在无政府状态下的自发活动，而是纳入教学体系，体现数学学科思想的科学活动. 因此，导引学生“预学”在实施过程中应当讲究策略.

一、教师前置策略

严格来说，学生的“预学”其实属于教学体系中的一个基础性起步环节，它必须经过教师的规范指导，才能充分发挥它的教学价值. 因此，“预学”首先“强调教师的预案设计，教师要认真研究教材，结合课标，把握好每一节课的教学目的、难点、重点，结合学生实际情况，设计出由浅入深、由易到难的预习问题”，这样才能使“预学”高效推进.

二、学生跟进策略

教师的教学宏观架构要落到实处，还必须首先由学生扎实地预学完成. 为此，我们应当用教育智慧驱动学生预学的积极性、培养预学的良好习惯.

1. 目标策略. 即设置明确、科学的教学目标，把控预学的方向，引领学生有的放矢的展开自主学习活动的策略. 根据课程标准，关于平行四边形的学习目标是“探索并掌握平行四边形的有关性质（平行四边形的对边相等、对角相等、对角线互相平分）和四边形是平行四边形的条件（一组对边平行且相等，或两组对边分别相等，或对角线互相平分的四边形是平行四边形）”. 据此，设计出预学目标：

（1）理解什么是平行四边形，提炼出平行四边形的性质，学会用数学符号表示，并能口述出来；（2）初步学会运用平行四边形的性质，尝试独立解答“例题1”“练习”.

学生从这个目标中会接受到这样的信息：（1）掌握什么，即平行四边形的概念、性质；（2）怎样掌握，即用数学符号表示并口述，也就是体现出知识与技能、过程与方法、情感态度和价值观的三维教学目标. 该设计具有科学明确、可操作性两大特点，学生有了这个目标，就可以有针对性地展开预学. 因此，提出目标的语言表达必须简洁明了，具体可见，具有较强的方向性和操作性，不能过于笼统、抽象化.

2. 演习策略. 即根据对教材的阅读，跟随教材对数学知识的解说、论证的推进流程，自主参照演习，再自行比对，排除难点，发现问题的策略. 也就是把教材视为演习的蓝本，不急于直接从教材中寻求结果或者求证过程，而是与教材同步自主尝试推测可能结果或者给出求证的过程.

请看下面的预学设计：

（1）看到课题“平行四边形”时，你想到了 .

（2）读到“你还能举出一些例子吗”时，你想到了 等实物.

（3）从这些例子中说出平行四边形的定义为 ；平行四边形ABCD用数学符号表示应记为 .

（4）看到课题“18.1平行四边形的性质”时，你认为它有 等.

（5）按照“探究”（包括云状图形内的问题）回答，并且动手展开证明.

（6）根据例题，先自主推演.

（7）看到“两条平行线之间的距离”时，你认为它有

等特点，用数学符号怎样表示？

（8）尝试演算“练习”.

该设计充分设置前置问题，让学生先于“答案”积极思考、推演. 这样在和教材给定的“答案”的比对中获得发现的快乐，培养探索精神和数学思维，濡染数学思想，学生就能及时发现预学瓶颈，为下一步参与课堂活动做准备. 可见，提出演习蓝本，让学生阅读教材，探索数学奥妙，能够增强学生的好奇心，调动预学的积极性和趣味性. 久而久之，他们就养成了良好的猜想、验证、排难的习惯，也就逐渐形成了预学能力. 3. 补缺策略. 即在预学过程中，发现与新知识关联的旧知识被遗忘、存在理解障碍等情况时，及时复习、破解的策略. 采取这种策略主要是为了排除新知识学习的障碍. 正如捷克教育家夸美纽斯所说：“一切后教的知识都要根据先教的知识. 理解新知识需要旧知识作基础，预习可以使学生发现旧的知识结构中的薄弱环节，在上课前迅速补上这部分知识，为听课扫清障碍. ”

本课关于平行四边形概念的学习牵涉到小学时候已经接触到的“平行四边形的定义”及“两组对边平行且相等”的性质，论证时牵涉到全等三角形、点与点之间的距离、点到直线的距离等数学概念. 这对于很多学生而言不存在难点，但是对于基础知识薄弱的学生来说，就有必要再温习一下.

另外，在教学设计过程中，我们还应当预设可能存在的重点、难点，采取恰当的方法，帮助学生在预学阶段尝试突破和破解，弥补教材资源之不足. 比如：

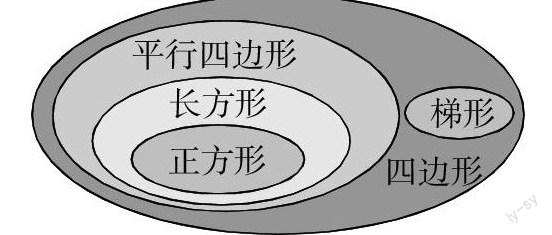
（1）请用直观的形式说明平行四边形与其他四边形之间的关系. 你是否同意下面的标示，为什么？

（2）用图钉把一根平放在？荀ABCD上的细纸板条固定在对角线AC、BD的交点O处. 拨动纸板条，使它随意停留在任意的位置. 观察几次拨动的结果，你有什么新发现？记录下来，再与同伴交流.

（3）已知：？荀ABCD的周长为60 cm，两邻边AB，BC的长比为3 ∶ 2，求AB和BC的长度.

设计（1）（2）是为了帮助学生更好地理解平行四边形的概念及性质，并加强学生的数学体验，获得更深刻的认知，针对本课的教学重点而设计；（3）具有一定的综合性、复杂性，是为了帮助学生更好地运用知识，针对课时的教学难点而设计.

当然，评价策略也应该属于预学策略的一个构成部分，这需要构建評价平台，进入课堂活动.