“平行四边形面积”教学设计

许兰贞

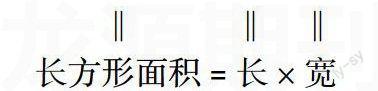
【教学内容】

人教版小学数学教材五年级上册第87～88页例1及相关练习。

【教学目标】

1.经历探索平行四边形面积的计算方法，理解应用“转化”的数学思想方法，推导平行四边形的面积计算公式，会计算平行四边形的面积。

2.让学生经历观察、操作、讨论、分析、比较、归纳等学习活动过程，获得积极的数学学习体验，从而发展学生的空间观念，提高学生的数学素养。

【教学重点、难点】

应用“转化”的思想方法，探究平行四边形的面积计算公式。充分理解剪拼成的长方形与原平行四边形之间的关系。

【教学准备】

平行四边形纸片（多种，各种各样）、尺子、剪刀、课件。

【教学过程】

一、设疑导入

1.课件出示两个图形，这两个图形哪个面积大？引起学生思考。会求哪一个图形的面积？（长方形：长6分米，宽4分米；平行四边形：底6分米，邻边5分米，高4分米。）

预设生：长方形。6×4=24（平方分米）

2.平行四边形的面积呢？今天我们就来探究如何求平行四边形的面积。

板书课题：平行四边形面积

二、探究新知

（一）合理猜想

根据平行四边形提供的数据，先猜测一下平行四边形的面积。

可能出现情况板书：

猜测：1.6×5=30（平方分米）邻边×邻边

2.6×4=24（平方分米）底×高

（二）验证猜想

1.个例研究

（1）我们在学习长方形面积时，通过数面积单位的方法推导出计算公式，现在求平行四边形面积能用这种方法吗？观察一下，这里有不是整个的怎么办？

（2）学生独立思考，操作学具纸。学生汇报交流方法，展示不同方法（2～3个学生说2～3种方法）

可能出现的情况预设：小格左右移动，小格上下移动，沿高剪下大三角形平移合成长方形，沿两个高剪下三角形合并。

思考：形状变了，面积变了吗？

（3）小结：哪种猜想是正确的？转化成长方形就可以用长方形面积公式计算的，长是6分米，宽是4分米，6×4=24平方分米。（底×高6×4=24（平方分米） √）

通过学习我们不但把不够一整格的转化成整格，还把平行四边形转化成长方形直接计算出面积，这个过程运用了转化的方法。

板书：转化

2.多例验证

带着格子的平行四边形可以转化成长方形来计算面积，那你手中的平行四边形能不能也转化成长方形计算面积呢？大家动手试一试，并量出数据、计算出面积。

（1）独立操作，多例验证

放手让学生操作，剪、拼各种不同的平行四边形，完成的同桌交流，能不能？怎么转化的？

（2）展示：转化成长方形了吗？怎样保证转化成长方形？请同学们评价一下。

预设：第1种：一个不沿高剪的图形。让学生明白沿斜线剪拼不成长方形。

第2种：沿高剪的图形。让学生明白沿高剪才能出现直角，拼成长方形。

追问，只能沿这一条高剪吗？

（3）教师引导小结

通过观察、操作（课件演示剪拼）我们发现：不同的平行四边形沿高剪、拼都能转化成长方形，转化前后因为面积没变，长×宽来计算面积。

（三）推导平行四边形的面积公式

1.设疑：如果计算不能剪拼的平行四边形花坛的面积怎么办？能不能也像长方形一样直接用自己的公式来计算？我们再来看看转化前的平行四边形和转化后的长方形，除了面积相等以外，还有什么联系？

2.学生用手中的图形找关系，并把自己的发现与同桌交流。

3.交流总结公式：因为长方形的长就是平行四边形的底，宽就是平行四边形的高，所以长×宽就是底×高。所以平行四边形的面积=底×高。

（课件演示关系完成板书）

平行四边形面积 = 底 × 高

‖ ‖ ‖

长方形面积 = 长 × 宽

4.如果S代表面积，a代表底，h代表高，那么平行四边形面积公式用字母怎么表示？S=ah

【设计意图】通过观察对比，让学生发现转化前后图形之间的相同点之后，沟通两个图形之间的内在联系，借助板书，清晰地推导出平行四边形面积公式。

三、巩固应用新知

1.解决例1：平行四边形花坛的底是6米，高是4米，它的面积是多少？

2.求平行四边形面积。图略。（底12厘米，高8厘米，邻边9厘米）

（1）为什么不能写成9×8呢？（2）为什么不能写成9×12呢？

四、总结

通过这节课的学习，你有什么收获？

五、板书设计

编辑 孙玲娟