高校自主招生试题质量评价标准探索

刘云飞 张亚权 沈 群 薛海彦 于天禾

1 引言

高校自主招生考试，现阶段对社会和教育具有广泛的影响，越来越受考生、家长以及社会各界的关注，而对自主招生试题的质量分析相对较少。目前，对试卷或者试题进行质量分析，主要基于教育测量学和教育统计学的基本原理，根据经典测量理论计算出一系列的指标，这里常用指标包含难度、区分度、鉴别指数、分数分布等[1]。本文以2014年某大学Q类自主招生的数学试卷数据统计分析为基础，从实证的角度出发，分析基于数据的自主招生试题质量。

2 试题的质量评价标准

2.1 学科水平总体描述

我们对参加2014年该大学Q类自主招生的239名考生数据进行了统计分析，如表1所示。本文中，得分率可以表示试题的难度系数，选拔性测验的难度系数最好接近录取率；试题的区分度采用相关系数法计算，即考生在该题的得分与该科目测验得分的相关系数；鉴别指数则采用占考生总人数27%的高、低分组的得分率之差[2]。

由表1可见，2014年该大学Q类自主招生考生数学满分为150分，考生最高分为122分，平均分为75.05分，得分率为50.03%。2014年该大学Q类自主招生考生数学试卷的区分度达到0.47，说明该年数学试卷能够较好地区分考生水平。

表1 2014年该大学Q类自主招生数学成绩数据分析

表2是2014年该大学Q类自主招生数学成绩各个分数段的人数分布表，我们将数学成绩分成四个分数段分别进行统计，结果显示：优秀，数学成绩在110分（含110分）以上的考生比率仅占3.77%；良好，95～109分的占12.13%；合格，80～94分的占25.10%；低分，低于80分的占59.00%。

根据表2所列的数学成绩数据分布情况，以数学“得分”为横坐标，以该得分“人数”为纵坐标，绘制出2014年该大学Q类自主招生考生的“数学成绩分布曲线”，如图1所示。均值75.05分，中数75.00分，众数84.00分，偏度为-0.13，峰度为-0.03，考生的数学成绩总体上接近于正态分布，处于平均分右侧的考生略多于左侧。

2.2 考生水平对比分析

首先按2014年该大学Q类自主招生数学成绩由高到低排序，再根据考生人数平均分成G1、G2、G3、G4、G5和G6六组，然后分别统计各组考生的平均分、标准差和区分度等指标，并作对比分析。

如表3所示，Q类自主招生考生中，高分端（G1）考生的平均分为103.40分，低分端（G6）考生的平均分为45.18分，两极端组的平均分差距为58.22分；G1组至G6组，标准差呈现先依次递减后逐渐递增趋势，G4组的标准差最小，为2.24，说明高分端和低分端的考生成绩分布较离散，而中间段的考生成绩分布较集中，也符合考生成绩正态分布的特点，即在平均分附近有较多的学生分布；两个极端组G1和G6的标准差和区分度都比较大，说明这两组考生的数学成绩差异较为明显，与考生总分的相关性也更强，有利于优秀考生的筛选；G2和G3两组的区分度较大，标准差却均小于3，说明这两组考生的数学成绩与其总分相关度比较高，但成绩分布较集中，差异不明显；G4和G5两组的区分度均低于0.2，标准差偏小，考生成绩比较接近，区分度较差。

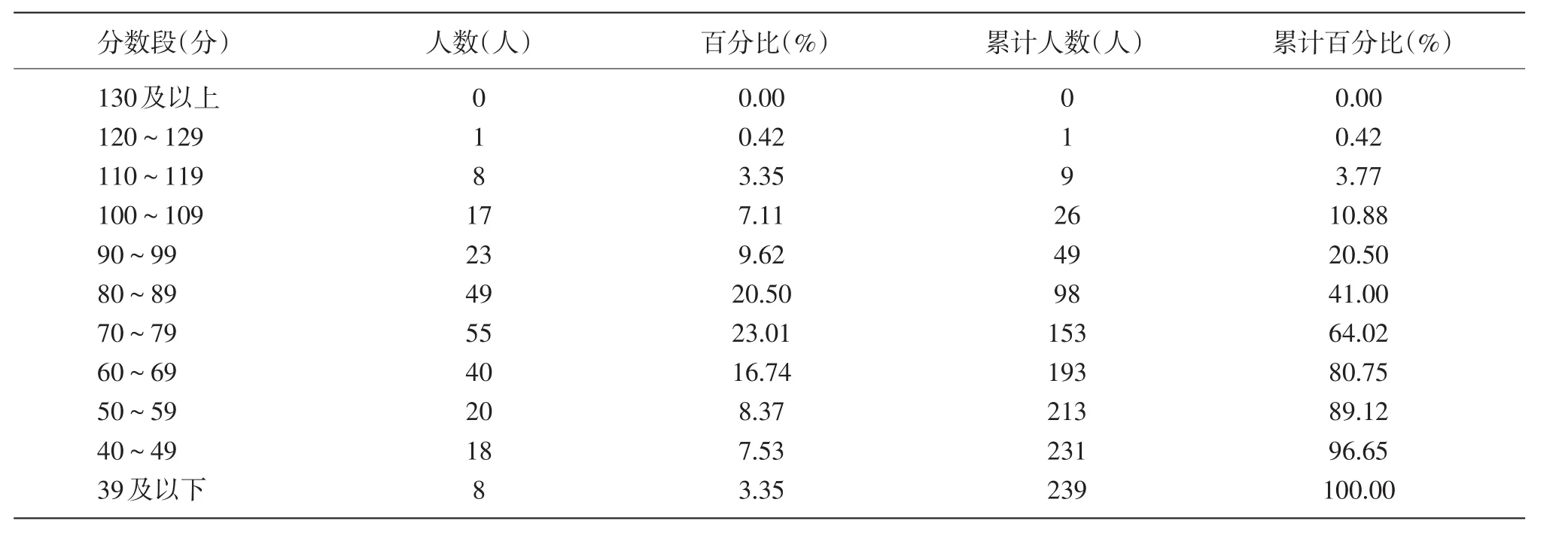
表2 2014年该大学Q类自主招生数学成绩人数分布

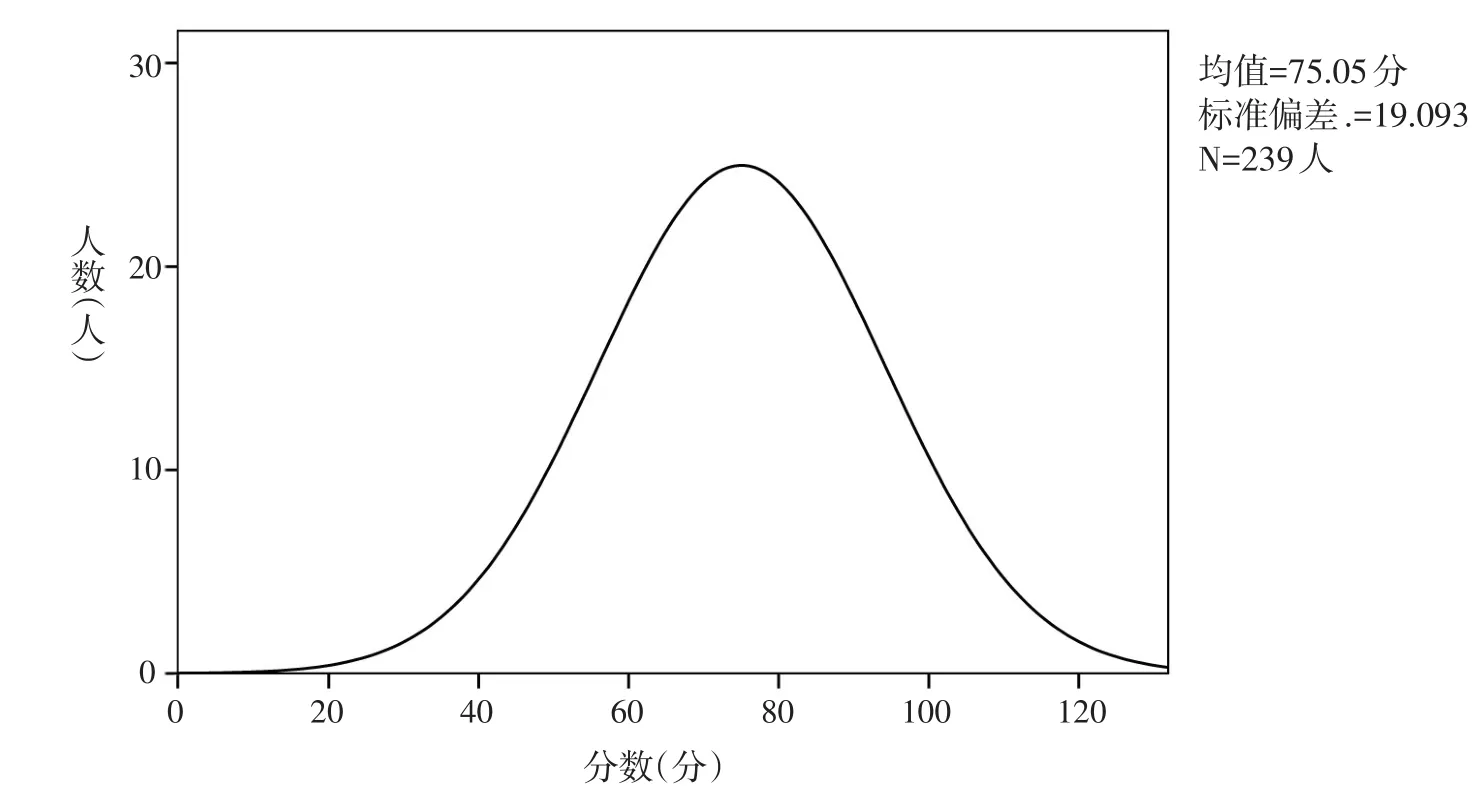
图1 2014年该大学Q类自主招生数学成绩人数分布

2.3 试题解答水平分析

对于选拔性考试来说，试题的难度和区分度是最重要的功能指标。对于难、中、易试题的具体度量标准没有清晰定义，在各种标准中，0.50被作为一个重要基线，将考试的难度或得分率设置在0.50左右时，试卷的区分能力最大[3]。只有当试题的难度范围与考生的能力范围大致相当的情况下，考试才能真正考查出考生的实际水平。

如表4所示，2014年该大学Q类自主招生数学试卷中难题（难度系数0.3以下）有12、14两道解答题，占总分值的26.67%；其余均为中等题（难度系数0.30～0.69），占总分值的73.33%；值得注意的是，全部试题无难度系数大于0.7的容易题，这也符合录取率较低的2014年该大学Q类自主招生考试的要求，这点与高考不同，无须考虑多个不同的目标群体和多个分界点，选拔性的自主招生考试更多关注高分目标群体的区分度，评价自主招生试卷质量应基于试卷能否有效区分目标群体与其他群体。

区分度计算采用相关法，即把某个小题得分与试卷总分的相关系数作为该题的区分度[4]。分析结果显示，区分度大于0.4的优秀试题有填空题和解答第11、13题，占总分的73.33%；区分度良好的试题（0.30～0.39）有解答第14题，占13.33%；区分度较差的（0.2～0.29）有解答第12题，占13.33%；无区分度在0.2以下，需要淘汰的试题。

3 对试题质量评价标准的进一步讨论

以表4中区分度最低的解答第12题为例，得分率仅0.15，试题难度很大，如果仅从难度系数和区分度来分析，这道试题在普通考试中应定位于勉强可用、需修改[5]，但在本来难度较大、通过率较低的选拔性自主招生考试中，这道试题的可用性还需进一步分析。因为自主招生考试有其特殊的目标群体，这时评价试题是不能看一个整体性的难度指标，而应更多考虑试题的目标群体得分率，以及考虑试题能否明显区分目标群体与其他群体[4]。

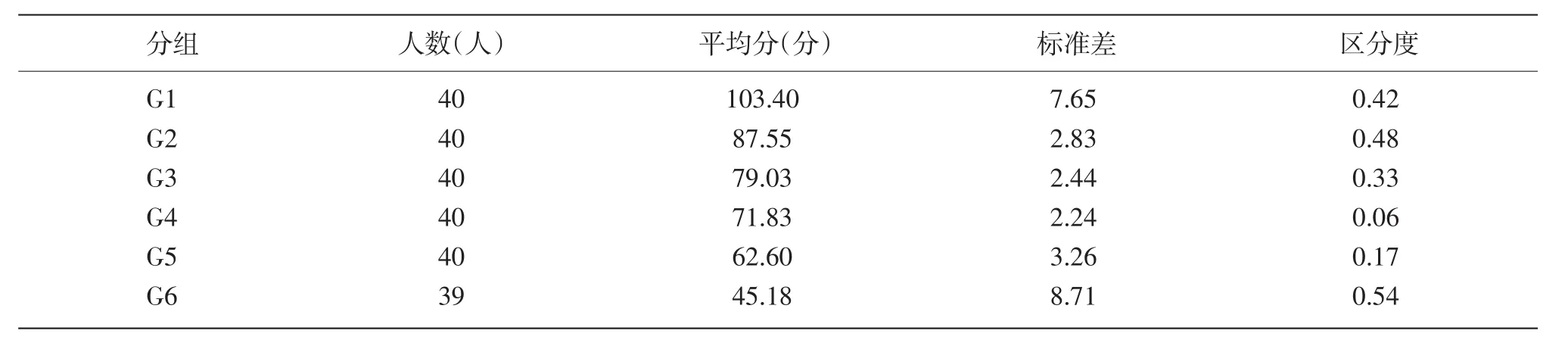
表3 2014年该大学Q类自主招生数学成绩分组对比分析

表4 2014年该大学Q类自主招生数学试题分析

按上面的分组方法，分成G1、G2、G3、G4、G5和G6六组，分析各组在各试题上的得分率差，如果相邻两组的得分率差较大，则说明该试题对这两组群体区分性良好，反之，则区分性较差。从表5中的数据可以看出，G1～G6组在各题上的得分率大致呈依次递减趋势，并且在不同试题上的得分率差别较大。各组在选择题上的得分率变化较均衡，说明选择题对整体考生的区分作用都较好；表4中解答题（11）区分度0.47，鉴别指数0.59，指标都非常高，对考生的区分应该非常好，但从表5中看出，所有相邻两组得分率差中，G1与G2组、G5与G6组得分率差比较大，说明该题对能有效区分高分端G1组和低分端G6组，而对其他组区分较弱；再看解答题（12）得分率0.15，区分度0.27，按数值看显然该题过难，区分度也不够理想，该题应该淘汰，但从表5可以看出，该题在区分低分端和中间分段时不理想，但G1与G2组得分率差值却不小，还是能有效的区分高分端G1组，说明该题作为自主招生考试试题还是可用的；表4中解答题（14）的得分率只有0.15，难度非常大，仅从试卷质量评价整体指数看，该题质量较低，但表5中该题G1组和G2组的得分率差高达0.22，是所有试题中相邻两组得分率差最大的，说明该题能非常有效的区分目标群体G1组与其他组，有利于选拔自主招生中的优秀学生，非常适合作低通过率自主招生的试题。

以上例子说明。区分度和鉴别指数这两个指标可能更说明试题区分的全貌，但对于局部的目标群体的说明不是很有力，这一点在试题难度较大时表现的尤为明显。对于自主招生这种选拔性考试，很多时候命题者关注的不是对全局的区分，而是会适当提高试题的难度，关注对高分目标群体的区分，换言之，关注试题对高分群体的鉴别能力，使得目标群体能脱颖而出。

总之，在实际分析试题的区分能力时，不仅要看其区分度和鉴别指数等整体的数值，还要根据其目标群体得分率差来判断其是否对目标群体产生了良好的区分。当自主招生试题难度较大时，这种分析尤为重要，通过目标群体得分率差的分析也使得对试题的适用性定位更为准确。

4 结语

对自主招生试题的质量评价，区分度和鉴别指数等可作为整体指标来评价试题的质量，同时要考虑到自主招生与普通高考的区别，可以按分数把考生划分为多个群体，根据目标群体和其他群体的得分率差，从而分析试题是否能有效区分目标群体。目标群体得分率差分析要比整体指标更能揭示自主招生试题的本质特征，目标群体得分率差与整体指标结合使用，才能比较客观全面地评价自主招生试题的科学性和适用性。

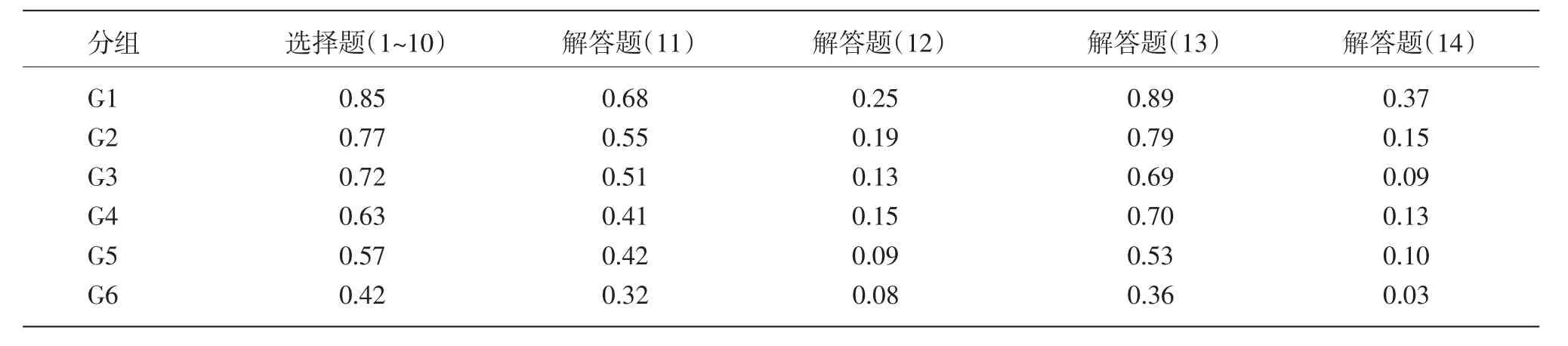
表5 2014年该大学Q类自主招生数学试题分组得分率

[1] 张警麟，郑启跃.考试研究的新课题:对考试的评价[J].教育科学研究，2005（12）.

[2] 湖南省教育考试院高考评价课题组.2013年湖南省高考数学学科（理科）考生水平评价及教学建议[J].教育测量与评价，2013（11）.

[3] 岳伟.高考试卷难度的设计与控制[J].考试研究，2007，3（4）.

[4] 赵海燕，臧铁军.CTT框架下基于数据分析的高考实体质量评价标准[J].中国考试，2009（8）.

[5] 牛学敏.相关系数在试卷质量分析中的应用[J].考试研究，2007,3（4）.