非参数高斯核平滑法估计能力值的精度

张军

1 问题的提出

单维项目反应理论在刻画被试潜在能力与作答反应间的关系时，根据理论模型是否含参数，划分为两类：参数型项目反应理论（Parametric Item Response Theory，PIRT）和非参数型项目反应理论（Nonparametric Item Response Theory，NIRT）。前者不仅要求数据满足单维性、单调性、局部独立性三个假设外，还要求数据拟合逻辑斯蒂函数或正态密度函数等，模型包含1个或多个参数，因此PIRT对数据的约束更多，对题目参数和被试能力参数的估计都需要较大样本，方法更复杂；后者只要求数据满足单维性、单调性、局部独立性三个假设，并不假设数据拟合某种特定函数，模型不含参数。因此与PIRT相比，NIRT更灵活、更容易被理解和接受，更适于描写人格测验等小样本数据[1][2][3]。

运用单维NIRT项目反应理论估计被试潜在能力时，需要根据数据本身的特性，估计潜在能力与答对概率间的对应关系，刻画项目特征反应曲线（ICC）。NIRT的ICC不具备某种特殊形态，如PIRT中ICC的“S”形等。Ramsay[4]提出用非参数高斯核平滑法平滑估计ICC，模拟研究表明这种方法估计时间快速，速度是LOGIST和BILOG两款软件的500～1000倍；而且能充分利用数据本身的特点，有效地估计被试能力并刻画ICC[5]。目前，这种方法的介绍与运用在国内尚属少见，而且此方法在题目数（题量）、被试样本数等不同测验条件下的适用性尚未进行过具体考察。

2 非参数高斯核平滑估计法

假设有N个被试，J个题目，题目有M个选项。被试的潜在能力值为θa，a=1,…,N。yjma为被试a选择题目j中选项m的指示变量，当被试a选择题目j中的选项m时，yjma取值为1，反之为0。被试a选择题目 j中选项m的概率是Pjm(θa)，在非参数高斯核平滑估计法中，通过平滑处理被试潜在能力θa与题目作答反应的关系进行估计。在高斯核平滑估计前，应进行如下步骤：

1.排序。被试按某统计量取值由小到大排序，统计量通常采用被试总分；

2.赋值。按标准正态分布规律，计算被试的百分位数，并将其百分位数作为被试潜在能力值θa的值，a=1,…,N。

3.整理。按θa取值大小给全体被试的作答反应形式进行整理排序，如第a个被试的反应形式为（xa1,xa2,…,xaj）。

对自变量θa与因变量Pjm(θa)进行平滑处理，就是根据二者之间的对应关系，构拟出一条平滑曲线。被试潜在能力值一般从-3到3，在这一区间取若干个值θq作为估计点，比如以0.1为步长，取-3，-2.9，-2.8，……，2.9，3这61个值为估计点。 θa可能与θq重合，也可能不同。通过公式（1）估计每个估计点θq的Pjm(θq)，构拟出一条平滑曲线。

平滑估计的关键原则是局部平均（local averaging），Pjm(θq)是以 θq为中心，以h为宽度的某一范围中所有θa所对应的yjma的加权平均数。在理论上，θa越接近 θq，θa所对应的 yjma与 Pjm(θq)关系越密切，权重waq越大，反之权重越小。计算权重时，使用高斯核函数K(u ) =e(-u2/2),其中 u=(θa-θq)/h 。因此，

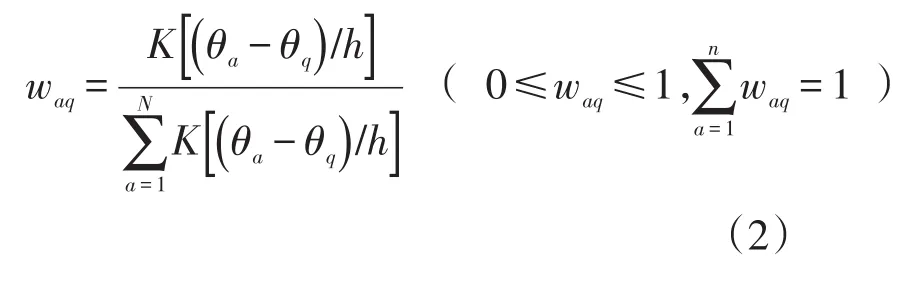
设定宽度h时，不宜过宽或过窄，过宽导致范围内θq过多，直接影响精度；过窄导致范围内θq过少，以致误差过大。一般设定h=1.1N-0.2。

3 实验研究

为检测非参数高斯核平滑法在不同题量、不同样本数条件下，估计被试能力值的精确性设计本实验。

3.1 目的

实验希望解决三个问题：（1）非参数高斯核平滑法是否适用于估计小样本被试的能力值；（2）题量和样本数两个因素对这种方法的估计精度是否存在显著影响；（3）如果题量、样本数对这种方法有显著影响，那么两者应满足何种条件才能保证或达到相应的估计精度。

3.2 设计

由于真实的测验数据难以严格满足实验控制要求，实验使用软件WinGen3[6]，采用蒙特卡罗方法模拟若干套拟合双参数逻辑斯蒂克模型的二分（0/1）项目反应数据，然后使用Testgraf98[7]，运用非参数高斯核平滑法估计被试能力值，估计程序中设定了61个估计点，h=1.1N-0.2。最后，实验比较分析模拟被试的能力值与估计值之间的一致性与偏差。

本实验为6×7设计，含题量和样本数两个因素，题量因素分6个水平，每个水平分别含20、50、100、150、200、250个题；样本数分7个水平，每个水平分别含200、500、1000、2000、3000、4000、5000个被试。潜在能力一般服从正态分布，实验模拟了7个被试群体，均为单维能力，分布为Θ（均值=0，标准差=1）。在项目反应理论中，难度参数与能力参数处于同一量纲中，所以实验模拟了6种题量的难度分度都是B（0,1），区分度处于0到2之间，服从均匀分布。实验共模拟42套数据，具体见表1。

3.3 结果与分析

被试群体的模拟能力值是判定非参数高斯核平滑法估计精度的唯一标准。判定的指标有两个：（1）模拟能力值与估计值两组数据的皮尔逊相关系数，系数越大，两者的一致性越强；（2）两组数据之差的绝对值的平均数B平均，公式为B平均越大说明两组数据间的总体偏差越大。42组数据的相关系数及B平均，分别见表2、表3。

表2、表3数据表明：在某种样本数条件下，随着题量的增加，模拟能力值与估计值的相关逐渐增大，如第2行从左至右，相关系数从0.86增至0.99；而且模拟能力值与估计值之间的偏差越来越小，如第2行从左至右，B平均从0.38缩减至0.12。因此，使用非参数高斯核平滑法估计被试能力值，题量越大，估计的精度越高。当试卷含50个题以上时，可保证能力估计值与模拟值一致程度在0.9以上，平均偏差在0.29以下。如果希望达到一个更良好的精度，如相关系数0.95以上，那么试卷至少应含100个题。

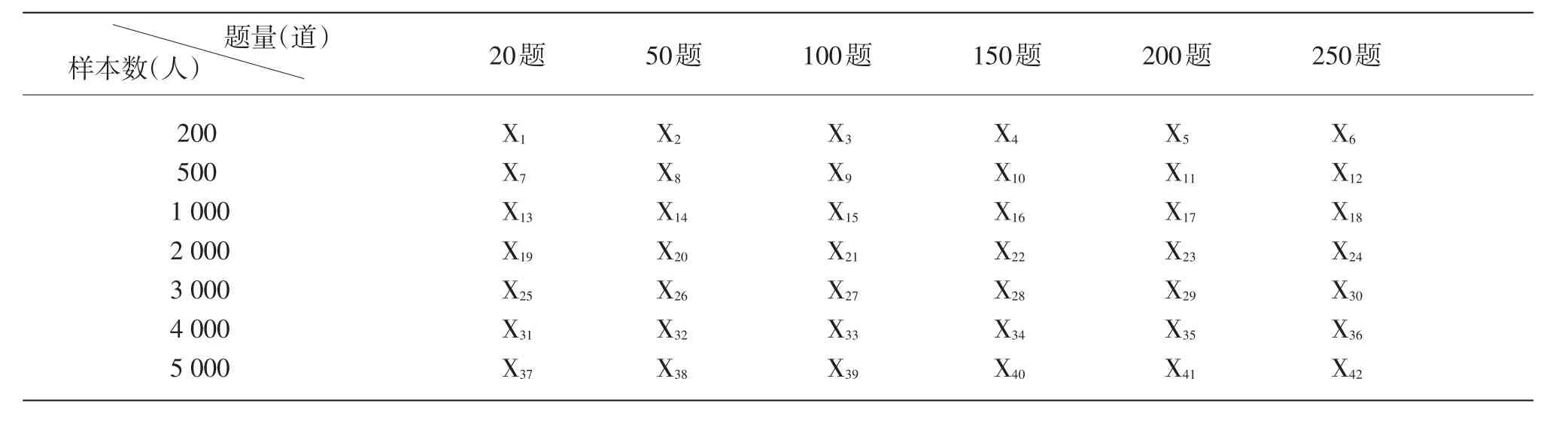
表1 实验设计表

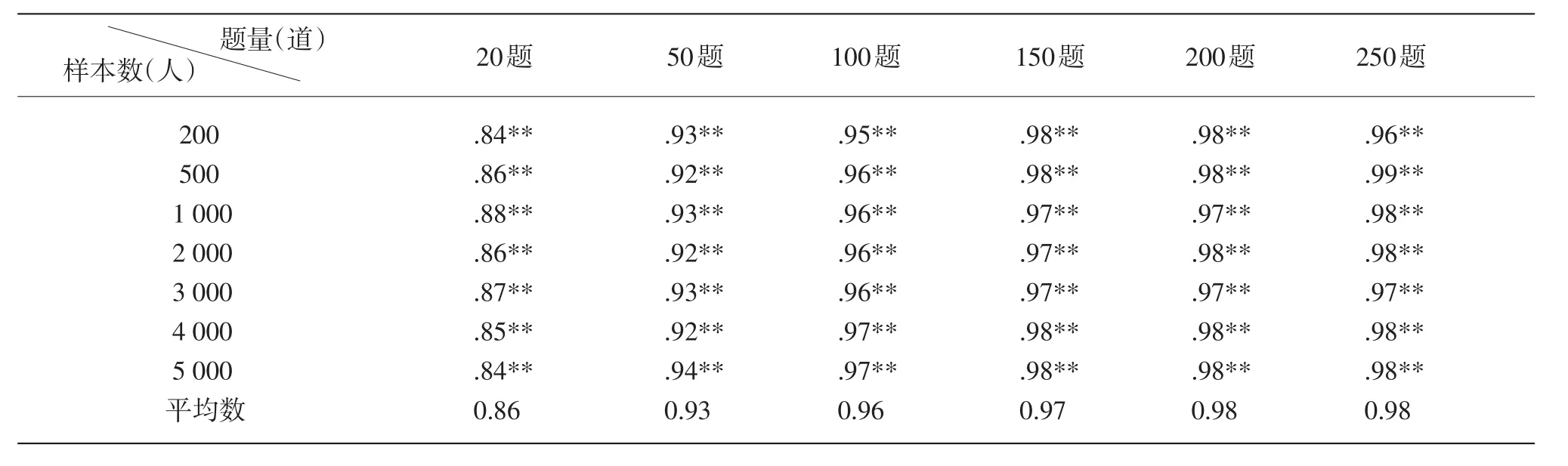
表2 能力估计值与实际值的皮尔逊系数

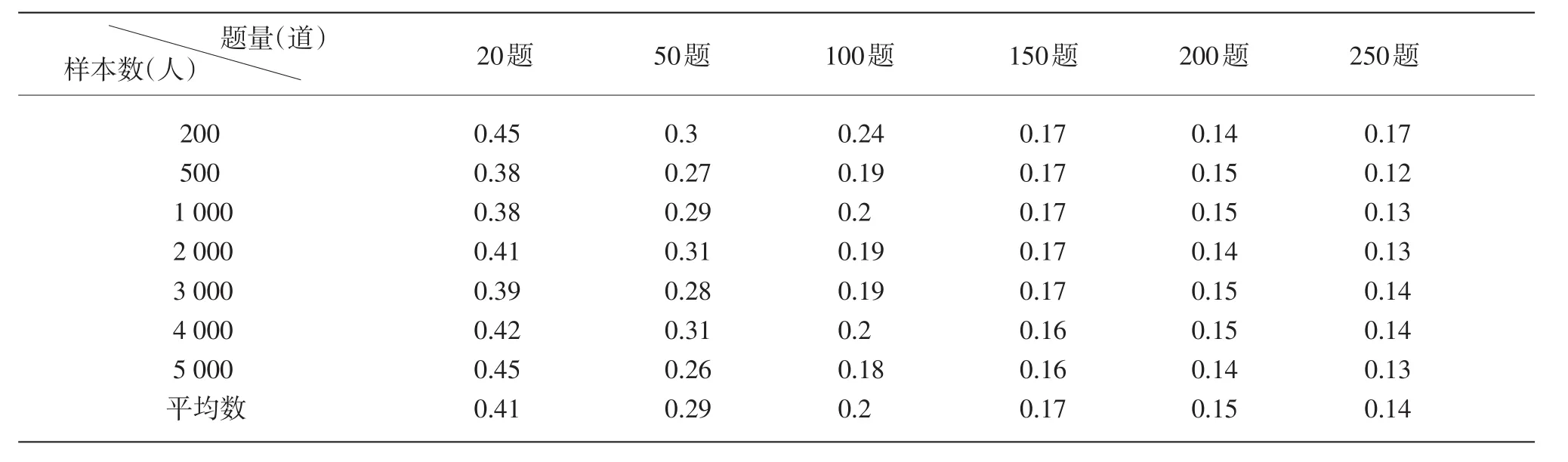
表3 B平均值

另外，在某种题量条件下，样本数的增加对模拟能力值与估计值的相关程度、B平均大小似乎无明显改善趋势，如表2和表3的第1列。为进一步考察样本数和题量两个因素对两组数据间的B平均的影响，实验以表3中的B平均值为因变量，以样本数和题量两个因素为自变量，分别做单因素方差分析，见表4、表5。

样本数因素有7个水平，各水平间的F值为.055，P=.999，组间差异不显著，被试样本数的增加，并未显著改善非参数高斯核平滑法对能力值得估计精度。换言之，被试样本数对估计精度没有影响。由此可知，非参数高斯平滑法不仅适用于估计大样本被试，同样也适用于小样本被试。

题量因素有6个水平，6个水平间的F值为240.478，组间差异在.01水平下显著，这说明题量的大小对估计精度有显著影响。经方差齐次性检验，Levene 统计量为3.905，P=.006＞.5，方差不齐，因此使用Tamhane法对题量不同水平间进行多重比较。表6中第1列中1～6依次代表20题、50题、100题、150题、200题和250题6个水平。

从表6可知，题量为100和150时（水平3和水平4），两种条件下的模拟能力值与估计值的B平均无显著差别，即估计精度无显著改善；题量为200和250时（水平5和水平6）同理。除此之外，其他水平间偏差大小有显著差异，对估计精度有显著改善。

4 结论

（1）在某种样本数条件下，随着题量的增加，模拟能力值与估计值的相关系数逐渐加大，一致性越来越强；而且估计的偏差越来越小，精度越高。

（2）被试样本数因素的7个水平的B平均的组间差异在统计上不显著，样本数的多寡对估计精度没有影响，非参数和平滑法不仅适用于估计大样本被试，同样也适用于小样本被试。

（3）题量因素的6个水平的B平均的组间差异在统计上显著，题量的增加能较好改善非参数高斯核平滑法对被试潜在能力值的估计精度。

（4）当试卷含50个题以上时，可保证能力估计值与实际值一致程度在0.9以上，平均偏差在0.29以下。如果希望达到一个良好的精度，如相关系数0.95以上，那么试卷至少应含100个题。

（5）题量为100题和150题、200题和250题时，这两对水平间的估计总体偏差无显著差异。因此，当试卷从100题增加至150题时，或者从200题增加到250题时，总体偏差并未缩小，对估计精度没有显著改善。在测验实际中，如果只从估计精度考虑，没有必要把题量从100题增加至150题，或从200题增加到250题。

表4 样本数单因素方差分析

表5 题量单因素方差分析

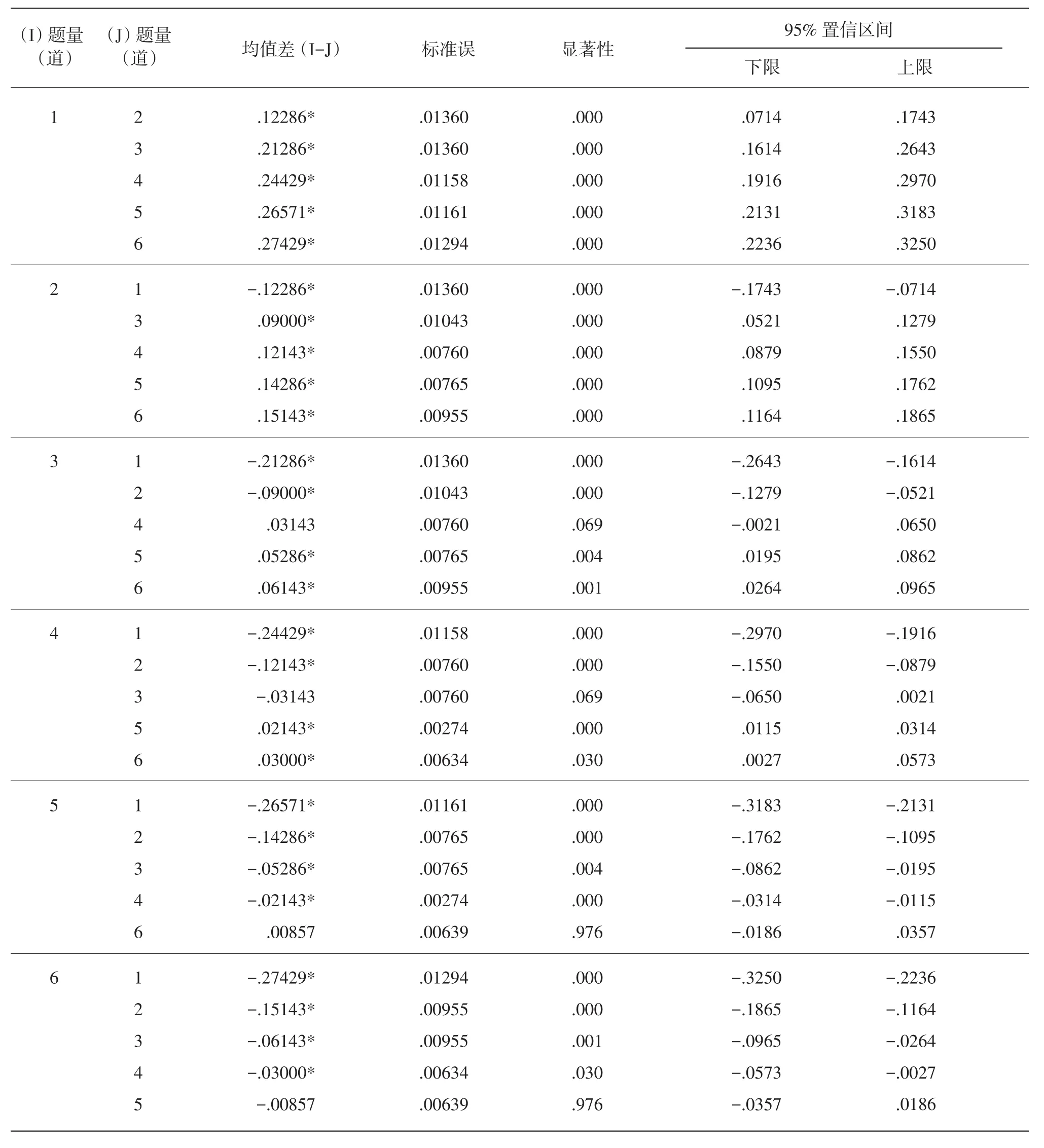
表6 题量因素6个水平间多重比较

[1] Junker,B.W.&Sijtsma,K.，Nonparametric item response theory in action:An overview of the special issue[J].Applied Psychological Measurement，2001.

[2] Meijer,R.R.,&Sijtsma,K.，Methodology review:Evaluating person fit[J].Applied Psychological Measurement，2001.

[3] 张军.非参数项目反应理论在小规模测验中的运用[J].考试研究，2014（1）.

[4] Ramsay,J.O.，Kernel smoothing approaches to nonparametric item characteristic curve estimation[J].Psychometrika，1991（56）：611-630.

[5] Ramsay,J.O.TestGraf:A Program for the Graphical Analysis of Multiple Choice Test and Questionnaire Data[EB/OL].http://www.psych.mcgill.ca/faculty/ramsay/TestGraf.html,2000.

[6] Han,K.T.&Hambleton,R.K.，“Windows Software that Generates IRT Model Parameters and Item Responses”WinGen3[EB/OL].http://www.umass.edu，2007.

[7] J.O.Ramsay，TestGraf[M].McGill University，2000.