谈初中数学教学中函数思想的渗透

胡连成

【摘要】 在新课改的背景下，初中数学课堂教学进行数学思想特别是函数思想的渗透，对于推动课堂教学改革，提高教师素质，培养学生创新能力有着积极的意义，而如何实现这一目的是数学教师应该认真考虑的问题.

【关键词】 数学教学；思想方法；函数思想

日本数学教育家米山国藏在其著作《数学精神、思想和方法》一书的序言中写到：“学生在初中、高中接受的数学知识， 出校门不到一两年，很快就忘掉了，然而，不管他们从事什么业务工作，唯有深深铭刻于头脑中的数学精神，数学的思维方法、研究方法、推理方法和着眼点，却随时随地的发挥作用，使他们受益终生. ”

数学思维蕴含于数学思想之中，数学思想蕴含于数学知识、数学方法和技能技巧之中. 数学思想使数学内容形成统一的和谐. 新的《课程标准》突出强调：“在教学中，应当引导学生在学好概念的基础上掌握数学的规律（包括法则、性质、公式、公理、定理、数学思想和方法）”. 函数是中学数学的重要内容，运用函数思想可以解决很多数学问题. 因此教学中应重视函数思想的渗透.

一、用运动变化观点归纳知识形成体系

许多数学知识表面上是孤立，只要我们从运动变化的观点去观察分析，就不难发现它们的内在联系，从而把零碎的知识变成一个统一的整体，使理解深化.

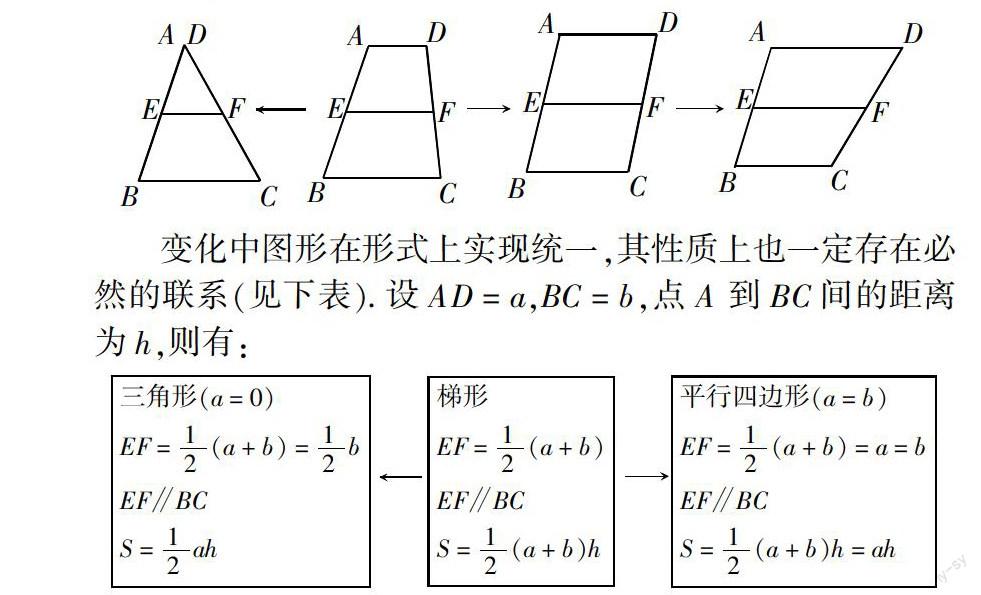
例1 三角形、平行四邊形和梯形（如下图）可以这样理解：当梯形ABCD的顶点D，在直线AD上向左运动至点A时，梯形变为三角形；当点D向右运动时，梯形依次变为平行四边形、梯形.

变化中图形在形式上实现统一，其性质上也一定存在必然的联系（见下表）. 设AD = a，BC = b，点A到BC间的距离为h，则有：

揭示运动变化规律最好的工具就是函数. 人类对函数的认识经历了 “变量说”、 “对应说（映射说）”、 “关系说”三个阶段. 可以说，函数概念的灵魂是运动变化、是变量间的对应关系. 函数思想就是串起知识项链的主线，它不仅是数学研究的对象，也是解决现实问题常用的一种方法. 函数思想广泛地渗透到数学学习的全过程，不仅数轴、有理数与实数的概念和运算、式的运算及恒等变形、方程与不等式等蕴含着函数思想，而且图形的变化、性质之间的关系也和函数思想存在着一定的联系，函数的重要性不言而喻.

二、注重运用函数思想解决问题

在数学解题中，以函数思想为主导，运用函数方法，结合具体函数的性质，可以使很多数学问题转难为易、化繁为简，是一个很重要的解题策略思想，人们统称为函数法.

例2 （14年天津市第12 题）已知二次函数y = ax2 + bx + c（a ≠ 0）的图像如图，且关于x的一元二次方程ax2 + bx + c - m = 0（a ≠ 0）没有实数根，有下列结论：

① b2 - 4ac > 0；② abc < 0；③ m > 2. 其中，正确结论的个数是 （ ）.

A. 0 B. 1 C. 2 D. 3

分析： ①②借助函数图像比较容易解决，③的判断难度较大，要注重方程与函数的联系：

一元二次方程ax2 + bx + c - m = 0没有实数根，则可转化为ax2 + bx + c = m，即可以理解为y = ax2 + bx + c和y = m没有交点，即可求出m的取值范围.

三、运用函数思想进行教学设计

教师采取教学方法、教学程序的有效性取决于是否体现了数学思想方法的灵魂作用，没有数学思想指引的课堂是肤浅的、是不利于学生思维发展的. 对学生未来发展起决定作用的不是掌握知识的多少而是解决实际问题策略选择，蕴含数学思想的教学可以培养学生灵活有效的思考问题、解决问题，潜移默化的影响学生的将来发展. 因此，在数学思想中起着统领作用的函数思想理所当然在数学教学要发挥重要的指导作用.

例3 学习“倒数”时，教师可以从三个层次加以引导.

1. 了解倒数的定义的基础上会求一个非0实数a的倒数.

2. 理解一个非0实数a的倒数仍为实数，感受数a与它的倒数是一对一对应关系.

3. 进一步思考当数a（a > 0）增大时，■将随之减小；当数a（a < 0）规律相同.

教学如果仅停留在第一层次，那就是单纯传授知识的教学，学生只是掌握了倒数的求法，而在思维上没有得到发展. 只有把学生对倒数的理解引导二、三层次，从崭新的角度去理解问题，才能真正培养学生的数学思维能力.

数学知识之间相互联系、相互渗透，从而丰富了人们对问题的认识. 为了培养学生数学学习中的运算能力、逻辑推理能力、空间想象能力及综合运用数学知识解决问题的能力，学生在学习中不但要养成用联系观点归纳知识，还要有意识地运用函数思想方法去解决实际问题. 函数思想是中学数学重要的数学思想，教师教学中注重发挥函数思想的指导作用，让数学知识逐渐内化为学生的数学素质.

【参考文献】

[1]季素月，王力耕，尤善培.给数学教师的101条建议，南京师范大学出版社，2005.9.