一个需要完善的经典反例

☉浙江省桐乡市凤鸣高级中学 沈金兴

一个需要完善的经典反例

☉浙江省桐乡市凤鸣高级中学 沈金兴

一、棱柱定义与经典反例

文1中提到了棱柱概念的进化并提供了一个典型反例，笔者觉得这个反例值得商榷，有必要做进一步完善.

先看一下人教版教材《必修2》1.1.1节中对棱柱下的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱.而作为一线教师，一定会同时给出一个辨析题：能否把棱柱定义为“有两个面互相平行，其余各面都是平行四边形的多面体是棱柱”.

绝大多数同学会认为可以，当然也有一部分同学觉得不可以，但理由会说：“如果可以这样简洁地定义，那教材为何还要这么啰嗦地下定义呢？”这显然不是数学方面的理由，而是逻辑上的理由.其实，要否定它，只要一个反例就可以了，但要让学生自己去独立思考，可能会很难想到.因此，教师就会给出像文1中一样的一个经典反例，如图1.

图1

二、对反例的诘问

首先来看多面体的定义，以人教2004年版教材为例，多面体定义为“由若干个平面多边形围成的空间图形”，并对多面体进行分类，“把一个多面体的任一个面伸展成平面，如果其余的面都位于这个平面的同一侧，这样的多面体叫做凸多面体”，而另一类便是凹多面体.

接着来看图1这个反例，它虽然是辨析题中那个定义的反例，但显然这个反例是凹多面体的.笔者以前在上《棱柱》这节课时，也是举这个经典反例的，可在最近一次上这节课时，有学生一下课就来追问：“老师，棱柱是多面体，而多面体有凹、凸之分，可刚才给出的反例是一个凹多面体，那在凸多面体中有没有反例呢？如果没有，则辨析题那个定义中的多面体只要改成凸多面体不就正确了”.最后该生又加了一句话：“反正老师您给出的这个反例不能让我信服！”

面对学生的诘问，笔者也思索起来，觉得学生说得很有道理.这么说，以前我们举的经典反例是有问题的，那只不过是凹多面体中的一个反例，还缺少凸多面体中的反例.笔者一方面为学生有这样的批判性思维而高兴，另一方面自己也陷入了深思.

三、数学史上的棱柱定义

回头再看一看在数学历史发展过程中对棱柱下的定义.

早在古希腊数学家欧几里得（约公元前330-275）著的《几何原本》中，在其第Ⅺ卷有这样一个定义：“一个棱柱是一个立体图形，它是由一些平面构成的，其中有两个面是相对的、相等的，相似且平行的，其他各面都是平行四边形.”［2］这个定义不就是辨析题中的说法吗？由此可见，棱柱的这种错误定义来源于影响了2000多年的《几何原本》.古希腊先贤也犯了错，难怪现在的学生会重蹈覆辙.这也进一步印证了“历史发生原理”：学生对数学概念的理解过程与数学概念的历史发展过程具有一定的相似性，历史上数学家所遭遇的困难正是学生所经历的障碍.［3］

由于《几何原本》是经典几何中的“圣经”，故没有数学家对棱柱定义提出怀疑，即使到了二十世纪初依旧如此.在1906年，数学家Failor对棱柱重新下了定义：棱柱是两个面为全等且平行的多边形，其他面为平行四边形的多面体.在1913年，数学家Smith也把棱柱定义为：有两个面为平行平面上的全等多边形，其他面均为平行四边形的多面体.显然，这两个定义还是《几何原本》中棱柱定义的翻版，只是描述得简洁一点而已，并无本质区别.这说明该定义的反例是很难找的，否则在历经2000多年的历史长河中，到了上世纪初竟还无一位数学家提出修正，所以学生想不到反例也很正常.

四、完善反例并制作模型

由于平时举的这个反例是属于凹多面体的，故需要再举一个凸多面体的反例，这样才完整.当然，也不必重起炉灶，只要在原有反例的基础上进行完善，把它变成凸多面体就可以了.

1.用“补形”方法来完善

原有的反例是凹的，那只要在凹进去的地方补上一个多面体，使之变成凸的不就行了，当然侧面还是要保证平行四边形的.为了更一般化，原来反例中的上、下底面可改成一般的四边形，然后为了美观，还可再“补形”，使上、下底面为平行四边形，最后就得一个很漂亮的凸多面体反例.具体的“补形”过程见图2.

2.用“切割”方法来制作

凸多面体的反例是在原有凹多面体反例的基础上通过“补形”方法得来的，但在给学生说明时，还不太好办，因为这个反例不容易画.所以，最好能制作一个模型，直接给学生看，这样就很有说服力了.

但要凭空制作这个反例的模型也有点困难，于是就联想到立体几何中常用的“切割”方法.由于反例有十二个面，取上、下相对的两个有四条棱的顶点，则发现该顶点可看成一个四棱锥的顶点，即有4个侧面，这样上下就有8个侧面，再加上中间四个面，就构成十二个面了.如此一来，就很自然地想到正八面体，然后取各条棱的中点，再把各中点相连就形成了图2中的凸多面体反例.具体“切割”过程如图3，最后再旋转一下观看，就诞生了一个完美的凸多面体反例模型，如图4.

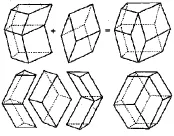
图2

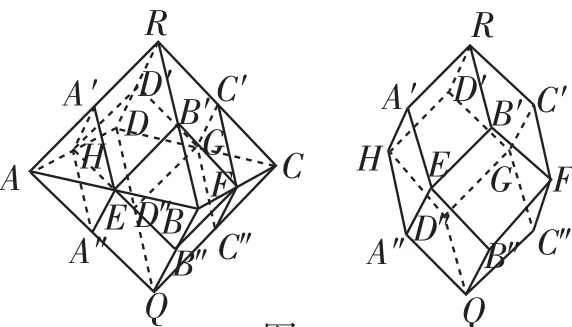
图3

图4

五、结束语

至此，针对棱柱错误定义的反例就完善了，从而让学生更加明白了教材中对棱柱所下定义的正确性.由于流传了2000多年的《几何原本》中对棱柱下的错误定义，从而导致了学生对棱柱定义的误解也属正常，因为历史上这么多大数学家都认为《几何原本》中的棱柱定义是正确的，更何况学生.而教师举的反例也不应只局限于凹多面体的，还要补充凸多面体的反例才完整.希望本文完善的反例能给一线教师在教学上带来方便.

1.冯耀斌.HPM视角下高中数学若干“核心概念”的回归［J］.中学数学（上），2014（3）.

2.欧几里得，箸.几何原本［M］.兰纪正，朱恩宽，译.南京：译林出版社，2011.

3.汪晓勤，韩祥临.中学数学中的数学史［M］.北京：科学出版社，2002.FH