基于数学活动经验的问题解决——一组中考压轴题赏析

☉江苏省南京金陵中学河西分校　李玉荣

基于数学活动经验的问题解决
——一组中考压轴题赏析

☉江苏省南京金陵中学河西分校李玉荣

《数学课程标准（2011年版）》明确指出：“通过义务阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”“几何直观主要是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探究解决问题的思路，预测结果.几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用”.可见，几何直观的培养需从帮助学生养成画图的习惯、学会画图并利用图形思考、想象问题开始，积累数学活动的经验，最终更好地感知数学、领悟数学、解决问题.近几年陕西省的中考压轴题的命制在这方面做了积极、有益的探索，很好地践行了几何直观的理念，值得借鉴与学习.

例1（2009·陕西省）问题探究

（1）请在图1的正方形ABCD内，画出使∠APB=90°的一个点P，并说明理由.

（2）请在图2的正方形ABCD内（含边），画出使∠APB= 60°的所有的点P，并说明理由.

问题解决

（3）如图3，现有一块矩形钢板ABCD，AB=4，BC=3.工人师傅想用它裁出两块全等的、面积最大的△APB和△CP′D钢板，且∠APB=∠CP′D=60°.请你在图3中画出符合要求的点P和P′，并求出△APB的面积（结果保留根号）.

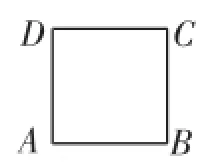
图1

图2

图3

【赏析】命题者以独到的视角，将尺规作图与剪裁钢板的实际应用联系起来，第一、二问的“问题探究”要求画出满足条件的“一个点”和“所有的点”，一方面体现了从“特殊”到“一般”的探究问题的基本策略，另一方面将第二问中所获得的方法迁移到第三问的“问题解决”之中，可以顺利地完成从“一般”到“特殊”应用数学知识解决实际问题的过程，有效地考查了学生应用数学的意识，以及合理利用所学知识建立数学模型、解决实际问题的能力.当确定点P和P′的位置后求△APB的面积，只需利用解直角三角形的知识确定底与高即可.试题的呈现自然、简捷、和谐，具有较好的数学教育价值.

例2（2010·陕西省）问题探究

（1）请你在图4中作一条直线，使它将矩形ABCD分成面积相等的两部分.

（2）如图5，点M是矩形ABCD内一定点，请你在图5中过点M作一条直线，使它将矩形ABCD分成面积相等的两部分.

问题解决

（3）如图6，在平面直角坐标系中，直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图，其中DC∥OB，OB＝6，BC＝4，CD＝4.开发区综合服务管理委员会（其占地面积不计）设在点P（4，2）处.为了方便驻区单位，准备过点P修一条笔直的道路（路的宽度不计），并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分.你认为直线l是否存在？若存在，求出直线l的表达式；若不存在，请说明理由.

图4

图5

图6

【赏析】此题的“问题探究”以作图题呈现，考查等分面积问题，实际上为第三问做好铺垫，解决第三问既要想到将梯形分割成一个矩形和一个三角形，又要借助于几何图形的直观发现点P（4，2）为矩形ABCD的对称中心，将问题转化为直线将三角形面积平分即可，体现了数学转化思想，遗憾的是后续的计算难度较大也很烦琐（有超标嫌疑）.此题所示问题情境中的“问题探究”和“问题解决”，表面上看，似乎是一般的操作，但更深层次地可以理解为另一类的阅读，这种阅读不是显见的文字阅读，而是学生有效整合已经内化的矩形相关知识，通过画直线的操作活动，具有思考性、推理性地阅读题意，并获取相关策略和方法的过程，思维含量层层提升，较好地考查了学生知识结构的完备性和对知识理解的深刻性以及思维的灵活性.

例3（2012·陕西省）如图，正三角形ABC的边长为3+

（1）如图7，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上.在正三角形ABC及其内部，以A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大（不要求写作法）.

（2）求（1）中作出的正方形E′F′P′N′的边长.

（3）如图8，在正三角形ABC中放入正方形DEMN和正方形EFPH，使得D、E、F在边AB上，点P、N分别在边CB、CA上，求这两个正方形面积和的最大值及最小值，并说明理由.

图7

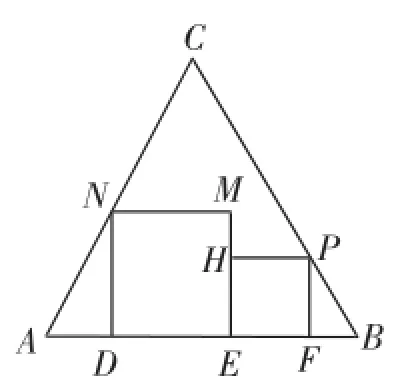
图8

【赏析】此题的第一问是源于课本的一道作图题，第三问提出了求两个正方形面积和的最大值及最小值，可考虑这两个内接正方形的极端位置：当两个正方形的边长相等时，它们面积的和最小，当其中一个正方形的面积最大时，它们面积的和最大，设正方形DEMN、正方形EFPH的边长分别为m、n（m≥n），求得面积和的表达式为：S=+（m-n）2，可见S的大小只与m、n的差有关：①当m=n时，S取得最小值；②当m最大而n最小时，S取得最大值.而m最大n最小的情形就是第一、二问所得结果.试题命制精巧、内涵丰富，集求最大、最小值问题于一个图形，彰显了新课标“由知识立意向能力立意过渡”的教学要求，较好地体现了“源于基础，重在思维”的评价理念，对日常教学具有一定的示范作用.

例4（2013·陕西省）问题探究

（1）请在图9中作出两条直线，使它们将圆面四等分.

（2）如图10，M是正方形ABCD内一定点，请在图10中作出两条直线（要求其中一条直线必须过点M），使它们将正方形ABCD的面积四等分，并说明理由.

问题解决

（3）如图11，在四边形ABCD中，AB∥CD，AB+CD= BC，点P是AD的中点.如果AB=a，CD=b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由.

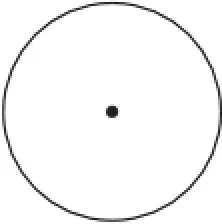
图9

图10

图11

【赏析】此题第一、二问与例3极为相似，是通过作图等分面积，求解过程对第三问的求解有提示作用，但第三问的变式幅度较大：一方面图形从圆、正方形变为梯形，另一方面将“两条直线四等分面积”变为“一条直线两等分面积”，这就需要通过补形来达到目的，联想到条件“AB+CD=BC”，可以补成一个菱形，做到了数学经验活动上的“正迁移”.本题借助几何图形这个对象，以及相应所具有的条件，提出了画直线平分几何图形的任务.本题的“问题情境”可以说是情境设计中的材料，也可以是“问题解决”中应赋予的条件，同时问题中几何图形构成的不断变化，从特殊到一般，能凸显出策略的形成与应用，并体现出不同的认知要求和能力层次，运用解答题型设计试题使探索该问题解决途径的过程逐步得以呈现，并顺应问题中图形从特殊到一般的条件变化，能凸显问题解决中认知要求和能力的层次性.该问题不仅关注了对基础知识与技能的考查，更加关注了对学生数学活动经验的考查.此题所反映出的命题理念与构造策略，值得借鉴与研究，而且对学生转变学习方式具有积极的意义.

例5（2014·陕西省）问题探究

（1）如图12，在矩形ABCD中，AB=3，BC=4.如果BC边上存在点P，使△APD为等腰三角形，那么请画出满足条件的一个等腰△APD，并求出此时BP的长.

（2）如图13，在△ABC中，∠ABC=60°，BC=12，AD是BC边上的高，E、F分别为边AB、AC的中点.当AD=6时，BC边上存在一点Q，使∠EQF=90°，求此时BQ的长.

问题解决

（3）有一山庄，它的平面图为如图14的五边形ABCDE，山庄保卫人员想在线段CD上选一点M安监控装置，用来监视边AB.现只要使∠AMB大约为60°，就可以让监控装置的效果达到最佳.已知∠A=∠E=∠D= 90°，AB=270m，AE=400m，ED=285m，CD=340m.问：在线段CD上是否存在点M，使∠AMB=60°？若存在，请求出符合条件的DM的长；若不存在，请说明理由.

图12

图13

图14

【赏析】第一问，由于△PAD是等腰三角形，底边不定，通过作图发现需分三种情况讨论，再运用勾股定理等知识即可解决问题.第二问要求以EF为直径作⊙O，易证⊙O与BC相切，从而得到符合条件的点Q唯一，然后通过添加辅助线，借助于正方形、特殊角的三角函数值等知识即可求出BQ的长.第三问中要满足∠AMB=60°，可构造以AB为边的等边三角形的外接圆，该圆与线段CD的交点就是满足条件的点，然后借助于等边三角形的性质、特殊角的三角函数值等知识，就可算出符合条件的DM的长.显然，三个问题都需要构造与求解相关的图形才能奏效，“做数学”的意识跃然纸上，考查了操作、探究等能力，综合性非常强.

上述几道中考压轴题独具匠心的设计突出了“做数学”的过程，彰显了过程性教学理念，通过“作图”这样的数学活动积累经验去解决问题，对几何直观的理念做出了很好的诠释.这里的数学活动是在考场而不是在课堂，问题解决不是靠合作交流而是需自主探究，图形有助于发现、描述问题，有助于探索、发现解决问题的思路，基本活动经验的获取直接影响问题解决.在教学中要有意识地强化对基本图形的运用，不断地运用这些基本图形去发现、描述问题，理解、记忆结果，把让学生掌握一些重要的图形作为教学任务，贯穿在义务教育阶段数学教学、学习的始终，使学生积累有效的数学活动经验，不仅在中考中得心应手，对数学的认识和运用的能力更一定终身受益.