别解见证关联常规凸显不凡

☉山东省滨州市北镇中学初中部　邢成云

别解见证关联常规凸显不凡

☉山东省滨州市北镇中学初中部邢成云

一、试题再现

题目：（2014年菏泽市中考题第20题）已知：如图1，正方形ABCD，BM、DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MN．

（1）若正方形的边长为a，求BM· DN的值；

（2）若以BM、DN、MN为三边围成三角形，试猜想三角形的形状并证明你的结论．

图1

二、试题解析

（1）因为BM、DN分别平分正方形的外角，所以∠CBM=∠CDN=45°，所以∠ABM=∠ADN=135°.

因为∠MAN=45°，所以∠BAM+∠NAD=45°．

在△ABM中，∠BAM+∠AMB=180°-135°=45°，

所以∠NAD=∠AMB.

在△ABM和△NDA中，因为∠ABM=∠NDA，∠NAD=∠AMB，所以△ABM≌△NDA．

所以BM·DN=AB·AD=a2.

（2）以BM、DN、MN组成的三角形为直角三角形，证明如下：

如图2，过点A作AN的垂线AF，在该垂线上截取AF=AN，连接BF、FM.（或将△AND绕点A顺时针旋转90°至△ABF的位置，使得AD与AB重合，连接BF、FM，或以AM为对称轴作△AMN的对称图形△AMF，连接BF）

图2

因为∠1+∠BAN=90°，∠3+∠BAN=90°，所以∠1=∠3.

在△ABF和△AND中，因为AB=AD，∠1=∠3，AF= AN，所以△ABF≌△ADN，所以BF=DN，∠FBA=∠NDA= 135°.

因为∠FAN=90°，∠MAN=45°，

所以∠1+∠2=45°=∠FAM=∠MAN.

在△AFM和△ANM中，因为AF=AN，∠FAM=∠MAN，AM=AM，所以△AFM≌△ANM.

所以FM=NM．

所以∠FBP=180°-∠FBA=180°-135°=45°.

所以∠FBP+∠PBM=45°+45°=90°．

所以△FBM为直角三角形.

因为FB=DN，FM=MN，

故以BM、DN、MN为三边的三角形为直角三角形.

说明：若计算出MN2=BM2+DN2，再用勾般定理的逆定理得出该三角形为直角三角形（亦可）.

三、追本探源

以上的中考题应该源于以下题目：

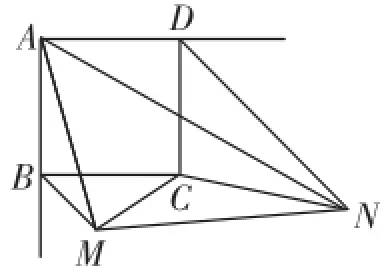
图3

已知：如图3，正方形ABCD的边长为a，BM、DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN.

（1）填空：与△ABM相似的三角形是_______，BM·DN=_______；（用含a的代数式表示）

（2）求∠MCN的度数；

（3）猜想线段BM、DN和MN之间的等量关系并证明你的结论.

命题者对它稍稍进行了改造，粗加工而成：把问题（1）的填空题改编成了一道解答题，内涵一致，确定为新试题的第（1）小题；舍弃了原来的问题（2），把原问题（3）的问题显性化，与三角形的三边挂钩，探索的方向更明确一些，较之原题的难度降了一点.

四、思路分析

试题解析给定的是构造全等三角形的方法，或用旋转变换构图、活用轴对称变换作图等，是对图形变换等全等变换的灵活考查，如此确定答案充分展示了图形变换的不菲作用，但这一辅助线并没那么容易想到，这个好的“念头”难有根基，难以登录学生的思维场域，是对学生较高的思维要求，学生感叹巧的同时，往往流露出一种无奈与无助.其实这道题目有基本的转化思路，常规的很，并且有机链接了题目的两个子问题，使得题目的构思更显现其智能价值，而不至流于拼凑的嫌疑.

五、别样的精彩

仅限于第（2）小题，不难发现BM、DN和MN三条线段可以看做是梯形的两底一腰，只要把BD一连，一个直角梯形就显现在我们面前，剩下的任务无非就是寻找直角梯形两底与一腰的关系，这类问题我们有非常朴素的经验，作梯形的高，通过“勾股定理”把它们链接在一起，然后就是代数变形了.这些想法更接近学生的已有经验，更贴近我们的数学教材，更重要的是这道题目的魅力才能得到更好的展现.

如图4，连接BD，过点M作MH⊥DN，垂足为点H，可证四边形MNDB为直角梯形，进而得知MH=BD.又BD=，DH=MB，根据勾股定理得MN2=MH2+NH2，即MN2=BD2+（DN-BM）2，MN2=（a）2+ DN2+BM2-2DN·BM.根据（1）的结论BM·DN=a2，可知MN2=（a）2+DN2+BM2-2a2，则MN= DN2+BM2.根据勾股定理逆定理可知以BM、DN、MN为三边的三角形是直角三角形.

图4

六、方法比对

方法一（试题解析）：这一方法以图形的全等变换为载体，立足三角形全等的构造，通过全等三角形的性质及相关知识进行推理获得“90°”角，进而作出构成直角三角形的判断，有精妙轻巧之感，但有远离学生的基本经验之嫌.

方法二：另一个思路其实在给定的“标准答案”之后有说明，但不知何因没有给出具体的过程.这个方法，立足图形现有的元素，用最通俗的作梯形高辅助线（小学生都会的辅助线），然后借助勾股定理构建起相关给定三线段的数量关系，借力问题（1）中获得的结论变换而得三线段的平方关系，根据勾股定理逆定理敲定问题的答案.相比之下，这个方法脱胎于学生学习《四边形》一章的基本经验，不高蹈、不玄妙，更贴近学生，更接地气.

若从欣赏的角度来说，这两个方法可以说相得益彰，一个是图形变换、一个是数式变换，纵横两大领域；若从题目本身承载的效能来说，试题解析制定成第二个思路的形式，更能体现题目命制的精妙，因为用第一个思路，第一问就是摆设，两个子问题不搭界，彼此不相往来；若用第二个思路，境界就不同了，第二问有机链接了第一问，呈现内在的“递进”求解关联，使得两个子问题浑然一体，那命题者的良苦用心才会真正体现出它的价值来.

两个方法、两个思路、两重境界.

1.段长荣.“妙解”源于“厌繁”［J］.上海中学数学，2013（10）.

2.单墫.解题研究［M］.南京：南京师范大学出版社，2002.

3.刘瑞祥.从命题视角谈“并列”问题与“递进”求解［J］.中学数学（下），2014（9）.