把握操作契机,促进概念内涵与外延的有效对接
黄丽华


摘 要 概念是反映事物本质属性的思维形式,数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映。每一个数学概念都有其确定的内涵和外延。在数学概念教学中,要重视概念教学的每一个环节,把握操作契机,促进概念内涵与外延的有效对接。
关键词 概念教学 操作 内涵 外延
中图分类号:G622.42 文献标识码:A 文章编号:1002-7661(2015)11-0062-03
数学概念尽管是抽象的,但它反映了现实世界的数量关系和空间形式,只有概念理解了,才能进行有效的数学思维活动和判断、推理,这就需要理解概念的内涵与外延。因此,在数学概念教学中,要重视概念教学的每一个环节,把握操作契机,为学生创设自主、合作、探索的学习机会,提供自主学习、有效思维和积极体验的时间和空间,把学生从单一的书本、封闭的课堂中解放出来,让学校在活动中、操作中轻松地学习,促进概念内涵与外延的有效对接。
【片段一】动手操作,探索发现
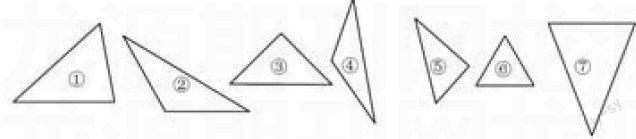
出示7个三角形:
师:这些都是?它们有什么共同的特征?
生1:它们都有三条边,三个顶点,三个角,
生2:它们都是封闭图形,具有稳定性。
生3:……
师:那它们完全一样吗?
生1:它们的角的大小不一样。
生2:它们边的长短也不一样。
师:那你能根据这些不同,按一定的标准给这些三角形分分类吗?请根据要求,倒出信封里的三角形动手分一分。
投影出示合作要求:
小组合作要求:
1.根据一定的标准独立分类。
2.小组内说说你是怎么分的。
【思考】《数学课程标准》指出:“数学学习活动必须建立在学生认知发展水平和已有的知识经验基础之上”,数学课堂教学对有着不同理解能力的学生来说,从他们自己的已有知识和经验出发,总能有一份属于自己的发现和收获。从平时的教学中发现,学生对直角三角形、钝角三角形和锐角三角形都有一个模糊的认识,但不会运用准确地语言进行表达。
依照传统的教学方法是先出示分类学习表格:
根据表格让学生先把三角形的三个角量一量,统计出直角、钝角、锐角的个数,再根据直角、钝角、锐角的个数的特点给三角形按角进行分类。按边分的时候也是先测量每条边的长度,从而得出三条边都相等的三角形是等边三角形和有两条边相等的三角形是等腰三角形。而我在课堂教学中,让学生自己动手操作,比一比,折一折等在学生独立思考的基础上进行小组合作交流让学生的思维由感性认识上升到理性认识。
因此本节课伊始,我直接给每个学生7个具有代表性的三角形:通过让学生动手折一折、量一量、分一分等多种形式的实践操作丰富强化学生的感性认知,让学生的产生认知冲突,以激发学生的探究欲望,从而磨砺思维品质。接着为学生提供了更多探索空间,让学生自主选择分类标准,保证了实验操作结果的代表性和普遍性。在这个自主探究的过程中,学生自己充分地去“玩”三角形,独立去感受每一个三角形的特征,让“三角形”这个概念的内涵与外延在学生的头脑中形成一定的表象。紧接着让学生以小组为单位进行合作交流,当学生通过自己的方式感受到三角形之间的联系和区别时,再进一步提升学生的分析概括能力,进而将三角形进行比较科学的分类。
在课堂教学实践中,大部分学生都能按角进行分类,而且能很清楚的描述每类三角形的特征,并能用三角板上的直角去比一比进行验证。还有的学生能用量一量和对折的方法找到等边三角形和等腰三角形,通过折,发现等腰三角形和等边三角形的对称性,为后续研究埋下伏笔,从而使这两类三角形的概念得到了很好的落实,它们之间的关系更加明确,学生在操作中对概念的内涵与外延也有了深刻的认识。
【片段二】精心设计,讲求实效
出示:猜猜后面藏着谁?
师:你知道后面藏着什么三角形吗?为什么?
生1:第一个是直角三角形,因为有一个角是直角。
生2:第二个是钝角三角形,因为有一个角是钝角。
生3:第三个是锐角三角形,因为有一个角是锐角。
生4:不对,不对第三个三种三角形都有可能。
师:为什么?
生1:因为每种三角形都有锐角。
生2:每个三角形中至少有两个锐角。
课件出示三种三角形。
师:直角三角形和钝角三角形只看一个角就能判断了,那么锐角三角形能不能也看一个角就能确定的呢?
生1:不能。
生2:能看三角形中最大的角,如果最大的角是锐角,那么这个三角形肯定是锐角三角形。
【思考】数学概念尽管是抽象的,只有充分地理解概念的内涵与外延,才能使每种三角形特征地认识从模糊走向清晰。在教学活动中,猜信封下藏着的是什么角,是为了加强学生对直角三角形、钝角三角形、锐角三角形这三类三角形的理解,凸显出本质属性,特别是第三个猜一猜,让学生了解有一个锐角的三角形不一定是锐角三角形,有两个锐角的三角形也不一定是锐角三角形,并在脑中呈现出三角形的形状,突破锐角三角形三个角必须都是锐角这一难点,对三角形概念的外延更加明晰。创设这样一个学习空间,是让学生多角度多方位去思考,从而在加强基础知识教学的同时,又培养学生思维的灵活性。使得整个教学环节既有了广度又有了深度,成为了本节课教学的一个亮点。正所谓真理越辩越明,概念学习就是在不断地辨析中深化、巩固的,同时,概念的内涵与外延得到了进一步的理解。
【片段三】拓展游戏,辨析提升
师:在这个格子图中,如果下面这条黄色的线段是三角形的底,另外一个顶点在与左边端点垂直的位置上,同学们想一想,这是一个什么三角形?
生:直角三角形。
师:你是怎么发现的?
生:因为这两条线互相垂直了。
师:如果这点在这里呢(指在端点的垂线上)?
生:直角三角形。
师:这里呢?
生:直角三角形。
师:想象一下,如果这个点不停的往上往上往上,往下往下往下,这些三角形都是?
生:直角三角形。
师:那么这个点还可能在哪里,也是直角三角形呢?
生:在另一个端点的垂线上。课件展示
师:如果另外一点在这条垂线之外呢?
生:是钝角三角形。
师:为什么?
生:因为这里有一个钝角(生手指着钝角的地方)。
师:如果在这两点之间呢(有意识的移到锐角三角形的地方)?
生:锐角三角形。
师:移到等腰直角三角形的地方,问:这是什么三角形?为什么?
生1:直角三角形,因为有一个角是直角。
生2:如果按边看,它是等腰三角形,因为它有两条边相等。
师:看来这是一个等腰直角三角形。
师:把这个点往上往下移,问:是什么三角形?这个点在哪里,组成的三角形都是等腰三角形?
生:在底边中点的垂线上。课件出示这条线。
师:把点停在等边三角形的位置上,问:这是什么三角形?
生:等边三角形。
师:确定吗?怎么办?
生:用尺子量。(课件进行测量演示)
师:这样的等边三角形还有吗?还有几个?在哪里?
生:在下面还有一个,与上面这个对称的。
【思考】以游戏操作的形式进行练习,提升所学知识,学生兴趣盎然,效果更佳。为了使学生学得愉悦、对知识掌握得更加扎实,我觉得,这个环节的设计是本节课的又一个亮点,在这个活动中教师适当地演示,巧妙的问题引思,层层深入;从直观感知到思维提升,逐步建立每类三角形的空间观念,使每一类三角形的特征在学生的脑海里留下了深刻的印象。在这个精彩的活动过程中,巧妙地沟通了直角三角形、钝角三角形、锐角三角形之间以及等腰三角形与等边三角形的联系,并渗透了极限思想,使每类三角形的内涵和外延进行了有效的对接。由于小学生受年龄特点的限制,他们对形象具体的、数量有限的事物容易理解,对抽象的事物难于掌握。因此,教学中不能忽略极限思想方法的重要性,要充分考虑学生的长远发展及终身发展。本节课中,我利用这个有趣的游戏将极限思想方法进行适度的渗透,让学生在动态的过程中,形成了一个完善、系统的知识网络,使学生记忆犹新。
【片段四】后测比较,凸显成效
课堂后测是检验教学效果的最有效的方法,我对不同教法的两节课都进行了随堂后测,参加本次检测四(3)班47人,四(4)班49人,回收率100%。
学习后测练习:
通过检测,发现学生③④⑧这三个错得最多,但两个班级这三个图形的正确率相差却很大。以下是两个班级的后测对比分析表:
后测对比分析表:
从这一组数据可以看出,采用传统教学方法的四(3)班学生,空间观念没有得到很好的发展,概念内涵掌握得还行,但对概念的外延考虑不全面,理解不深刻,导致概念运用不够灵活,不能全面分析问题。课后对几个做错的学生进行跟踪调查,对于做错的原因,学生是这么回答的:
生1:我的⑦三角形没有连到锐角三角形,我只考虑三条边都相等的是等边三角形。
生2:我是③三角形没有连到等腰三角形,我忽略了每个三角形除了按角分,还可以按边分。
生3:④三角形很明显是一个等腰三角形,由于这个直角直接不好判断,我以为连了一种就好了。
……
【分析】概念的内涵就是这个概念所反映的对象的本质属性的总和,而概念的外延就是适合这个概念的一切对象的范围。从学生的回答中,我们不难发现,对于⑦三角形,学生更多的考虑等边三角形的内涵:三条边都相等的三角形是等边三角形。而它的外延:三个角都是锐角,是一个等角三角形不是很清楚。再如等腰三角形,这一概念的内涵是有且只有两条边长度相同的三角形,其外延则是等腰锐角三角形、等腰钝角三角形、正三角形。由于学生对概念的内涵和外延的理解不明确,模糊,以至于学生每个图形只考虑一种分类标准,忽视了还可以朝其它方面进行分类,概念运用不够灵活,造成四(3)班错误率如此之高。而改进教学方法后,课堂中,我重视让学生通过充分操作过程去自主发现每类三角形的本质属性,以及外延的理性思考,关注内涵与外延的紧密联系,从具体操作到抽象概括,让每类三角形的特征展现得淋漓尽致,学生在操作、体验、感悟中建构了新的知识系统,所有,四(4)班的后测效果比四(3)班有非常明显的提高。
总之,在几何概念教学中,要把握操作契机,提供给学生充分的动手操作的时间和空间,真正地体现《新课标》中所倡导的“自主、合作、探究”的新型学习方式,使学生获得生动活泼的、主动而富有个性的发展,拓宽知识领域,达到概念内涵与外延的有效对接。
参考文献:
[1] 章建跃,陶维林.概念教学必须体现概念的形成过程[J].数学通报,2010,(1).
[2] 宋运来.什么是最有效的教学[M].江苏:江苏人民出版社,2009.

