实对称矩阵应用的两点体现

孙卫卫

（青岛理工大学琴岛学院，山东 青岛 266106）

0 引 言

通过利用实对称矩阵的一些特性可以有效地解决一般的二次曲面［1－3］方程图形的推断与二元以上多元函数极值［1－3］的求解问题。现在就从上述两个角度来阐述实对称矩阵的具体应用。

1 一般的二次曲面方程的图形推断

对于一些简单的二次曲面方程很容易推断其形状，而对于复杂的二次曲面方程推断其形状是比较困难的，例如z＝xy。而实对称矩阵［4－5］的加入，使得这个问题的解决变的容易许多，以下给出实对称矩阵对一般的二次曲面方程图形推断的具体方法。

二次曲面的一般方程［6］

其中，aij，bi，c为实数（i，j＝1，2，3）。

设：

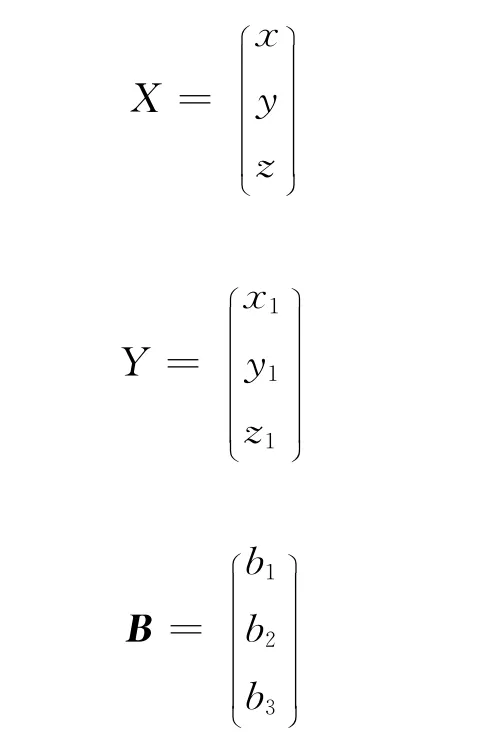
二次曲面可表示为：

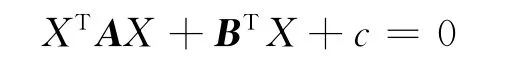
由于A为实对称矩阵，因此存在正交的矩阵P，有：

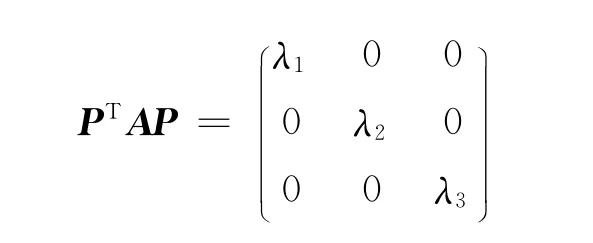
其中，λ1，λ2，λ3为特征值。

由正交变换X＝PY可得：

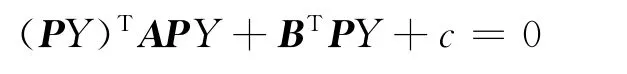
令（d1，d2，d3）＝BTP，整理得：

又因为正交变换具有保持向量内积和长度不变的性质［4－5］，因此可得如下定理：

定理1 方程（1）所表示的曲面形状与方程（2）所表示的曲面形状相同。

定理1正是运用了实对称矩阵在正交矩阵的作用下可以对角化的性质而得到的，所以，如果遇到非标准形式下的二次曲面方程，也可以通过这一性质将其化简，从而推断其图形。下面通过具体例题来实现实对称矩阵的具体运用。

例1：推断下列方程表示怎样的图形：

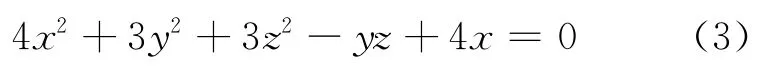
解：得实对称矩阵：

存在：

有：

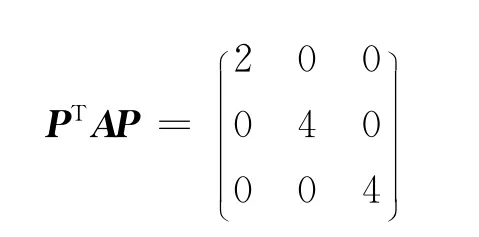
又：

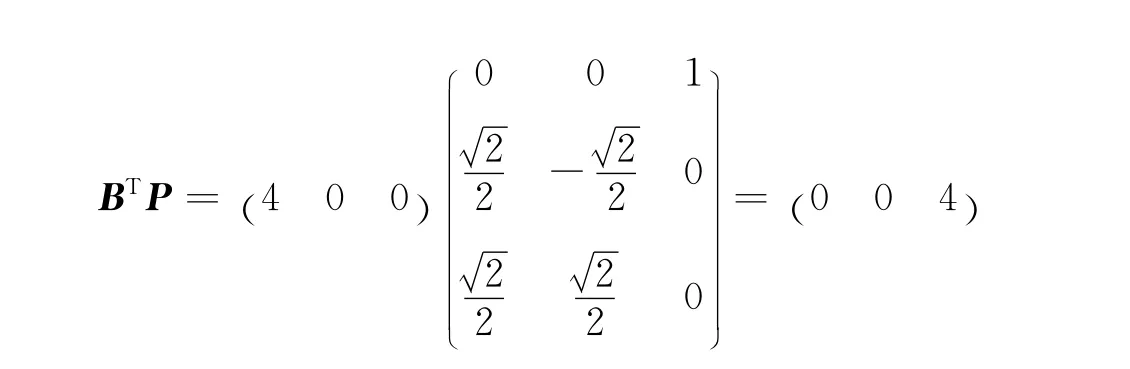
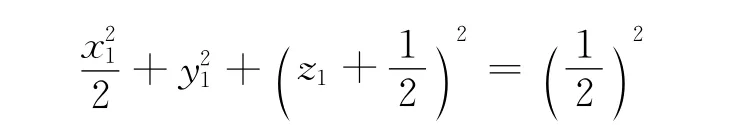
因此式（3）表示椭球面。

2 多元函数极值的求法

二元函数z＝f（x，y）在（x0，y0）的某邻域内连续且具有一阶、二阶连续的偏导数，又

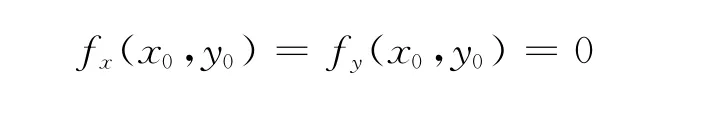
令

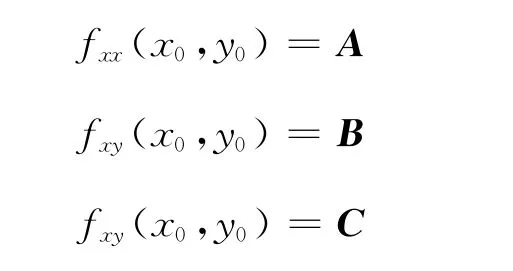
则有：

1）AC－B2＞0，（x0，y0）是极值点，A＞0是极小值点，A＜0是极大值点；

2）AC－B2＜0，（x0，y0）不是极值点；

3）AC－B2＝0，无法判定。

设矩阵

又

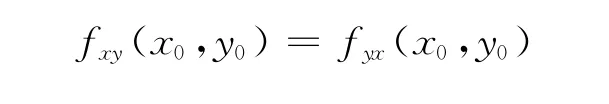
1）D正定，（x0，y0）是极小值点；

2）D负定，（x0，y0）是极大值点；

3）D不定，（x0，y0）不是极值点（这一结论也可由泰勒公式进行证明，详见文献［2－3］）。

将这一结论进行推广：

设：u＝f（P）＝f（x1，x2，…，xn），u＝f（x1，x2，…，xn）在P0（x10，x20，…，xn0）某邻域内连续，并具有一阶、二阶连续的偏导数，又有，由于，2，…，n），因此引入实对称矩阵：

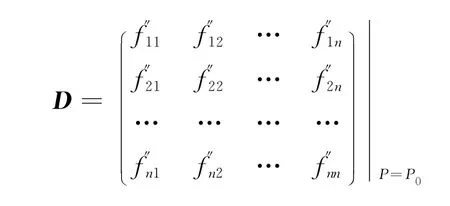
则有结论2：

1）D正定，（x0，y0）是极小值点；

2）D负定，（x0，y0）是极大值点；

3）D不定，（x0，y0）不是极值点（这一结论也可由多元函数的泰勒公式进行证明，详见文献［7］）。

将结论2运用到三元函数，并根据实对称矩阵的正定性与顺序主子式的关系可得如下定理：

定理2 三元函数u＝f（x，y，z）在（x0，y0，z0）的某邻域内连续并具有一阶、二阶连续的偏导数，且fx（x0，y0）＝fy（x0，y0）＝fz（x0，y0）＝0，又二阶混合偏导相等，引入实对称矩阵：

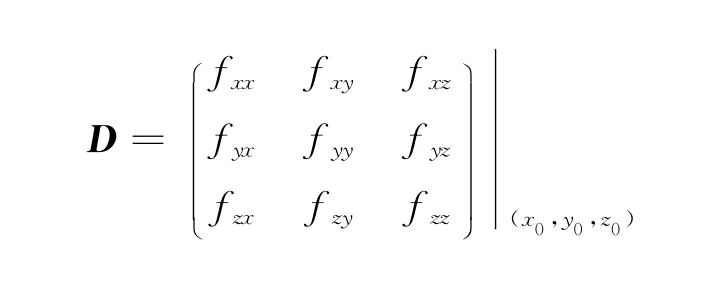
则有如下结论：

1）｜D｜＞0

（x0，y0，z0）为极小值点；

2）｜D｜＜0

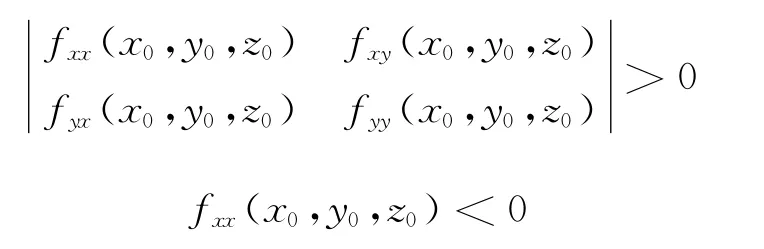
（x0，y0，z0）为极大值点；

3）｜D｜＝0，无法判定；

4）不属于上述3种情况，则不是极值点。

定理2正是运用了实对称矩阵的正定性的判别方法而得到的，所以，如果三元函数的极值点的判定都可以根据｜D｜的顺序主子式来进行准确的分析。

下面通过具体例题来实现这一具体应用。

例2：求f（x，y，z）＝e2x（x＋y2＋2y）＋z3－3z极值。

解：求一阶偏导得：

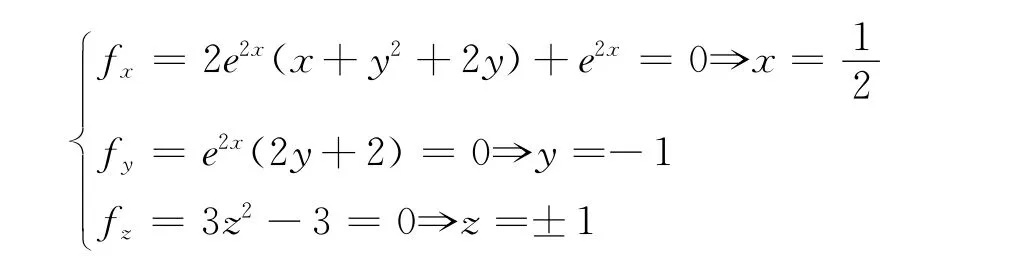
又

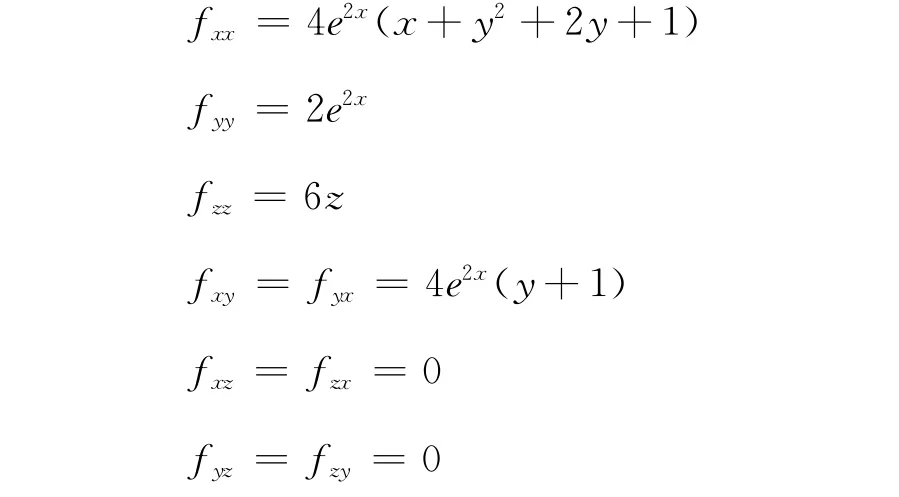
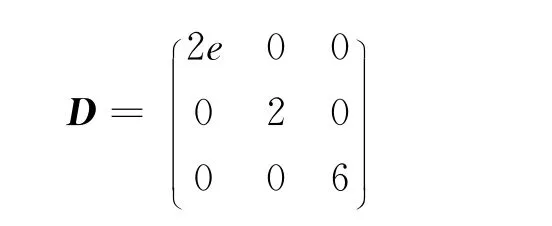
由定理2知，它是极小值点。

由定理2知，它不是极值点。

通过以上两方面应用，将实对称矩阵抽象的特性进行了运用，更加体现了它的实用价值。

［1］ 同济大学数学系.高等数学（下册）［M］.6版.北京：高等教育出版社，2007.

［2］ 华东师范大学数学系.数学分析（下册）［M］.4版.北京：高等教育出版社，2010.

［3］ 徐森林.数学分析（第三册）［M］.北京：清华大学出版社，2007.

［4］ 吴赣昌.线性代数（理工类）［M］.4版.北京：中国人民大学出版社，2011.

［5］ 黄益生.高等代数［M］.北京：清华大学出版社，2014.

［6］ 杨文茂.空间解析几何［M］.武汉：武汉大学出版社，2004.

［7］ 纪跃芝.用矩阵的正定性判定多元函数的极值［J］.吉林工学院学报，1995，16（4）：71－75.