随机利息力ARCH模型下的递增定期寿险

李 婷， 刘凌晨

（1.山西大学商务学院，山西 太原 030031；2.南开大学 经济学院，天津 300071）

0 引 言

人寿保险是一项长期性的业务，利率和死亡率是寿险精算业务中要考虑的最重要的因素。在传统的精算当中，利率假定是一个常数，但利率具有很强的随机性，会随着经济、政策等一系列因素发生变化。对于保险公司，如果假定利息力是一个常数，其随机性带来的风险将会消失，在这种假设情况下，存在的只有死亡风险。纵观目前金融市场，这一假定完全不符合现实情况，所以，研究利息力的随机性具有重要的理论意义和实际意义。

传统的精算模型当中，假定利率是一个常数，但实际上利率具有很强的随机性。1971年，Pollard J.H.［1］首次把随机利率引入精算领域，将利率作为随机变量引入精算函数进行研究。1976年，Boyle［2］假设利息力产生自白噪声，研究了随机利息力对精算函数的影响，结果表明，利息力在连续期间上存在相关性。1990年，Frees［3］研究了随机利息力MA（1）模型，推导出了利息力的期望和方差。1994年，Haberman［4］把文献［3］的可逆的一阶平均移动模型推广到随机利息力MA（2）模型，推导出了生存年金的一阶、二阶矩，但仍有其不足。1997年，Haberman［5］对随机利息力移动平均模型改进，研究了随机利息力AR（1）模型的矩母函数。1998年，Dhaene［6］在Haberman的一阶自回归模型基础上进一步研究了利息力AR（2）模型的矩母函数及其性质，但该模型的主要不足是利息力的方差为一常数。2001年，Perry等［7］进一步研究了AR（p）利息力模型下生存年金精算现值。国内学者师应来和蔡超［8］、解强和李秀芳［9］研究了随机利息力ARMA（p，q）模型下的企业年金精算现值和生存年金精算现值问题，其不足是假定利息力的残差序列相互独立且方差是定值。郭芳［10］建立随机利息力ARCH模型，弥补了ARMA（p，q）模型的不足。文中基于随机利息力ARCH模型，推导出递增n年死亡保险保费公式、准备金计提公式指出了随机利息力ARCH模型在保险精算业务中的应用性。

1 预备知识

设δt是区间（t－1，t］上的利息力，则自回归条件异方差ARCH模型为：

其中a0，a1，…，at和l1，l2，…，lq为已知。

引理1 未来k时刻单位价格1在0时刻的精算现值为：

引理2 在随机利息力ARCH模型下，未来k时刻1单位价值的精算现值为：

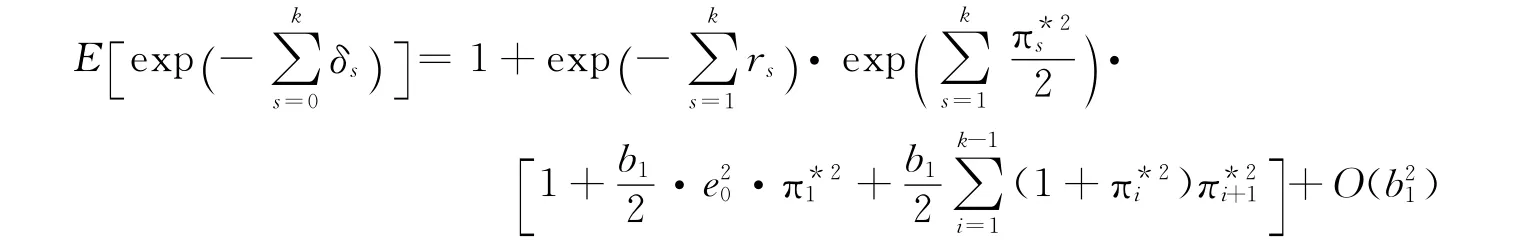
其中

2 基于随机利息力ARCH模型下的递增n年定期寿险

假设x岁的人（x）投保离散型的按算术数列递增的n年期定期寿险，即若保险人在第k＋1个保单年度内死亡，则在该年年度末支付保单受益人（k＋1）元（k＝0，1，2，…，n－1），假定均衡纯保费P，每期期初缴纳，δk是（k－1，k］年度的利息力，为方便计算，定义两个随机变量：

则递增定期寿险的损失变量为：

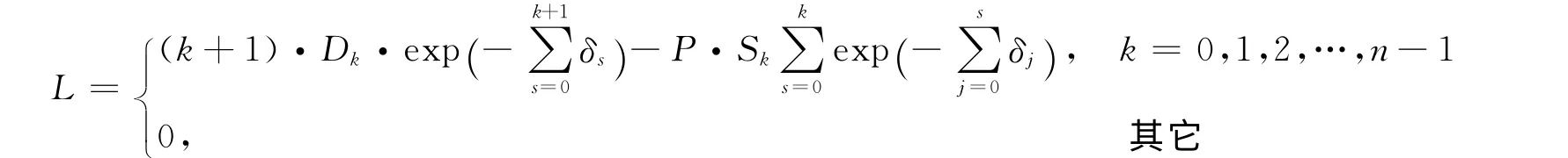
定理1 假设死亡率与利息力相互独立，则递增的n年期定期死亡保险投保人的均衡纯保费P为

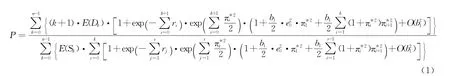
证明 由等价定理及随机利率与随机死亡率相互独立得：

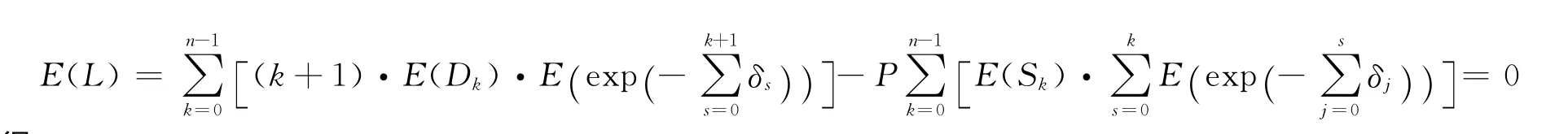
得

将引理2代入上式，并整理得

定理2 假设在递增的n年期定期寿险中，随机死亡率与随机利率相互独立，投保人的均衡纯保费为P，则保险公司对该保单在第k年的责任准备金：

证明 保险人在k时的未来随机损失变量为：

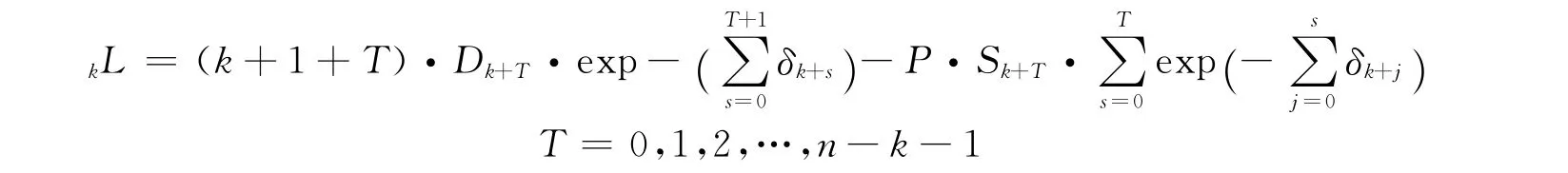
记kV＝E（kL），则由引理2可得：

将定理1得到的均衡保费P代入上式，并整理得

3 结 语

传统的精算模型当中，假定利率是一个常数，但利率具有随机性。自回归移动平均模型用残差来代替一系列因素对利率产生的波动影响，是较为符合实际情况的一种方法，比假定利率是常数更有说服力。而随机利息力ARCH模型主要考虑到异方差性，该因素比ARMA模型更加符合现实情况。文中正是基于随机利息力ARCH模型给出更为符合客观结果的递增n年死亡保险保费公式、准备金计提公式。保险公司根据更为符合客观结果的ARCH模型厘定保费和计提准备金，从而尽可能降低风险，稳定经营。

［1］ Pollard J H.On fluctuating interest rates［J］.Bull.Assoc.Roy.Actuaires Belge，1971，66：68－97.

［2］ Boyle P P.Rates return as random variables［J］.Journal of Risk and Insurance，1976，43（4）：693－713.

［3］ Frees E W.Stochastic life contingencies with solvency considerat ions［J］.Transaction of Societies of Actuaries，1990（42）：91－148.

［4］ Haberman S，Sung J H.Dynamic approaches to pension funding［J］.Insurance：Mathematics and Economics，1994，15（23）：151－162.

［5］ Haberman S.Stochastic investment returns and contribution rate risk in a defined benefit pension scheme［J］.Insurance：Mathematics and Economics，1997，19（2）：127－139.

［6］ Dhaene J.On approximating distribution by their de pril transforms［J］.Scandinavian Actuarial Journal，1998（1）：1－27.

［7］ Perry D，Stadje W.Long－Termstochastic interest rate models［J］.Insurance Mathematics Economics，2001（29）：73－82.

［8］ 师应来，蔡超.基于ARMA（p，q）模型的企业年金精算研究［J］.数量经济技术经济研究，2008（11）：127－136.

［9］ 解强，李秀芳.基于ARMA（p，q）利息力生存年金精算现值模型［J］.数学的实践与认识，2009（3）：74－79.

［10］ 郭芳.随机利率下的寿险精算模型研究［D］.北京：北京交通大学，2008.