基于支持向量机和HMM的音频信号分类算法

陈戈珩， 胡明辉， 吴天华

（长春工业大学 计算机科学与工程学院，吉林 长春 130012）

0 引 言

在多媒体技术的飞速发展形势下，基于内容的音频检索技术在多媒体、网络等领域正发挥着极其重要的作用和应用价值。由于音频信号除了含有一些基本的信息如编码方法、量化精度、采样率等注册信息外，由于语音信号本身就是一种缺乏内容语义的符号表示和缺乏结构化组织的二进制流，这直接使音频信号的检索问题受到非常大的限制。因此，对于如何提取相关音频信号中的内容语义和结构化信息，使无序的音频变得有序化，是实用化音频检索的关键技术。音频信号的自动分类是提取音频信号的结构和内容语义的重要手段，是音频分析和音频检索的研究热点。

在众多的分类方法中，基于隐马尔可夫（HMM）［1］的 分 类 方 法 和 基 于 支 持 向 量 机（SVM）［2］的分类方法是当前比较常用的两种方法。本质上隐马尔科夫模型是一种双重的随机过程，它对时间的随机统计特性具有极强的刻画能力，对连续的动态音频信号的多类分类具有较好的效果。支持向量机是基于统计学理论发展起来的机器学习法［3］，更大程度反映各类别间的不同，主要用于两类之间。

隐马尔科夫模型是经典的统计估计方法之一，它对动态时间序列具有很强的建模能力，且计算量较小。这种方法的局限性在于对先验知识的过多依赖，利用这种方法需要预先知道样本参数的分布形式，在现实中很难做到。支持向量机采用结构风险最小化准则代替了经验风险最小化准则，并结合神经网络［4］、机器学习、统计学习等方面的技术，在解决分线性、高维和小样本的问题中表现出诸多特有的优势。

1 音频特征分析

在对音频数据进行分类之前，首先对原始音频数据进行特征提取。因此音频数据分类的关键所在是进行特征分析，对音频特征的选取较为严格，既要能够充分表示音频的时域特征，又要很好地表示频域特征，为减少环境对特征的影响，要求其具有一般性和鲁棒性。对原始音频数据首先进行预处理以减少尖锐噪声（音频的采样率为22.050kHz），其次将对音频数据进行分割，分割成1 000ms的clip（22 050个采样），相邻的两个片段没有重叠的部分，对每一clip加25ms的Hamming窗形成帧，相邻帧间有12.5ms的数据重叠，最后计算每一帧的傅里叶变换系数F（w）和频域能量：

fs——采样频率。

根据音频帧计算以下基于clip的音频特征。

1.1 静音比例

在一个音频段中所含的静音帧与总的帧数的比：

一般来说，由于语音的连贯性不是很强，音乐相对较连贯，所以语音的静音比例要比音乐的静音比例高很多。

1.2 子带能量比均值

将频域划分为4个子带区间sbi（i＝0，1，2，3），分 别 为，并计算各子带的能量为：

在频域中各子带能量与总能量的比值称为子带能量比：

片段中的各帧子带能量比的均值被称为子带能量比均值。

1.3 带宽均值和频率中心均值

1.3.1 频率中心均值

片段中音频的帧频率中心的平均值。频率中心是度量音频亮度的指标：

1.3.2 带宽均值

片段中所有音频帧的带宽的平均值。带宽是衡量音频频域方位的指标：

语音的带宽范围一般在0.3～3.4kHz左右，音乐的带框比较宽，一般在22.050kHz左右。

1.4 高过零率比率［5］

由于语音是由清音和浊音的不断交替构成，因此语音的过零率的变换要高于音乐信号的过零率。如果设定一个过零率的阈值，那么在一个音频段中，可以计算出高于这个过零率的帧在整个段中所占的比例。这个比例就是高过零率比率，简称HZCRR。

ZCR阈值一般为一个片段中ZCR平均值的1.5倍，N为一个片段中总帧数，ZCR（n）是第n帧的过零率。

1.5 低频率能量比率

语音信号比音乐信号中含有更多的静音帧。如果设定一个能量的阈值，那么在一个音频段中可以计算出低于这个阈值的帧在整个段中所占的比例。这个比值就是低频率能量比，简称LFER。

式中：N——一个片段中的总帧数；

E（n）——第n帧的频域能量；

AVE——片段中各帧能量的均值。

1.6 基音频率标准方差

基因频率的标准方差是用来表示在一个片段中基因频率变化范围的大小。

1.7 频谱迁移

频谱迁移是指在音频片段中所有相邻帧频谱之间的平均差异。频谱变迁的公式为：

1.8 和谐度

一个片段中基音频率不等于0的帧数所占总帧数的比例称为和谐度，比例越大，和谐度越高。

1.9 平滑基音比

如果第i帧与第i－1帧的基因频率的差值小于一定的范围，并且第i帧的基因频率非0，则第i帧称为基因平滑帧。一个片段中平滑基因比是指平滑帧占基因频率大于零的帧数之比。

在以上分析中，由于段特征是在帧特征基础上计算得来的，所以先提取了音频数据的帧特征。音频数据分类的特征集合是在段特征基础上构造出来的，但是不同音频特征的值有很大程度的差异，因此要先进行归一化处理。公式如下：

式中：xi——提取出来的原始特征；

ui——均值；

σi——方差；

由于MFCC［6］归一化处理后的实验结果不理想，所以对MFCC不做归一化处理，对一个片段中的各帧计算12维MFCC系数以及MFCC的一阶差分序列，然后在片段内对各维取平均值，作为该片段的MFCC特征值。这样有11维段层次的基本特征加上24维MFCC特征值组成35维的特征向量集作为分类器的输入。

2 分类器设计

由于音频是一个随机过程，所以其特征具有一定的时间统计特性。因此，所提出的音频分类方法应该能够充分的表征音频数据的时间统计特性。为了克服隐马尔科夫模型在识别过程中的错误识别率和支持向量机对两类问题分类的不足，文中对一些文献采用的HMM和SVM相结合的方法进行改进。基于HMM与SVM相结合的算法流程如图1所示。

图1 基于HMM与SVM相结合的算法流程

将音频片段分为4类：带背景音的语音、纯语音、音乐和静音，首先选取能量和过零率特征，利用基于规则的分类方法识别出静音片段，识别规则如下：

式中：avZCR——该片段所有音频帧ZCR的均值；

avE——该片段中所有的音频帧频域能量均值。

如果同时满足以上两个规则，那么该片段是静音片段。

2.1 HMM分类器设计

HMM本质上是在隐马尔科夫链的基础上发展而来的一种双重随机过程。一种是描述数据状态转移的马尔科夫链，它是基本的随机过程。另一种是描述观察值间和状态的对应关系。HMM模型采用Baum－Welch重估算法进行训练，这种算法很好地解决了HMM在参数估计方面的难题，并为各类模型计算参数，从而得到对应的HMM（记为λi，i＝1，2，3）模型。基本思路是按照某种重估算法根据现有的模型λ′估计出模型λ，最终使得P（O／λ′）＜P（O／λ）。用λ替代λ′重复上述过程直到模型参数处于收敛状态，得到最大似然模型。

对需要进行分类的音频数据，首先需要通过HMM分类器进行识别判定，然后计算出每个音频在HMM模板下的最大输出概率和次最大输出概率，并使其差值与阈值（此阈值是根据MCE准则设定的）进行比较。如果阈值大于差值，则再采用SVM分类器进行识别得出最终判定结果，否则结果直接由HMM分类器判定给出。

HMM分类器结构如图2所示。

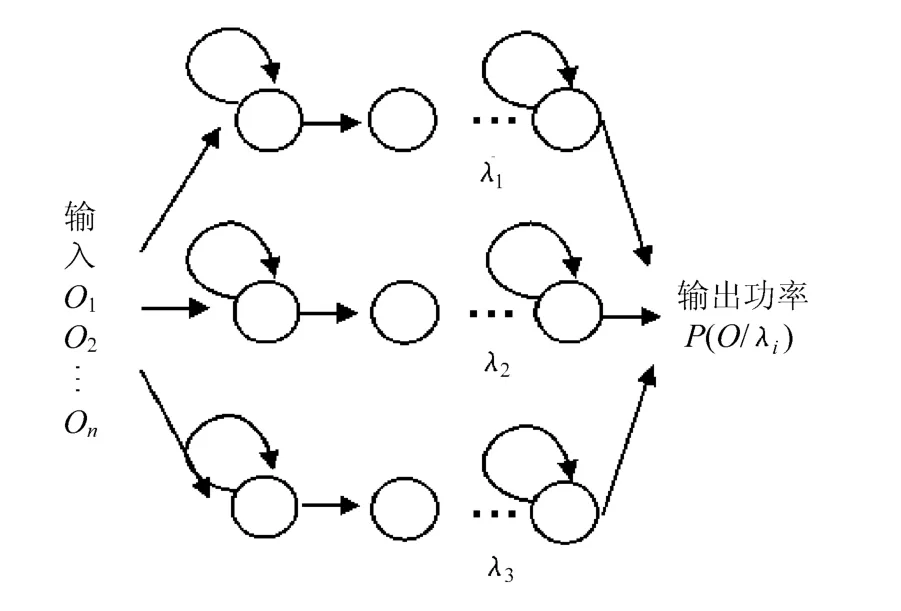
图2 HMM分类器流程图

2.2 SVM分类器设计

与其他方法相比，支持向量机［7］是在坚实的数学理论基础上发展起来的一种新型的分类方法，它采用结构风险最小化准则代替经验风险最小化准则，同时结合了神经网络、统计学习和机器学习等多方面的技术。这种方法通过引入核函数将样本向量映射到一个更高维的空间里，即将当前输入空间的非线性问题转化为高维特征空间的线性问题，在这个空间里建立一个最大间隔超平面，将空间中两类样本正确分开，并取得最大边缘。由于不同的核函数构造的输入空间不同，线性决策面的学习机也不同，从而得到的支持向量也不同。

图3 SVM分类器流程图

常用的核函数有［8］：

线性内核函数：

径向基核函数：

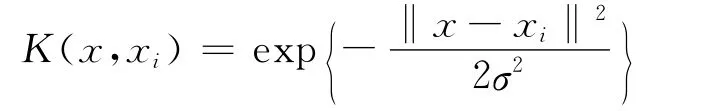
多项式核函数：

K（x，xi）＝［（x·xi）＋1］d

S

igmoid核函数：

K（x，xi）＝tanh［b1（x·xi）＋b2］

在构造分类器之前首先要提取基于帧的特征和段的特征，根据分类需要选择不同的特征向量集。为了降低不同类别的特征向量在分类过程中带来的负面影响，对特征数据进行归一化处理。为了降低计算成本，提高分类效率，根据不同支持向量机的核函数在分类过程中表现出的优缺点来进行径向基核函数［9］的选择。根据不同参数和特征向量的选择，经过反复的训练测试得到最满足分类目的的分类器。选择径向基核函数为分类函数，即

经最优化求解得决策函数为：

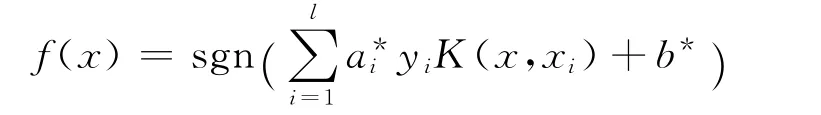
对HMM模型分类的结果进行分析，如果音频数据需要SVM分类器对其进行二次分类，则根据需要对分类器进行选择。在进行二次分类前首先构造SVM区分纯语音和音乐，构造SVM区分出语音和带背景的语音。这种方法满足了支持向量机对小样本的分类条件，同时提高了分类的效率和精度。文中训练3个径向基核函数支持向量机作为分类器，径向基函数参数σ选取为10。

3 实验结果

音频数据来源于CCTV－1、CCTV－2等电视台，广播和CD音乐，内容包括新闻、天气预报、综艺节目、人物访谈、流行音乐等。采样率是22.050kHz，精度16位，存储格式为wav格式，时间长度为200min，语音为57.6min，音乐63.2min，带背景语音为56.4min，静音片段为22.8min。各类音频的2／3为训练样本，1／3为测试样。

在实验前所有音频数据都被分割为10s长的片段，文中利用基于规则的分类方法对静音做阈值分析，将静音从语音库中识别出来，故可以不必训练分类器。在训练阶段将2／3的样本手动的分为语音、音乐、带背景语音，然后训练HMM和SVM分类器。测试阶段用另外1／3的数据进行测试，记录并计算分类精度。

实验结果见表1。

表1 基于HMM和SVM两级分类器的分类结果

从结果可以看出，分类的正确率分别为静音95.55%、语音96.46%、带背景音89.18%、音乐96.80%，明显优于文献［10］采用HMM分类器分类的分类结果：语音88.01%；音乐95.96%；语音＋音乐81.03%。为了降低分类的复杂度，提高分类效率，文中对不同类别进行了有针对性的分类。

4 结 语

针对音频数据的自身特点将隐马尔科夫和支持向量机两种方法相结合，HMM不但对音频信号具有很好的描绘能力，还对大量数据具有很好的分类效果，弥补了SVM在大量数据分类中的不足，SVM则克服了HMM分类上的不足，使在数据量上的要求大大的降低。文中首先进行阈值的判别，满足条件则利用SVM分类器进行二次分类，这样不但减少了时间，还大大地调高了识别率。

［1］ 杨会云.基于HMM－SVM的音频分类与检索算法研究［D］.重庆：重庆邮电大学，2010.

［2］ 辛庆正.基于支持向量机的语音识别技术［D］.天津：河北工业大学，2009.

［3］ Vapnik V.The nature of statistical learning theory［M］.New York：Springer－Verlag，1995.

［4］ 唐军.基于HMM与小波神经网络的语音识别系统研究［D］.南京：南京理工大学，2007.

［5］ 王超.基于小波和隐马尔可夫模型的音频分类［D］.西安：西北工业大学，2007.

［6］ 王超，吴亚锋.基于EMGD－HMM的音频自动分类［J］.电声技术，2007（7）：53－60.

［7］ 史东承，韩玲艳，于明会.基于HMM／SVM的音频自动分类［J］.长春工业大学学报：自然科学版，2008，29（2）：178－182.

［8］ 李仕强.基于内容的音频分类与识别［D］.南京：南京信息工程大学，2010.

［9］ 曹兆龙.基于支持向量机的多分类算法研究［D］.上海：华东师范大学，2007.

［10］ 卢坚，陈毅权，孙正兴，等.基于隐马尔可夫模型的音频自动分类［J］.软件学 报，2002，13（8）：1593－1597.