基于希尔伯特-黄变换的信号处理方法
宋 宇, 游海龙, 翁新武, 李 嵩, 宋隽炜
(长春工业大学 计算机科学与工程学院,吉林 长春 130012)
0 引 言
传统的信号处理方法是将数据进行傅里叶变换,再对傅里叶谱进行数据分析,但这种方法有很大的局限性,也就是数据严格周期平稳或宽平稳。虽然针对传统傅里叶变换许多学者提出了一些改进措施,例如功率谱、小波分析等,但这些归根结底还是基于傅里叶分析,还是局限在线性系统。
1998年,N.E.Huang等人研究出了一种新方法,这种方法主要包括两部分:一是先对信号进行经验模式分解(EMD),EMD方法由黄锷博士提出;二是在EMD方法的基础上利用了Hilbert变换[1],这种方法分析高频数据,减小高频噪声[2],同时这种方法会产生一个内在模式函数(IMF)集。IMF表达式有益于进行希尔伯特变换,从而计算出瞬时频率。
1 希尔伯特-黄变换相关基本理论介绍
1.1 瞬时频率
对于任何信号的频谱分析都会用到频率这个概念。但对于非线性非平稳信号的处理,频率时刻在变化,对于这种信号的处理需要引入一个新的概念,那就是瞬时频率。在傅里叶变换分析处理信号时,瞬时频率是要定义在整个信号数据长度上,并且要有连续振幅的余弦或者正弦函数。瞬时频率是整个数据的一个扩展,非平稳数据的频率随时在改变,所以一个相对于完整信号的局部信号没有意义。任意一个时间序列X(t),都有它的希尔伯特[3]变换Y(t):
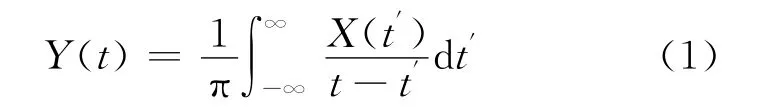
这个定义下的X(t)和Y(t)为复共轭对,所以可以获得解析信号Z(t):

这里

经过Hilbert变换,瞬时频率则定义为[4]:

1.2 本征模函数(IMF)和经验模式分解(EMD)
在实际应用中,非平稳信号处理对其瞬时频率的分析需要构建一种基于自身时间序列的函数,这样对瞬时频率的分析才有意义。这种函数必须是局部均值为零而且对称,并且具有相等的过零点数和极值点数目。为此,本征模函数的概念由N.E.Huang[5]等提出来,本征模函数对于任意一点的瞬时频率都有意义,这样本征模函数就可以应用于解决实际问题。满足经验模式函数的必要条件如图1所示。
在实际应用中,必须要将瞬时频率变得有意义,首先要做的是把一个数据集合削减成IMF的分量。这样对于复杂数据在一个局部时间可以得到多个瞬时频率。这种得到IMF的方法就是经验模式分解法(EMD)。

图1 满足经验模式函数的必要条件
1.3 希尔伯特谱
根据前文所述,可以对非平稳信号进行EMD,得到我们所需的各个IMF,即,C1,C2,…,Cn。
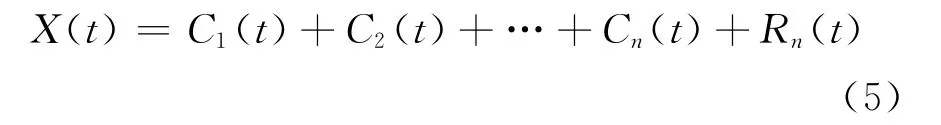
根据式(1)~式(4),得出所有IMF的瞬时频率和幅度都是时间t的函数。
3个变量a,ω,t互相相关,如三维平面的3条坐标轴。可以很容易得到分别以(ω,a),(ω,t),(t,a)为底的三维图像。每一个三维图像都可以体现希尔伯特谱。而(ω,t)函数的幅度a,叫做希尔伯特幅度谱[6]H(ω,t)。
1.4 边际谱
综上,可以定义希尔伯特边际谱h(ω)为[7]
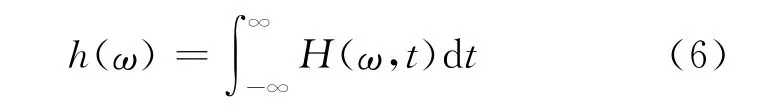
上式中的h(ω)表示在单位频率内的幅度分布情况,它表现了一个信号段内每个幅度分布概率之和。
2 利用希尔伯特-黄变换实现方法
经验模式函数的引入使得HHT相比传统的信号处理方法具有了创新的地方。因为经验模式函数具有信号的局部时间特性,这使得在实际信号处理中能够获得有实际意义的瞬时频率。经验模式分解最后要使每一个IMF有意义。设一个时间序列X(t),它的上、下包络分别是u(t)和v(t)。这样上下包络平均曲线m(t)可以表示如下:

通过移动后,得到余项h1(t):
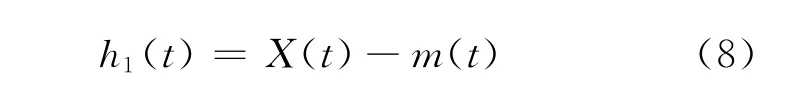
通过对比定义IMF的必要条件,h1(t)都满足,则h1(t)应该就是IMF。实际上,通过分解得到的h1(t)并不严格满足IMF的必要条件[8]。因此要再用h1(t)来代替原始信号。假设与h1(t)相应的上、下包络线分别是u1(t)和v1(t),再重复以上过程,则:

直到所得的hk(t)都满足IMF条件。这样就分解获得了第一个经验模式函数。C1(t)和信号的剩余项设为r1(t),即:
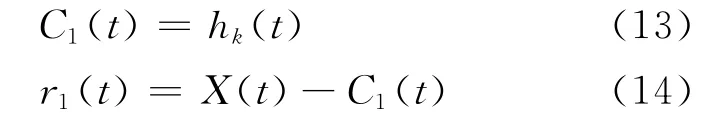
最后再对r1(t)进行经验模式分解,分解到剩余项部分是一个单调增或减的信号,或者它的值小于之前给定的数据时,这样就停止继续分解。最后经过分解获得了所有的IMF和余量,即:
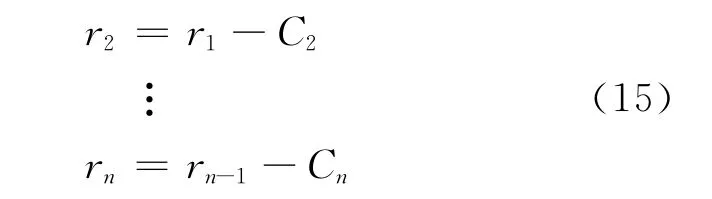
就得出原始信号X(t),可表示为:

3 利用基于EMD分解方法应用于铝电解阳极效应检测
对阳极震动信号的分析主要包括:信号分析、信号测量及提取、状态诊断和状态分析4个内容。
用EMD方法对发生阳极效应的振动信号做EMD分解,提取IMF,得到分解图如图2所示。
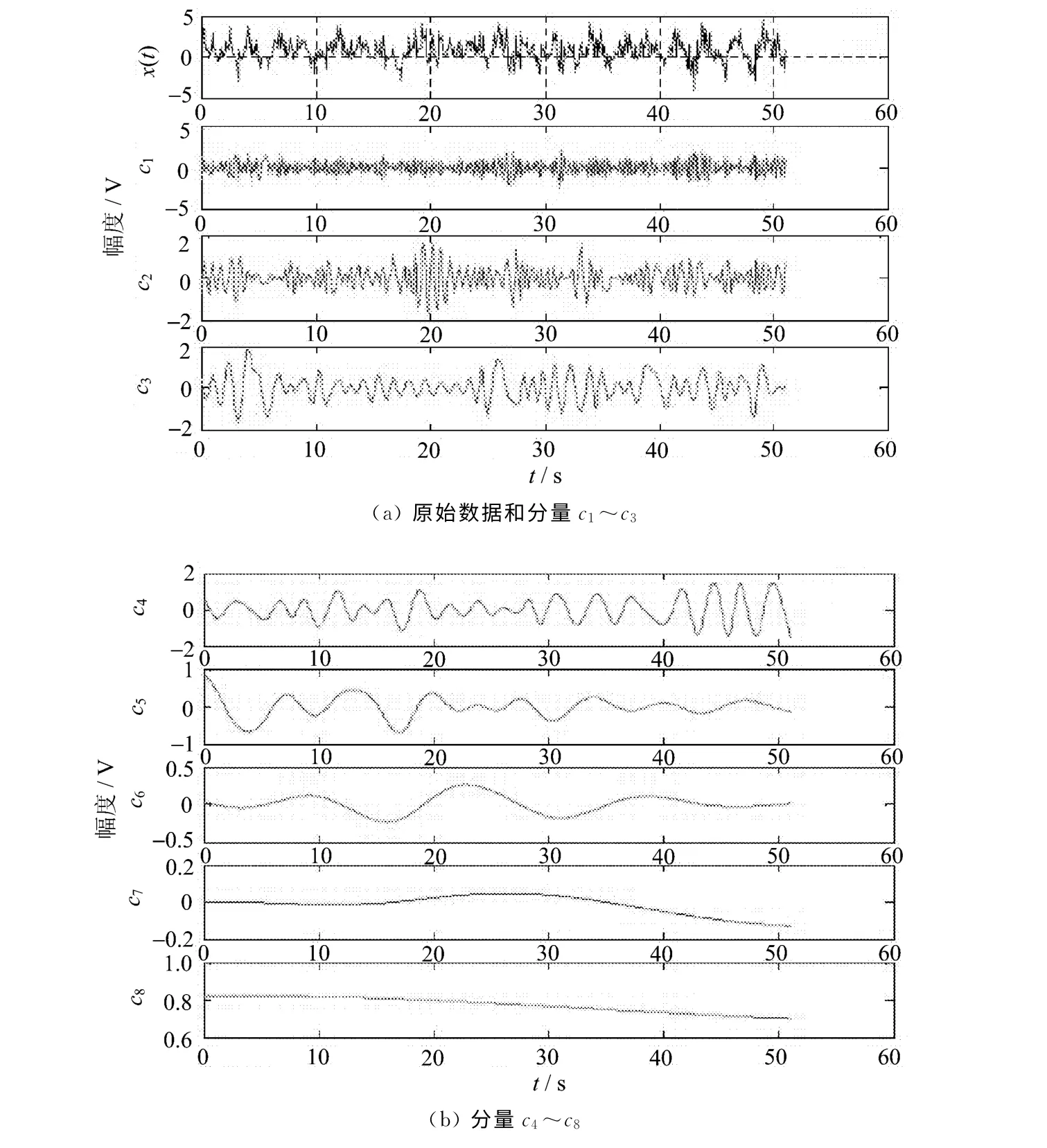
图2 对阳极效应振动信号的EMD分解
图中:注意最后一个分量c8,不是IMF,是个变化趋势,而对无阳极效应的阳极振动信号做EMD分解,如图3所示。

图3 对无阳极效应振动信号的经验模式分解
原始数据和取前5阶IMF分量c1~c5。
经过EMD分解后,我们对振动信号IMF的谱进行研究。文中要研究振动信号IMF的伯格谱,先求出原始信号的伯格谱如图4所示。
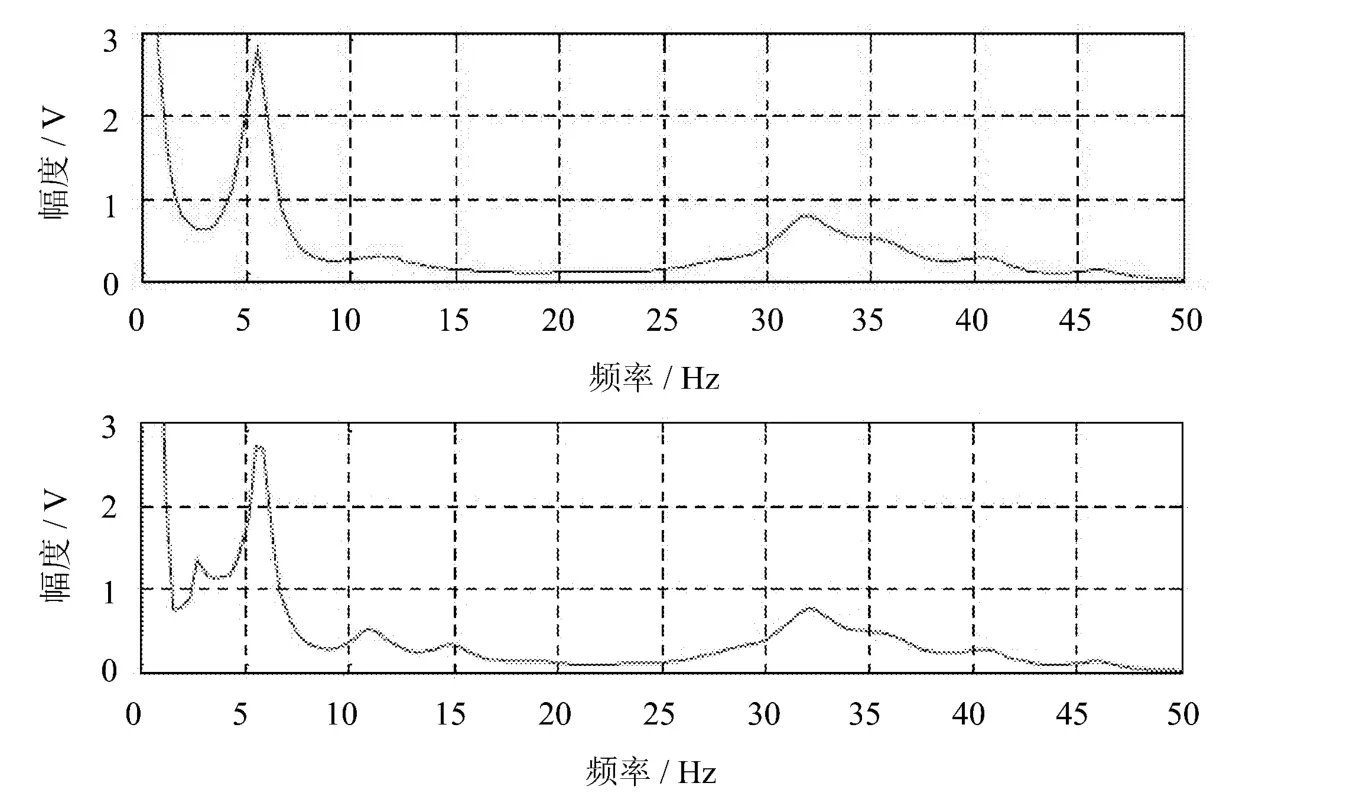
图4 没有经过EMD分解得到的伯格谱
在图3中,我们对振动信号进行了EMD分解得到了振动信号的各阶IMF,求得各阶IMF的伯格谱之和,如图5所示。
通过观察图5,它是对原始信号的各个IMF的伯格谱之和。伯格谱出现尖峰的位置是在频率8Hz和12Hz[9]。实验结果与实际结果一致,这表明利用基于EMD获得信号IMF可以得到比较高的信噪比。在铝电解阳极效应检测中这种方法可行、高效。
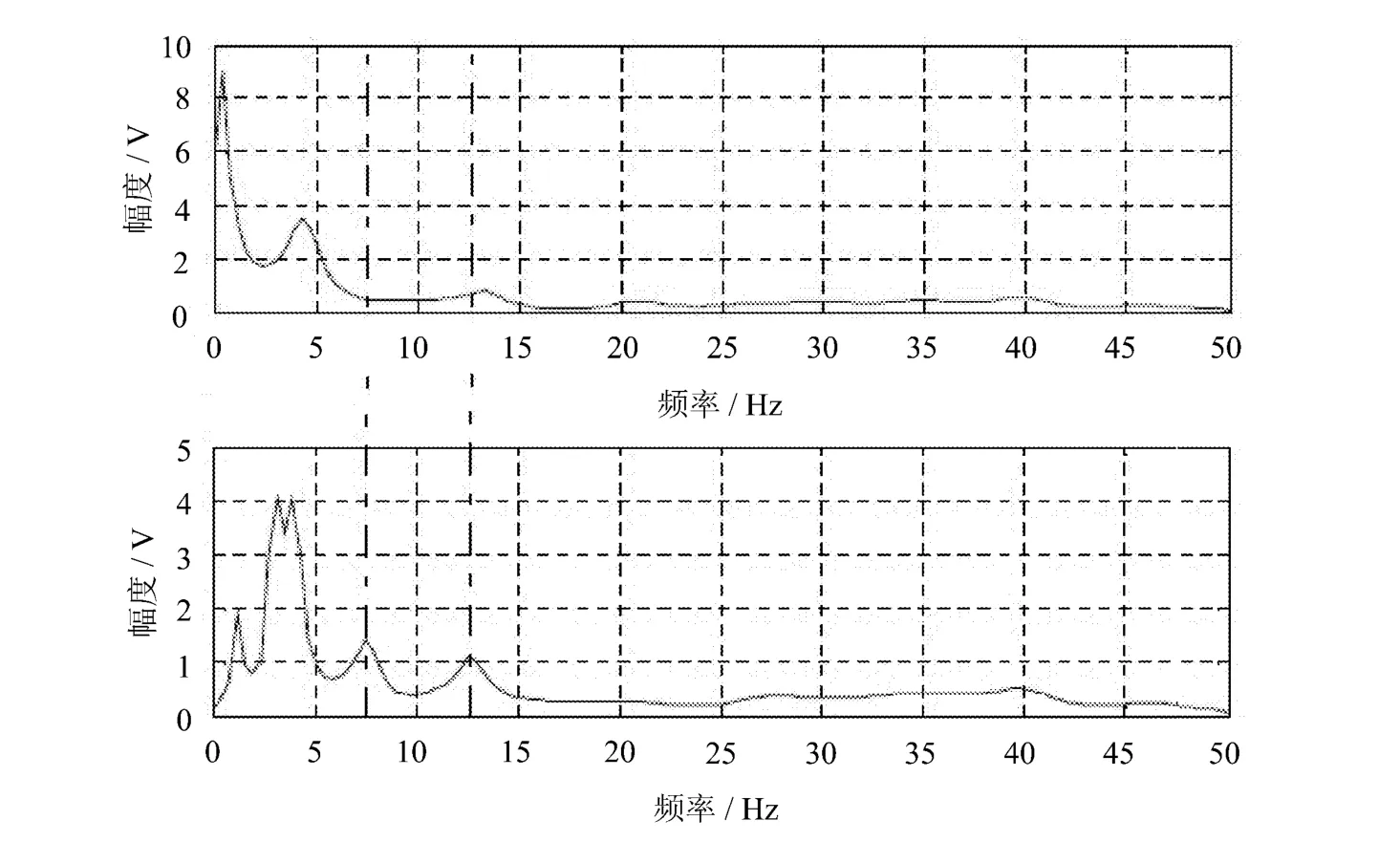
图5 经过EMD分解获得的信号伯格谱
4 结 语
利用HHT对阳极效应信号特征的提取和识别很有效,误差小,这种方法相对于傅里叶变换更具有对非线性和非平稳信号的处理能力,在未来的应用中将会越来越广泛,但一种新方法的提出还有很多不足的地方,在以后的应用中不断探索和改进。
[1] 宋国锋,董小刚,秦喜文.EMD方法在高频数据中的应用[J].长春工业大学学报:自然科学版,2013,34(6):601-605.
[2] 张狆.基于EMD去噪方法研究[J].电脑知识与技术,2010(35):195-197.
[3] 徐汉生,何平,赵联文.应用统计[M].西安:西安交通大学出版社,1994.
[4] N E Huang,Z Shen,S R Long,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[D].Proc.R.Soc.Lond,1998,454(A):903-995.
[5] N E Huang.Review of empircal mode decomposition analysis[J].Proc.of SPIE,2001,4391:71-79.
[6] W Huang,Z Shen,N E Hang,et al.Engineering analysis of biological variables an example of blood pressure over 1day[J].Proc Natl.Acad.Sci.,1998,95:4816-4821.
[7] 钟佑明,秦树人,汤宝平.希尔伯特-黄变换中的边际谱的研究[J].系统工程与电子技术,2004,26(9):45-49.
[8] 胥保春,袁慎芳.IMF筛选停止条件的分析[J].振动、测试与诊断,2011(3):69-71.
[9] 王志宏.浅谈铝电解的阳极效应[J].山西冶金,2001(2):108-110.

