横观各向同性地基上薄圆板弯曲解析解

刘晓梅 姜 旭

(1.华侨大学厦门工学院，福建 厦门 361000； 2.福建省双阳建筑工程有限公司，福建 厦门 361000)

横观各向同性地基上薄圆板弯曲解析解

刘晓梅1姜 旭2

(1.华侨大学厦门工学院，福建 厦门 361000； 2.福建省双阳建筑工程有限公司，福建 厦门 361000)

结合板的边界条件、控制方程及板—地基的相容条件解出控制方程中的待定系数，将横观各向同性弹性半空间地基上薄圆板受竖向荷载作用的弯曲问题转化为数值积分和代数方程组的求解，算例结果表明：在求板的位移时该级数解答仅取前几项就可达到很好的精度，收敛速度快。

横观各项同性，薄圆板，弯曲，傅立叶—贝塞尔级数，Hankel变换

0 引言

弹性地基板在实际工程中有着广泛的应用，前人已对温克尔地基及双参数地基上板的弯曲进行过充分的研究，对各向同性弹性半空间地基上板的弯曲也有所研究[1,2]。天然地基土在横向和竖向具有不同的力学特性，考虑到土体的应力—应变关系，将地基土作为横观各向同性弹性半空间模式处理较切合实际。本文利用傅立叶—贝塞尔级数，结合板的边界条件、控制方程和相容条件，将横观各向同性弹性半空间地基上薄圆板受竖向荷载作用的弯曲问题转化为数值积分和代数方程组的求解。

1 横观各向同性弹性半空间的解答

设：

(1)

并引入以下应力组合：

T1n=τθzn+τrzn,T2n=τθzn-τrzn

(2)

(3)

式(3)中：

其中，A，B，C，D，E和F为待定系数。

(4)

注意到式(2)，进行Hankel变换后，则式(4)可表示为：

(5)

把式(3)代入到式(5)中，解出A～F的表达式,其中C=D=F=0，可求得弹性半空间表面在竖向荷载下的沉降，并将其进行Hankel变换后得到：

(6)

其中：

L1=(c13+c44)c11(s1-s2)；

(7)

2 弹性半空间地基上薄圆板弯曲的傅立叶—贝塞尔级数解

设周边自由的薄圆板，半径为a，置于横观各向同性弹性半空间地基上，则其控制方程为：

D22w(r,θ)=q(r,θ)-p(r,θ)

(8)

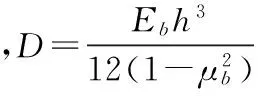
将圆板的边界条件用挠度表示为：

(9)

(10)

设w，q和p可展开为下列形式的傅立叶—贝塞尔级数[4]，即：

(11)

(12)

(13)

其中：

(14)

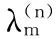
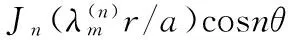
(15)

将式(11)代入边界条件式(9)和式(10)中，比较所得式中cosnθ的系数，得：

(16)

(17)

将式(13)中的pn(r)也按傅立叶—贝塞尔级数进行展开，并进行n阶Hankel变换得：

(18)

假定板与地基接触面沿板中面方向光滑，并考虑到地基表面所受的竖向荷载与地基反力的关系，则由式(6)和式(18)得：

(19)

对式(19)进行n阶Hankel逆变换，得：

(20)

(21)

式(21)中：

(22)

式(22)中：

(23)

(24)

由板与地基的相容条件可以看出，在板与地基不发生脱离的情况下，z=0处板的挠度等于地基的挠度：

(25)

(26)

联立求解式(15)，式(16)，式(17)及式(26)这四个控制方程，可得到各待定系数wnm,pnm,An,Bn。

3 数值算例

板的参数如下：

a=6m，h=1m，μb=0.167，Eb=20GPa。

横观各向同性弹性半空间地基的计算参数如下：

E1=5MPa,E2=10MPa,μ1=0.25,μ2=0.25,G2=1.5MPa。

设板受到均匀分布的荷载q0=1N/m2，数值积分采用10节点高斯积分[5,6]。计算结果见图1。

计算结果表明：

1)在横观各向同性弹性半空间地基上的薄圆板的挠度随着r/a的增大而逐渐减小，挠曲线光滑、连续。

2)傅立叶—贝塞尔级数解法的计算精度与所取的级数的项数有关。

3)用傅立叶—贝塞尔级数解法求得的横观各向同性弹性半空间地基上薄圆板弯曲问题符合实际情况。

4 结语

本文借助于傅立叶—贝塞尔级数、Hankel变换与其逆变换，分析了横观各向同性弹性半空间地基上薄圆板受竖向荷载作用下的弯曲问题，采用比较系数法将复杂的偏微分方程转化为数值积分和代数方程组的求解，较其他方法更为简单，更具有一般意义，从而为基础工程的设计、计算提供了坚实的理论基础。

[1] 黄 义，何芳社.弹性地基上的梁、板、壳[M].北京：科学出版社，2005.

[2] Selvadurai A.P.S. Elastic analysis of a soil-structure interaction[M].New Jersey:Preenice-Hall,1978.

[3] 李 婕,张学民,顿志林，等.横观各向同性地基空间问题的位移函数解法[J].岩土工程学报,2007(1)：47-51.

[4] 严宗达.结构力学中的富里叶级数解法[M].天津：天津大学出版社，1989:198-203.

[5] 数学手册编写组.数学手册[M].北京：人民教育出版社，1979:550-553.

[6] 关 治，陆金莆.数值分析基础[M].北京：高等教育出版社，1998:210-219.

Analysis on thin circular plate bending solution on transverse isotropic foundation

Liu Xiaomei1Jiang Xu2

(1.XiamenCollegeofIndustry,HuaqiaoUniversity,Xiamen361000,China;2.FujianShuangyangBuildingEngineeringCo.,Ltd,Xiamen361000,China)

The paper finds out undetermined coefficients of governing equation by combining with boundary condition, governing equation, and compatibility conditions of board and foundation, and transforms thin circular plate bending under vertical load into numerical integration method and algebraic equations. Results show that: the plate displacement solution can achieve perfect accuracy by extracting several items, furthermore, its convergence rate is rather rapid.

transverse isotropy, thin circular plate, bending, Fourier-Bessel series, Hankel transformation

2014-12-17

刘晓梅(1984- )，女，硕士，讲师； 姜 旭(1982- )，男，工程师

1009-6825(2015)06-0081-03

TU433

A