求解贝塞尔类方程的推广试探函数法
那仁满都拉
(内蒙古民族大学 物理与电子信息学院,内蒙古 通辽 028043)
教学讨论
求解贝塞尔类方程的推广试探函数法
那仁满都拉
(内蒙古民族大学 物理与电子信息学院,内蒙古 通辽028043)
对本刊2014年第4期刊出的《求解贝塞尔类方程的试探函数法》一文给出的求解贝塞尔类方程的试探函数法做了进一步推广,给出了推广试探函数法.该方法能够求解更一般性的贝塞尔类方程.
贝塞尔类方程;推广试探函数法
在文献[1]中,我们给出了求贝塞尔类方程线性独立解的一种简单、直接的试探函数方法.该方法借助数学软件MAPLE或MATHEMATICA等,能够求解多种类型的较复杂的贝塞尔类方程,如在文献[1]中给出的虚宗量贝塞尔方程、球贝塞尔方程等等.但我们在后续的研究中发现,文献[1]中给出的试探函数法无法求解如下一类更一般性的贝塞尔类方程:
(1)
(2)
(3)
(4)
此类方程很多,这里只列出了4种,想更多了解可参阅文献[2,3].方程式(1)—式(4)的共同特点是它们的系数都是任意未知函数和未知函数的导数构成.因此,对这些方程的求解应该是更加困难.
本文针对这类更一般的贝塞尔类方程,推广试探函数法的应用,将给出一种推广的试探函数法.
1 推广试探函数法
在文献[1]给出的试探函数法中把贝塞尔类方程的试探解设为
y=f(x)Zν(λxk)
(5)
这里Zν(λxk)是柱函数,f(x)是任意待定函数,ν、λ(≠0)及k(≠0)是待定常数.这种试探解对于像方程式(1)—式(4)这类的系数为任意未知函数的贝塞尔类方程很难使用,主要原因是试探解(5)中柱函数的宗量是自变量x的幂函数形式.针对这一不足,本文推广了试探解的形式,使其假设为
y=p(x)Zν(q(x))
(6)
式中p(x)和q(x)是任意两个待定函数.把试探解(6)代入要求解的方程,利用数学软件MAPLE或MATHEMATICA进行计算和简化,并通过具体分析可确定待定函数p(x)、q(x)和待定常数ν,进而得到所求解方程的线性独立解.由于所求解方程式(1)—式(4)的复杂性,上述计算过程显得非常复杂,但借助MAPLE或MATHEMATICA等性能优良的计算软件,可以容易完成这些计算任务.下面通过举例来展示推广试探函数方法.
2 应用例子
例1.求贝塞尔类方程式(1)的线性独立解.
把方程式(1)的线性独立解设为
y=p(x)Jν(q(x))
(7)
把式(7)代入方程式(1)进行简化计算,并令贝塞尔函数Jν(q(x))和Jν+1(q(x))的系数分别为零,可得
(8)
(9)
求解方程式(9)可得
(10)
上式中q(x)是任意函数,为了具体确定此任意函数并使式(10)变得简单,可选取q(x)=f(x),则式(10)简化为
p(x)=f(x)μ
(11)
把式(11)代入式(8),进行简化计算可得
(12)
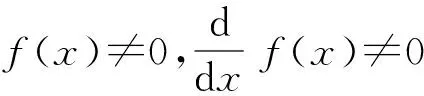
y=f(x)μJm(f(x))
(13)
例2.求贝塞尔类方程式(2)的线性独立解.
把方程式(2)的线性独立解设为
y=p(x)Jν(q(x))
(14)
把式(14)代入方程式(2)进行简化计算,并令贝塞尔函数Jν(q(x))和Jν+1(q(x))的系数分别为零,可得

(15)
(16)
求解方程(16)可得
(17)
把任意函数q(x)选为q(x)=f(x),则有
(18)
把式(18)代入式(15),进行简化计算可得
(19)
由式(19)可得ν=±m.因此,贝塞尔类方程式(2)的线性独立解为
(20)
例3.求贝塞尔类方程式(3)的线性独立解.
把方程式(3)的线性独立解设为
y=p(x)Jν(q(x))
(21)
把式(21)代入方程式(3)进行简化计算,并令贝塞尔函数Jν(q(x))和Jν+1(q(x))的系数分别为零,可得到两个方程.求解第二个方程(Jν+1(q(x))的系数)可得
(22)
把任意函数选为q(x)=g(x),则有
p(x)=f(x)g(x)μ
(23)
把式(23)代入第一个方程,进行简化计算可得ν=±m.故贝塞尔类方程式(3)的线性独立解为
y=f(x)g(x)μJm(g(x))
(24)
例4.求贝塞尔类方程式(4)的线性独立解.
把方程式(4)的线性独立解设为
y=p(x)Jν(q(x))
(25)
把式(25)代入方程式(4)进行简化计算,并令贝塞尔函数Jν(q(x))和Jν+1(q(x))的系数分别为零,可得到两个方程.求解第二个方程可得
(26)
把任意函数选为q(x)=g(x),则有
(27)
把式(27)代入第一个方程,进行简化计算可得ν=±m.故贝塞尔类方程式(4)的线性独立解为
(28)
总之,本文对前文给出的求解贝赛尔类方程的试探函数法做了进一步推广,给出了推广试探函数法.推广的试探函数法能够求解系数为任意未知函数和未知函数导数的更一般性的贝赛尔类方程.本方法的推出,对贝赛尔类复杂方程的求解与研究将起积极的促进作用.
[1]那仁满都拉.求解贝塞尔类方程的试探函数法[J].大学物理,2012,31(4):23-24.
[2]吴崇试.数学物理方法[M].北京:北京大学出版社,1999:449-452.
[3]E.卡姆克.常微分方程手册[M].北京:科学出版社,1977:515-517.
The extended trial function method for solving Bessel-like equations
Naranmandula
(College of Physics and Electronics,Inner Mongolia University for Nationalities,Tongliao,Inner Mongolia 028043,China)
Further extension of the trial function method proposed by earlier paper for solving linear independence solution of Bessel-like equations is presented and an extended trial function method is given. The extended trial function method can be used to solve more general type of Bessel-like equations.
Bessel-like equation; extended trial function method
那仁满都拉(1963—),男,内蒙古通辽人,内蒙古民族大学物理与电子信息学院教授,博士,从事非线性物理与计算物理的教学与研究工作.
教学讨论
O 441.1
A
1000- 0712(2016)06- 0008- 03

