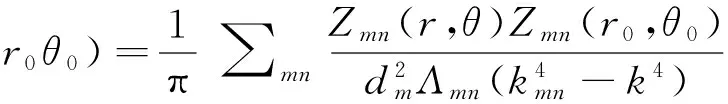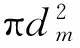内边界固定情况下环形薄板二维驻波的研究
方奕忠,沈 韩,王 钢,崔新图,廖德驹,冯饶慧
(中山大学 物理学院,广东 广州 510275)
物理实验
内边界固定情况下环形薄板二维驻波的研究
方奕忠,沈韩,王钢,崔新图,廖德驹,冯饶慧
(中山大学 物理学院,广东 广州510275)
通过极坐标下对竖向(垂直板面方向)的小振动方程分离变量,解出环形薄板的小振动方程在内边界固定外边界自由条件下解析解的简正模式,并在理论上和实验上对其二维驻波波节图形(克拉尼图形)进行了研究.实验上观察到仅有辐射状波节线(不包含内边界)或辐射状波节线与圆形波节线同时存在两种简正模式,进一步计算了此时薄板上的圆形驻波波节线的半径和方程的本征值所满足的规律以及薄板的弹性模量,并与实际测量值进行比较,发现理论结果跟实验符合得很好.
驻波;m阶贝塞尔函数;克拉尼图形; 环形薄板
自从1787年克拉尼首先发现水平放置的撒有稀薄沙粒的薄金属板上竖向小振动的二维驻波波节图[1](现称为克拉尼图形)后,对克拉尼图形的研究已有重要的进展和应用[2-6].当初克拉尼采用粗沙粒,发现沙粒聚集在波节线上形成规则且对称的图形,称为正(或标准)克拉尼图形.若所用的沙粒很细很轻,此时细沙会聚集在波腹上而不是在波节上,称为逆向克拉尼图形或克拉尼堆[7],又称法拉第堆[8].根据瑞利的记载[9],泊松计算了圆形薄板的低频端克拉尼图形的前几个圆形波节线的解析解及半径的理论值,萨伐尔在实验上进行了一系列的测量,证实了理论跟实验吻合得很好.上世纪90年代后期,宋力等人从纯理论上研究了弹性地基上圆环形薄板的振动问题[10-12],但他们只是求出了低频时振动方程的前几个特征根,而没有求出严格解的简正模式及共振时各种频率下的波节线的半径,没有给出薄板的弹性模量和二维驻波图,也没有实验的验证.到目前为止,对克拉尼图形的研究除了本文作者之前的工作[13,14]以外,其他研究工作还有圆形薄板[9]、方形薄板[9,15]、体育场形状薄板[6,16]和小提琴形薄板[16]等模型,且仅限于中低频段[9,16],即f<6kHz.对薄板的弹性振动还有其他报道[17,18],但对内边界固支下环形薄板的高低频段的克拉尼图形的研究理论上或实验上均尚未见报道.在通常的弹性力学或理论声学教科书和参考书中[19,20],对薄板的小振动通常仅求解部分边界固支、简单支承或弹性支承的情形,对全部边界悬空(即自由边条件)的情形只指出求解方法而很少求解,这是因为该条件下求解比较困难,需要进行数值计算.
类似圆形薄板的情形[9,14],本文对环形薄板的小振动偏微分方程采用极坐标系进行分离变量,把四阶偏微分方程降为二阶,求解内边界固定外边界自由时环形薄铜板的解析解,并进行数值计算,将理论值与实际测量的结果进行比较.
1 理论模型及求解
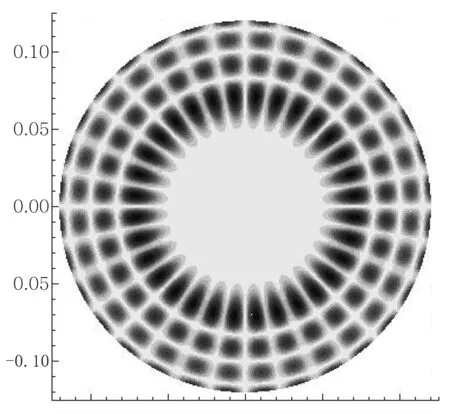
下面考虑水平放置的一块圆环形黄铜薄板,内外半径分别为a和b,其质量分布均匀,厚度为2h(h< 假定薄板的体密度为ρ,弹性模量(即杨氏模量)为Y.本文取环的圆心为坐标原点,设(x,y)点处t时刻的竖向振动小位移(小挠度)为η(x,y,t)(设静止时的位移为零),由理论声学[19]或弹性力学[21,22]方面的知识可知,在小挠度理论下η满足以下方程: (1) (2) 其中 (3) (4) 由式(2)知Z可以是方程 (5) 或方程 (6) 的解,通常应是两者的线形组合.对方程式(5)和式(6)分离变量,分别求出其通解.得方程式(2)的解的简正模式为 Z=H(r)Φ(θ)=[AJm(kr)+BYm(kr)+ CIm(kr)+DKm(kr)](Rcosmθ+Tsinmθ) (7) 其中 H(r)=AJm(kr)+BYm(kr)+CIm(kr)+DKm(kr) (8) Φ(θ)=Rcosmθ+Tsinmθ (9) Jm(kr)、Ym(kr)、Im(kr)和Km(kr)分别为m阶贝塞尔函数、m阶诺埃曼函数、第一类m阶变形(或虚宗量)贝塞尔函数和第二类m阶变形(或虚宗量)贝塞尔函数.Im(kr)和Km(kr)分别满足Im(x)=i-mJm(ix),Km(x)=(π/2)im+1[Jm(ix)+iYm(ix)],m=0,1,2,….式(8)和式(9)中的系数A、B、C、D、R、T待定.对于确定的简正频率f,若边条件确定,则式(7)中的(B/A)、(C/A)、(D/A)及k和m可完全确定下来. 若将环形薄板的内边界夹入在支体上(即固支),则满足边条件[21]: (10) (11) (12) (13) 其中 (14) (15) (16) E是薄板的抗挠刚度,E=2hρc2;对于黄铜,泊松比μ=0.324.由式(7)和式(10),得 AJm(ka)+BYm(ka)+CIm(ka)+DKm(ka)=0 (17) 由式(7)和式(11),得 (18) (19) 由式(13)、式(15)和式(16)可得 (20) 把方程式(2)的解式(7)代入式(19),得 α1(b)A+β1(b)B+γ1(b)C+δ1(b)D=0 (21) 其中 (22) (23) (24) (25) 把方程式(2)的解式(7)代入式(20),得 α2(b)A+β2(b)B+γ2(b)C+δ2(b)D=0 (26) 其中 (27) (28) (29) (30) 注意式(17)、(18)、(21)和式(26)组成关于A、B、C、D的齐次线形方程组,要使式(8)中的H(r)不恒为零,则要求该齐次线性方程组的系数行列式为零,即 (31) 式(31)决定了本征值k.而式(8)中的H(r)可表示为 (32) 显然式(32)满足式(8)所需满足的所有方程及边条件,且式(32)和式(8)可差一常数因子,该因子可并入式(9)中的系数R、T中. 河南省佛寺、道观甚多,信众数量巨大。各地佛寺、道观拥有特权,存在着严重地租剥削和高利贷剥削现象。如,在历史上的北朝佛教盛行时,寺院占有大量社会资产,僧尼享受免除租调和徭役的特权。一些大寺庙往往侵夺佃民,广占田宅。此外,佛、道教势力极大,如元代的佛教寺院经济实力雄厚,许多僧人被封有爵位,社会地位极高,连官府也不得不惧让。元初,河南洛阳白马寺住持、女真族僧人龙川被封为“扶宗宏教大师”“司空护法大师”等,并兼管江淮一带僧务;少林寺方丈福裕为元世祖钦命,死后封“晋国公”。直至20世纪50年代初,河南省内一些大寺院还有相当的产业。④ 实验时取a=4.0 cm,b=12 cm.由式(31),通过数值计算,可求出k对应于m的n个正根kmn,(n=0,1,2,…),即可解出所有可能的kmn.为了方便,对所有的kmn从小到大排列,即km0 注意kmn的单位为cm-1.可见,对m=16,若令dm=9.288 cm,则有kmndm=πβmn,βmn≈n+(m/2)-(7/2)(当n比较大时),注意这规律仅近似对m=16成立,对不同的m有不同的dm取值和βmn表达式,可见对环形薄板,并没有与圆形薄板相似的普适的克拉尼定律[9,23].表1中的底部几行分别给出了通过数值计算得到的不同频率fmn下dm的近似取值和βmn的近似表达式,并列出相应的kmn的计算结果. 表1 不同频率fmn下圆形波节线半径r的理论计算值 对于给定的m,解出所有可能的kmn后,就可根据式(3)确定容许的简谐振动的频率,即简正频率ωmn或fmn.把解出的kmn数值代回式(32),再根据式(7),即可得方程式(2)的简谐振动解的特征函数为 Zmn(r,θ)=(Rmncosmθ+Tmnsinmθ)Hmn(r) (33) 这里Z、H、R、T已加上与kmn相应的下标m、n. 令Zmn(r,θ)=0,解出的r(记为rmnl)和θ即为此频率下的圆形波节线半径及径向波节线所在的角度,其中下标l表征了r的大小.注意此时的克拉尼图形除了有若干条圆形波节线外,还可有沿r方向的2m条均匀对称的辐射状波节线.在本文的边条件下可以只有辐射状波节线(不含内边界所在的波节线)或两种波节线同时存在. 图1 频率为2.4581 kHz时的实测图(m=9,n=1) 图2 频率为6.4779 kHz时的实测图(m=17,n=1) 图3 频率为10.608 kHz时的实测图(m=16,n=3) 图4 m=16,n=3时的数值模拟图(单位:m) 下面讨论振源的影响.假定振源是集中在点(r0,θ0)以角频率ω作简谐振动的点源,则稳态运动由格林函数G给出[19],G是方程 (34) 的解.由文献[19]中的5.3.12式知,若把G按式(33)的特性函数Zmn作广义傅里叶展开,则G可表示为 (35) 总的来说,本文讨论了内边界夹入在支体上外边界悬空时环形薄铜板的二维振动解及其驻波模型:1) 振源频率很小(只有几百赫兹)时,只有径向均匀分布的波节线而没有圆形波节线(内边界所在的波节线除外).2)当振源频率达到并超过某一适当频率后,一般情况下,m≠0,两种类型的波节线(包括圆形和辐射状)通常都同时存在.无论哪种情况,只要振源位置及频率确定(其中频率可精细调节),则波节线位置和数目就可以完全确定下来,还可发现实验值跟理论值相当符合.由于薄板所受重力、内摩檫力、板的不均匀性及细沙质量等因素没有考虑,而在有些频率下某一半径附近的振幅可能都很小,也会导致细沙的聚集,故部分圆形波节线的半径的实验值跟理论值稍微有些不同.用本文之方法确定式(3)中的常数c,以及式(34)中的kmn之取值,即可求出容许的共振频率ωmn(或fmn),其中最低共振频率f00最为重要.因为共振现象在很多振动系统中(比如汽车之板件、飞机之机翼、大楼之楼盖等)比较危险,容易对这些系统造成结构破坏或断裂.故为了安全起见需在设计时就避开这些共振频率. [1] Chladni E F F.Entdeckungen über die Theory des Klanges,Breitkopf und Härtel [M].Leipzig,1787. [2]Hawkes J J,Radel S.Acoustofluidics 22:Multi-wavelength resonators,applications and considerations [J].Lab on a Chip,2013,13:610-627. [3]Ochs J B,Snowdon J C.Transmissibility across simply supported thin plates.II.Rectangular plates with loading masses and straight ribs [J] .The Journal of the Acoustical Society of America,1976,59:350-354. [4] Hodges C H,Woodhouse J.Theories of noise and vibration tra- nsmission in complex structures [J] .Reports on Progress in Physics,1986,49:107-170. [5] Dorrestijn M,Bietsch A,Acikalin T,et al.Chladni Figures Revisited Based on Nanomechanics [J] .Physical Review Letters,2007,98:026102. [6]Stein J,Stöckmann H-J.Experimental Determination of Billiard Wave Functions [J] .Physical Review Letters,1992,68:2867-2870. [7]Thomas B, and Squires A M. Support for Faraday’s view of Circulation in a Fine-Powder Chladni Heap[J].Physical Review Letters,1998,81:574-577. [8]Proefschrift.Newton vs Stokes:Competing Forces in Granu- lar Matter [M].Henk Jan van Gerner,Enschede,The Netherlands,2009. [9]RayleighL.The Theory of Sound (Vol.I) (2st Ed.revised and enlarged) [M].New York:Dover Publication,1945:358-363. [10]宋力,张平.关于弹性地基上圆环形薄板振动问题的解答(续一) [J] .沈阳工业学院学报,1996,15(1):85-94. [11]宋力,张景异.关于弹性地基上圆环形薄板振动问题的解答.金属成型工艺 [J].1997,15(4):34-38. [12]吴伟,宋力.弹性地基上圆环形薄板振动问题的研究 [J].沈阳工业学院学报,1997,16(3):46-50. [13]方奕忠,王钢,沈韩,等.方形薄板二维驻波的研究 [J] .物理实验,2014,34(1):33-36. [14]方奕忠,王钢,沈韩,等.圆形薄板二维驻波的研究 [J] .大学物理,2015,34(3):19-24. [15]黄炎.矩形薄板弹性振动的一般解析解 [J].应用数学和力学,1988,9(11):993-1000. [16]Chladni patterns in vibrated plates[EB/OL].http://www.physics.utoronto.ca/nonlinear/chladni.html. 2013-12-1. [17]李文深.圆形薄板的振动 [J].黑龙江大学自然科学学报,1991,8(1):47-50. [18]许琪搂,王仁义,常少英.四边支承矩形板自由振动的精确解法 [J].郑州工业大学学报,2001,22(1):1-5. [19]莫尔斯 P M,英格特 K U.理论声学:上册 [M].吕如榆,杨训仁,译.北京:科学出版社,1984:252-257. [20]王龙甫.弹性理论 [M].北京:科学出版社,1978:357-360. [21]钱伟长,叶开源.弹性力学 [M].北京:科学出版社,1956:285-286. [22]朗道 L D,栗弗席兹 E M.弹性理论[M].5版.武际可,刘寄星,译.北京:高等教育出版社.2011:115-116. [23]Rossing T D.Chladni’s law for vibrating plates [J] .American Journal of Physics,1982,50:271-274. Two-dimensional standing waves on annular plate as the inner boundary being cramped FANG Yi-zhong, SHEN Han, WANG Gang, CUI Xin-tu, LIAO De-ju, FENG Rao-hui (School of Physics, SunYat-sen University, Guangzhou, Guangdong 510275, China) The two-dimensional standing wave figures of an annular plate (Chladni patterns) as the inner boundary is clamped, are investigated experimentally and theoretically. It is found that the Chladni patterns can be precisely controlled by adjusting the frequency and position of the vibration source. Two kinds of patterns have been observed, one kind only has radial nodal lines (excepting the inner boundary) and the other has both of radial nodal lines and circular nodal lines. Furthermore, the radii of the circular nodal lines, the change rules of the eigen values, and the elastic modulus of the thin plate have been obtained. The results of experiments are consistent with the analytical solutions. standing waves;m-order Bessel functions; Chladni figures; annular plate 2015-05-26: 2015-12-07 国家自然科学基金资助项目(11175268)、中山大学实验教学研究(改革)基金项目(YJ201109)资助 方奕忠(1969—),男,广东开平人,中山大学物理学院工程师,博士,主要从事大学物理实验教学与研究工作. 物理实验 O 347.4+2; O4-33 A 1000- 0712(2016)06- 0015- 06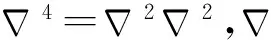

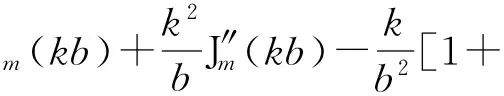
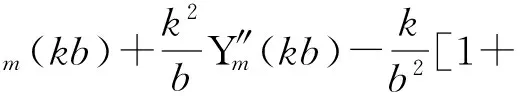
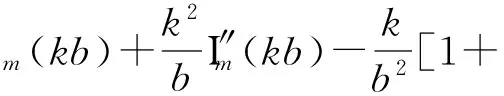

2 理论值与实验结果对比






3 进一步的分析与结论