磁控法测量热发射电子速率分布的理论研究
周 越
(北京林业大学 理学院,北京 100083)
磁控法测量热发射电子速率分布的理论研究
周越
(北京林业大学 理学院,北京100083)
指出在磁控法测量热发射电子速率分布实验中,结果应为电子径向速率的分布,并证明电子的径向速率符合麦克斯韦速率分布率.
热电子发射;磁控管;速率分布率
按照统计理论,热发射电子的速率分布不同于麦克斯韦速率分布. 为了验证这一规律,在文献[1]中设计了利用磁控管测量热发射电子速率分布的实验,通过测量不同励磁电流下的阳极电流来获取电子速率分布的信息,但实验结果在定量上和理论值存在比较明显的差异. 本文对该实验进行了理论分析,说明在实验中测得的分布实际是电子沿真空二极管径向速率的分布,其理论分布为麦克斯韦速率分布.
1 实验概述
磁控管本质上说是一个置于螺线管内的真空二极管. 用通电的方式给真空二极管中心作为阴极的钨丝加热,钨丝中部分电子获得足够的能量后会逸出金属表面产生热电子发射,发射出的电子被圆筒形的阳极收集形成阳极电流Ia.如在螺线管上加载励磁电流Is,会产生沿真空二极管轴向的磁场,从阴极飞向阳极的电子将在洛伦兹力的作用下做匀速率圆周运动,从而有返回阴极的倾向. 如果电子做圆周运动的半径小于真空二极管阳极半径的一半,将无法到达阳极. 可以证明电子的临界速率正比于螺线管中的励磁电流,即vc=KIs. 逐步增大励磁电流,因发射速率低于vc而无法到达阳极的电子越来越多,阳极电流相应递减,这样就可以通过测量阳极电流的大小获得电子速率分布的信息. 将Is=0时的阳极电流记为Ia0,Is=Isi时的临界速率和阳极电流分别记为vci和Iai. 因阳极电流和单位时间抵达阳极的电子数成正比,且Iai完全来自于速率大于vci的电子的贡献,故(Ia0-Iai)/Ia0等于电子速率的累积分布,即速率小于vci的电子所占比例.
2 对实验结果的讨论
根据统计理论,热发射电子的速率分布为[2]
(1)
g(u)du=2u3e-u2du
(2)
相应的累积分布函数为

(3)
在文献[1]中通过测量(Ia0-Iai)/Ia0绘出了φ(u)的曲线,实验结果和式(3)给出的理论值定性符合,但在定量上仍存在比较明显的偏离. 具体表现在φ(u)的实验值上升速度比理论值要快,这提示实测的电子最概然速率比理论预言的要小.
另外,对式(3)做幂级数展开可得当u<<1时有φ(u)∝u4.为了验证这一关系,在文献[1]中还绘制了lnφ(u)-lnu图. 理论上说lnu越小,lnφ(u)-lnu图像的斜率越趋近于4,而实验数据中与这个关系符合度较好的区域更接近曲线的中段,且在u~0的邻域数据点偏少,由此断言4次方规律得到验证是值得商榷的.
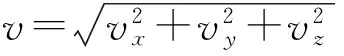
3 电子速率分布的推导

(4)

(5)
电子要逸出金属表面需克服高为Eb的表面势垒,根据逸出功的定义[4]
A=Eb-εF
(6)
因此热发射电子在金属内部的能量需要比费米能级高A以上,一般为几个eV. 而阴极的典型工作温度在2000 K左右,在此条件下满足E-εF>>kT,费米-狄拉克分布过渡到玻尔兹曼分布,故可将式(5)近似表示为
(7)
如阴极发射的电子在真空中的动量为(px,py,pz),则有
(8)
将以上关系代入式(7),并利用式(6),可得
(9)
从式(9)出发可以导出电子的不同速率分布,分述如下.
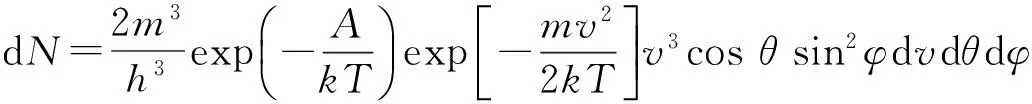
(10)
对θ和φ积分可得速率在[v,v+dv]区间内的电子数为
(11)
再对v积分可得
(12)
N为单位时间通过单位表面积逸出的电子总数. 将式(11)和式(12)相除可得v的分布
(13)
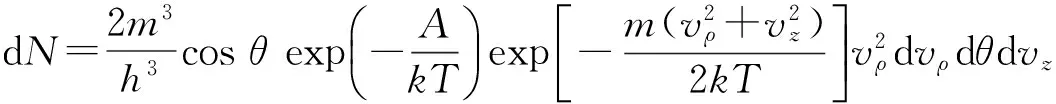
(14)
对θ和vz积分可得径向速率在(vρ,vρ+dvρ)区间内的电子数为
(15)
将式(15)和式(12)相除,即可得到vρ的分布
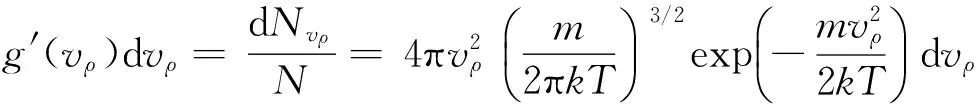
(16)

4 和实验值的比较
仍采用约化速率将式(16)改写为简洁形式
(17)
其累积分布函数可以用高斯误差函数表示为
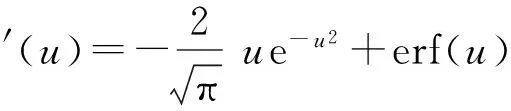
(18)
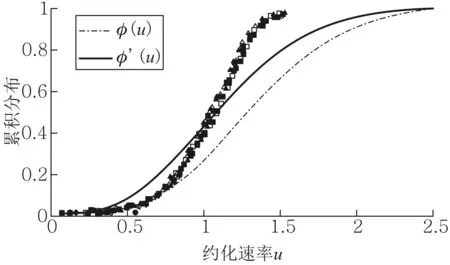
图1 电子速率累积分布函数与约化速率的关系.点横线和实线分别表示φ(u)和φ′(u), 离散点为文献[1]中的实验值
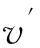
在施加强磁场的情况下,电子因做曲线运动在两极之间停留时间增加,空间电荷效应更为明显. 结果是,磁场未达到预计强度时就可以将阳极电流Iai近乎截止,阳极电流下降速度比理论要快. 相应地,实验曲线(Ia0-Iai)/Ia0在高速区域(对应于所加磁场较强的区域)比理论更快地趋于1.
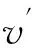
5 对进一步实验的建议
如前所述,空间电荷效应对实验结果在定量上存在明显影响,设法将其减弱或消除有助于提高实验精度. 如果给真空二极管加一正向偏置,将使阴阳极之间的电势最低点向阴极方向移动. 当正向偏置电压足够强时,两极之间不再存在电势最低点,这样就不会出现低速电子被势垒阻挡的问题. 不过,施加偏置后电子的临界速率和励磁电流是相对复杂的非线性关系.
另外,在文献[1]中只测出了累积分布函数φ(u)的曲线,而未对g(u)测量. 根据临界速率和励磁电流的关系,只要令励磁电流Is每次增加适当的幅度即可将热发射电子按相等的速率间隔分开;通过测(Iai-Iai+1)/Ia0可以获得每个速率间隔内电子的相对比例. 因此,利用磁控管的测量数据画出g(u)的图像是可行的,这样有利于更完整地展示热发射电子的速率分布规律并与理论值相对比.
[1]侯吉旋, 司黎明. 磁控法测定热发射电子的速率分布 [J]. 大学物理, 2014, 33(12): 21-22.
[2]付慈海, 杨英杰. 物理电子技术原理 [M]. 广州: 华南理工大学出版社, 1991: 79.
[3]薛增泉, 吴全德. 电子发射与电子能谱 [M]. 北京: 北京大学出版社, 1993: 41-42, 50-52.
[4] 姚宗熙, 郑德修, 封学民. 物理电子学 [M]. 西安: 西安交通大学出版社, 1991: 59.
A theoretical research for measuring the velocity distribution of thermionic electrons with magnetron
ZHOU Yue
(College of Science, Beijing Forestry University, Beijing 100083)
It is pointed out that the result should be distribution of radial velocity in the experiment of the velocity distribution of thermionic electrons with magnetron. It is proved that the radial velocity distribution of thermionic electrons accords with the Maxwell velocity distribution.
thermionic electron emission; magnetron; velocity distribution
2015-02-12;
2015-11-06
中央高校基本科研业务费专项资金(TD2014-04)资助
周越(1982—),男,北京人,北京林业大学理学院讲师,博士,主要从事普通物理和电子学教学与研究工作.
O 441.5
A
1000- 0712(2016)06- 0033- 03

