Mathematica在高等数学中的简单应用

陈静

【摘要】讨论了利用Mathematica软件画图求极限以及单调性等，并用此软件进行计算.

【关键词】Mathematica;高等数学;画图;计算

高等数学是高等教育阶段一门重要的基础课，但由于其知识点多，逻辑性强，计算量大，抽象性高，不少同学觉得高等数学空洞、枯燥、乏味.为了增强同学们学习高等数学的兴趣，平时教学过程中结合现代信息技术教学，已成为一个必然趋势.而Mathematica软件使用简单，功能强大，借助它可以使课程更加形象化、生动化.

一、借助Mathematica软件画图解决问题

1.在极限中的应用

利用极限的定义来求极限的关键是先要画出函数的图像，对于画一些稍微复杂的函数的图像，我们就可以借助Mathematica软件来解决.

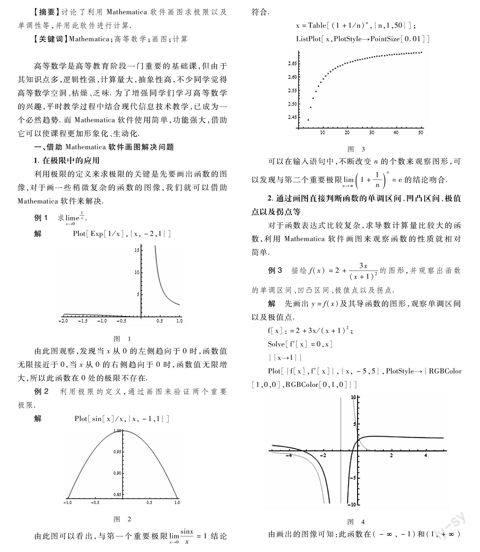
例1 求limx→0e1x.

解 Plot[Exp[1/x]，{x，-2，1}]

图 1

由此图观察，发现当x从0的左侧趋向于0时，函数值无限接近于0，当x从0的右侧趋向于0时，函数值无限增大，所以此函数在0处的极限不存在.

例2 利用极限的定义，通过画图来验证两个重要极限.

解 Plot[sin[x]/x，{x，-1，1}]

图 2

由此图可以看出，与第一个重要极限limx→0sinxx=1结论符合.

x=Table[（1+1/n）n，{n，1，50}];

ListPlot[x，PlotStyle→PointSize[0.01]]

图 3

可以在输入语句中，不断改变n的个数来观察图形，可以发现与第二个重要极限limn→∞1+1nn=e的结论吻合.

2.通过画图直接判断函数的单调区间、凹凸区间、极值点以及拐点等

对于函数表达式比较复杂，求导数计算量比较大的函数，利用Mathematica软件画图来观察函数的性质就相对简单.

例3 描绘f（x）=2+3x（x+1）2的图形，并观察出函数的单调区间、凹凸区间、极值点以及拐点.

解 先画出y=f（x）及其导函数的图形，观察单调区间以及极值点.

f[x]：=2+3x/（x+1）2;

Solve[f′[x]=0，x]

{{x→1}}

Plot[{f[x]，f′[x]}，{x，-5，5}，PlotStyle→{RGBColor[1，0，0]，RGBColor[0，1，0]}]

图 4

由画出的图像可知：此函数在（-∞，-1）和（1，+∞）上单调递减，在（-1，1）上单调递增;x=1为极大值点.

再画出y=f（x）及其二阶导函数的图形，观察其凹凸区间和拐点.

f[x_]：=2+3x（x+1）^2;

g[x_]=D[f[x]，{x，2}]

18x（1+x）4-12（1+x）3

Slove[g[x]=0，x]

{{x→2}}

Plot[{f[x]，g[x]}，{x，-5，5}，PlotStyle→{RGBColor[1，0，0]，RGBColor[0，0，1]}]

图 5

此函数在（-∞，-1）和（-1，2）上是凸的，在（2，+∞）上是凹的;拐点是x=2.

二、利用Mathematica软件计算，提高解题速度

1.求极限

Limit[f[x]，x->x0];

Limit[f[x]，x->x0，Direction->-1];Limit[f[x]，x->x0，Direction->1].

上述三个命令分别表示求函数在x0处的极限、左极限和右极限.

例4 求limx→∞sinxx2-π2.

解 ln[3]：=Limitsin[x]x2-π2，x→π

Out[3]=-12π

2.求导数

D[f[x]，x]——求函数的导数;D[f[x]，{x，n}]——求函数的n阶导数.

例5 求y=（1+cosx）1x的导数.

解 ln[4]：=D[（1+cos[x]）1x，x]

Out[4]=（1+cos[x]）1x-log[1-cos[x]]x2-sin[x]x（1+cos[x]）

3.求极小值

FindMinimum[f[x]，{x，x0}]——求函数在点x0附近的极小值.

例6 求函数f（x）=x3（6x+7）2的极小值.

解 ln[6]：=FindMinimum[x3（6x+7）2，{x，-1}]

Out[6]={-1.3906，{x→-0.7}}

即：在x=-0.7处取得极小值-1.3906.

4.求积分

Integrate[f[x]，x]——计算不定积分∫f（x）dx;

Integrate[f[x]，{x，a，b}]——计算定积分∫baf（x）dx.

例7 求解不定积分∫sin（lnx）dx.

解 ln[1]：=Integrate[sin[log[x]]，x]

Out[1]=-12xcos[log[x]]-12xsin[log[x]]

5.求微分方程

DSolve[方程，y，x]——求以x为自变量的方程的解;

DSolve[{方程1，方程2，…}，y，{x，xmin，xmax}]——求函数y的数值解，x属于[xmin，xmax];

DSolve[{方程1，方程2，…}，{y1，y2，…}，{x，xmin，xmax}]——求多个函数yi的数值解.

例8 求微分方程y″-2y′+5y=exsin2x的通解.

解 ln[1]：=DSolve[y″[x]-2y′[x]+5y[x]==ex*sin[x]，y[x]，x]

Out[1]={{y[x]-exC[2]cos[2x]+exC[1]sin[2x]-112ex（4cos[2x]sin[x]3-3cos[x]sin[2x]+cos[3x]sin[2x]）}}

Mathematica软件具有强大的计算功能，便捷的使用方法，在高等数学中使用广泛，具有很强的应用性.在高等数学的教学中穿插Mathematica软件的学习，可以提高学生的学习兴趣，培养学生会用数学知识，借助计算机，提高分析和计算应用问题的能力.

【参考文献】

[1]汪晓虹.高等数学实验——学软件 做数学[M].北京：国防工业出版社，2010.

[2]蔡俊娟.Mathematica在高等数学教学中的应用[J].长江大学学报（自然科学版），2009（4）：346-348.

[3]纪宏伟，苏莹，高金新.Mathematica在高等数学中的典型问题应用探索[J].贵州师院学院学报，2011（3）：20-23.

[4]曹瑞成，姜海勤.高等数学[M].北京：化学工业出版社，2007.