“语文文体”模型与计算题模型

何孟福 练海元

我们的物理教学应该是“去问题化”教学向“生问题化”教学转變。课堂的中心，应该是一个问题的提出、理解及解决并产生新问题的过程，是一个知识——作为问题解决的工具被探索、被发现的过程。优秀的课堂物理课堂教学，培养学生“深度学习”构建物理模型，通过课堂教学培养学生学会学习，培养学生从问题中明理，明理中重现新的问题这一神奇的创造过程。如果问题枯竭了，课堂也就死去了。我们课题组深刻领会教学的内涵，培养学生处理问题的能力，把物理计算题模型与语文文体模型有机结合起来，为学生更好的解决问题提供思路。

1、物理计算题的题目结构示意图

例如：如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径，P点到桌面的竖直距离也是R。用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放，物块过B点后其位移与时间的关系为，物块飞离桌面后由P点沿切线落入圆轨道。g=10m/s2，求

（1）BP间的水平距离。

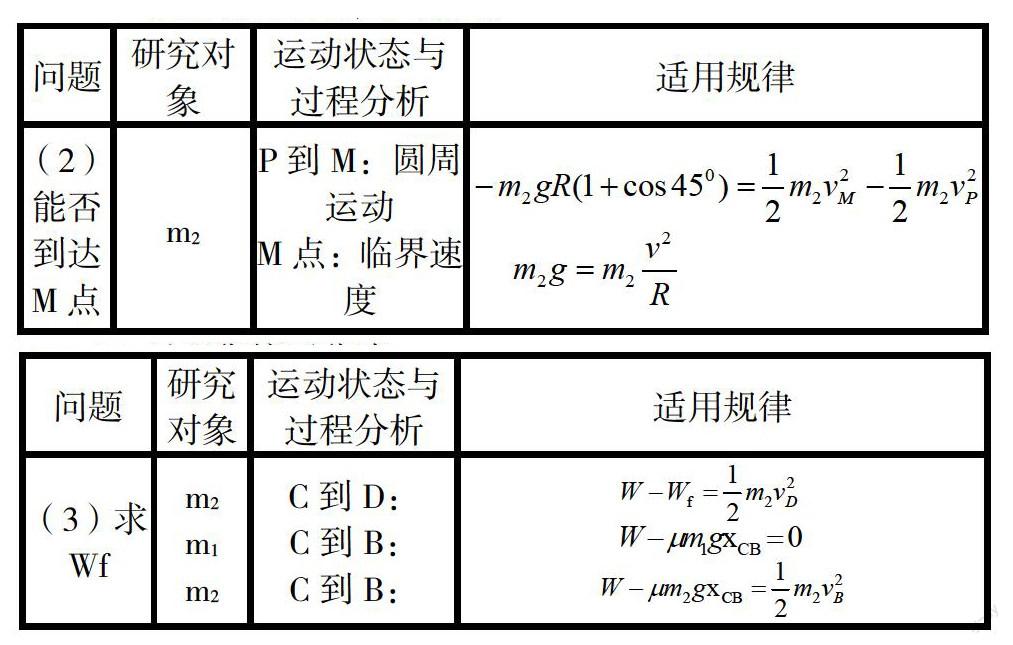
（2）判断m2能否沿圆轨道到达M点。

（3）释放后m2运动过程中克服摩擦力做的功

1.1“说明文”部分：如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径，P点到桌面的竖直距离也是R。

1.2“记叙文”部分：用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放，物块过B点后其位移与时间的关系为，物块飞离桌面后由P点沿切线落入圆轨道。

1.3“议论文”部分：求（1）BP间的水平距离。（2）判断m2能否沿圆轨道到达M点。（3）释放后m2运动过程中克服摩擦力做的功

2、物理计算题读题策略

正如干国祥所说：“课堂，是真理呈现之处；教学，是知识散发出魅力之时。在静态的教材下面，蕴藏着人类最伟大的奥秘：发现问题，梳理整个物理过程。课堂教学，是这一发现与梳理的重温，是这一发现与梳理的延续。而如果没有将“问题-知识-真理”作为课堂教学的核心，那么，一切的热闹都将是浅薄而不值一提的。”

2.1把说明具体形象化

把说明部分物理量标注在右图的草图上，化文字描述为图象直观，然后再针对草图复述说明与题目对比，达到防止遗漏.

2.2把记叙部分过程化

过程一、用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点。

过程二、用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放，物块过B点后其位移与时间的关系为，过程三、物块飞离桌面后由P点沿切线落入圆轨道。

2.3把议论部分论证具体化

论点一、BP间的水平距离。由三个物理过程C到B过程 ；B到D过程；D到P过程。此论点涉及到主要的“运动情况”。对运动情况分析应该立足于受力分析。

论点二、判断m2能否沿圆轨道到达M点。该论点涉及竖直面的“类轻绳”运动模型。对此轻绳与类轻绳问题，应该立足于“临界状态分析”

论点三、释放后m2运动过程中克服摩擦力做的功：该论点涉及的是变力做功问题：该论点阐述应该立足于“变力功的模型求解法”

3、计算题的表述模式

3.1过程语言犀利陈述，过程如下

解题——规范解答：文字规范：简练指明对象、状态、过程；作图规范：线条清晰、直观准确；列式规范：能符合物理公式的基本形式；符号规范：按题设符号和规范符号书写；单位规范：数值结果应有单位；答案规范：最终结论应与题设问题相契合

整理解题流程，确定书写顺序

3.2状态特征明确，原理清晰

3.3过程衔接要分清

从语文角度来说，文体不仅在于作者写出了多少，更在于读者针对作者陈述内容明理了多少；教育也不在于教师讲出多少，更在于学生悟出多少。教师讲得再多，也还是教师的，学生就算是理解了，但这种被动的理解，真的就那么重要吗？而学生哪怕“悟”得再少，但也是自己的，是自己成功的体验和收获。这里的“悟”，应该是情景中的内化和建构，任何高明的教师也不可能代替学生这个生成过程。唯有这样的生成过程，才是教育的本意所在，也是人的成长所在，拔节所在，升华所在。