“四策略”助力小学低段学生几何直观培养
徐玉钗
【摘要】几何直观作为2011年版《数学课程标准》十大核心概念之一,它的重要性不言而喻.学生几何直观培养是一个循序渐进的过程.经过实践,笔者认为激发“兴趣”,引发学生“需要”;指导“画图”,形成正确“表征”;关注“差异”,促进互助“成长”;有效“训练”,增强应用“意识”;这“四策略”能让低年级学生在潜移默化中感受到几何直观的价值,形成几何直观的意识,并逐步培养几何直观的思维方式与能力.
【关键词】低段学生;几何直观;四策略
2011年版《数学课程标准》明确指出:“几何直观主要是指利用图形描述和分析问题.借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果.”可见,几何直观不仅是教师数学教学的有效策略,而且是学生学习数学的重要能力与思维方式,它影响着学生数学学习的整个过程.那么,针对小学低年级学生,如何培养他们的几何直观呢?笔者认为,就如教育时机一样,遵循低年级学生的心理特点,运用“四策略”,能够卓有成效地培养学生的几何直观.
一、激发“兴趣”,引发学生“需要”
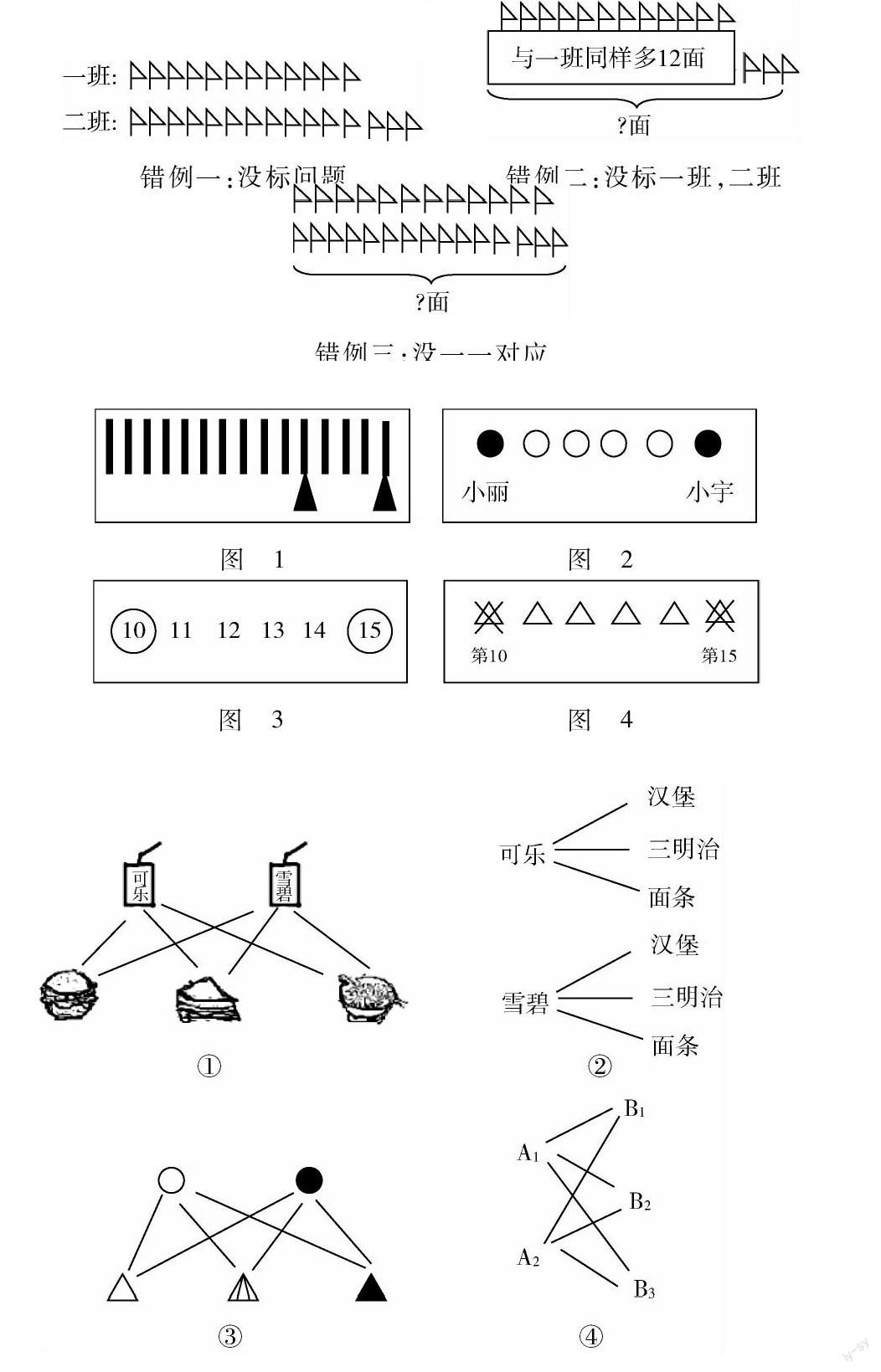
建构主义学习理论认为,学生的数学学习过程是一个自主建构的过程.教学时,教师如果善于激发学生的“兴趣”,就能让学生在学习过程中产生强烈的好奇心和求知欲.因此,当学生在解决问题遇到困难时,正是激发学生运用几何直观的最佳时机.在解决新人教版一上P79例6“小丽说:我排在第10个,小宇说:我排在第15人,小丽和小宇之间有几人?”这个问题时,很多孩子收集完信息,就迫不及待宣布结果:“5人”,师问:“你怎么想的?”大部分孩子想都没想骄傲地回答“15-10=5(人)”,笔者没有马上评价,而是追问:“有不同答案吗?”几秒钟的停顿后,有了不同的声音“4人”,当孩子们争论不休时,教师故显无可奈何:“这样争论不是办法啊?谁也说服不了谁.”一聪明的孩子提议到:“我们可以画图来看就明白了.”一石激起千层浪,孩子们兴趣高涨,激动地附和到:“对哦,画图就很清楚了.”以下是部分孩子画的图示:
图1
图2
图3
图4
虽然,孩子们的图式各不相同,但从图上我们看到孩子的思维,他们借助“几何直观”这一分析的拐杖,不仅成功的解决了问题,而且直观的理解了15-10=5错误的原因.在教学中,教师注意激发学生“画图思考”的兴趣,比卖力的强调与推销让学生被动接受效果好得多.
二、指导“画图”,形成正确“表征”
几何直观的培养不是一蹴而就的,而是需要一个过程.低年级学生首先要学会正确地用图表征加法、减法、乘法、除法的意义,到了中高年级才能更好地借助几何直观来理解数学.因此,教给低年级学生一些基本的画图技巧尤为重要.笔者认为,在学生产生画图欲望后,教师可根据学生实际适时指导画图.指导学生画图的方法很多,而针对低年级学生的特点,我们教学过程要注意细节的“放”,先让学生自主尝试,再利用课堂生成的“错误”资源,让学生在争辩中,学会“图式”的正确“表征”.如新人教版二上P23例4“求比一个数多几的数”,学生产生画图需要后,先根据信息独立尝试画图,接着在集体讨论环节中,笔者不失时机的展示收集来的小“缺憾”的学生作品,如:
错例一:没标问题
错例二:没标一班,二班
錯例三:没一一对应
在一一展示中,学生积极“找茬”,课堂顿时活跃了起来,学生思维碰撞,建立了“求比一个数多几的数”图式的正确表征.如此指导画图,改变了原来教师示范,学生无趣接受,为“小老师”互相启发,学生主动调整,自我完善的过程,学生参与度高,效果更好.哲学家波普尔曾说过:“错误中往往孕育着比正确更丰富的发现和创造因素,发现的方法就是试错的方法.”教师引导学生主动实现由最初的“随意尝试画图”向后期“正确图式表征”转变.引导他们经历“利用图形描述和分析问题”的酸甜苦辣体验,不仅积累了画图经验,更是建立了与几何直观的深厚情感.
三、关注“差异”,促进互助“成长”
“世界上没有完全相同的两片叶子”.可见,差异是必然存在的.同一年龄,同一年级的学生所体现的几何直观水平也不尽相同.针对差异,2011版《小学课程标准》特别提出这样的理念:不同的人在数学上得到不同的发展.笔者认为,当我们把学生的个体“差异”当作资源,而不是“嫌弃”,不仅能让每名学生的几何直观在原有水平上有所提高,而且能在学生互助分享中,促进整体几何直观的发展.在新人教版三下P102“搭配中的学问”教学时,笔者创设了一个饮食店促销活动的广告情境,买一份饮料和一份主食可以享受半价,并在广告单上显示了三种主食图片(面条、三明治、汉堡),两种饮料图片(可乐、雪碧),问“如果要享受半价,共有几种不同的搭配?”在具体分析问题时,“画图思考”成了学生首选的策略,如图:
从展示出来不同的图式中,我们看到学生不同的几何直观水平,有“实物直观”、“图形直观”、“简约符号直观”、“替代物直观”.针对学生“有差异”的图式,笔者引导学生对比(实物图连线法,图形连线法、字母连线法)提出质疑:“你喜欢哪种图式,为什么?”学生争先恐后地回答:“我喜欢第四个,因为它最简洁”.这样的比较、感悟是一种无声的引导,在后面的练习中,学生都自觉的采用更高层次的直观表现形式.接着再引导学生类比,发现这些图式背后隐藏着共同的有序搭配的本质,从而成功地总结出“2×3=6(种)”,能用乘法原理解决的高度.荷兰教育家弗赖登塔尔说:教师的作用就是如何使每一名学生达到尽可能高的水平.笔者认为,“差异”的有效利用,也是发展学生几何直观的策略之一.
四、有效“训练”,增强应用“意识”
对于学生来说,几何直观不仅是一种技能、能力,更是一种思维方式.在低年级我们不仅要帮助学生掌握一定的几何直观的画图技巧,更重要的是让学生形成“画图思考”的几何直观意识.如:新人教版一下P12的“数学思考”中会遇到这样的问题:我们一队有10个男生,老师让我们相邻两个男生之间插进一个女生.一共可以插进多少个女生?通过“画图试试”就能很快知道女生与男生人数的关系,不仅能让学生很快寻找到问题的答案,而且能帮助学生更好的理解抽象的算式10-1=9(人),又如排队问题:在一个队伍中,小东排在从前往后数第9个,从后往前数第7个,他所在的这个队伍有多少人?教材类似这样的资源还有很多.教学中,教师遵循低年级学生的心理特点,有效进行“画图思考”的训练,让学生在扎实、有效的几何直观实践中历练,积累丰富的几何直观经验,让学生形成“画图思考”的几何直观应用意识,从而逐渐形成几何直观的能力.
万丈高楼平地起,低年级学生几何直观的渗透与培养至关重要.教学中,教师根据学生的心理特点,让“巧妙的教学细节处理”彰显神奇的力量,有效地培养学生“画图思辨”的几何直观意识.就如数学教育家弗莱登塔尔所说:“几何直观能告诉我们什么是可能重要、可能有意义和可接近的,并使我们在课题、概念与方法的荒漠之中免于陷入歧途之苦.”虽然学生几何直观的培养是一个长期的过程,但是相信这样的开始是良好的开端.
【参考文献】
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012:6.
[2]孔凡哲.史宁中.关于几何直观的含义与表现形式——对《义务教育数学课程标准(2011年版)》的一点认识[J].课程教材教法,2012(7).
[3]秦德生.关于几何直观的思考[J].中小学数学教学参考,2005(10).
[4]蔡宏圣.几何直观:小学数学教学的视角[J].课程·教材·教法,2013(5).