基于二进制算法验算哥德巴赫猜想

周佳盛 孙文文

【摘要】本文阐述的结果成立是哥德巴赫猜想猜想成立的必要条件，利用了二进制数简单的表达方式，从二进制数的角度去验算哥德巴赫猜想.

【关键词】二进制；哥德巴赫猜想

一、绪论

1.二进制定义

二进制是计算技术中广泛采用的一种数制.二进制数据是用0和1两个数码来表示的数.它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”，由18世纪德国数理哲学大师莱布尼兹发现.

第三次科技革命的重要标志之一的计算机的发明与应用，因为数字计算机只能识别和处理由‘0.‘1符号串组成的代码.其运算模式正是二进制.19世纪爱尔兰逻辑学家乔治布尔对逻辑命题的思考过程转化为对符号“0”.“1”的某种代数演算，二进制是逢2进位的进位制.0、1是基本算符.因为它只使用0、1两个数字符号，非常简单方便，易于用电子方式实现.

2.哥德巴赫猜想介绍

提出者：德国教师哥德巴赫.

提出时间：1742年.

内容表述：素数又称质数，它是只能被1和此数本身整除的整數.素数数列中，仅2为偶数，其余均为奇数.

任何一个大于2的偶数，都可以表达为两个素数之和.

若设x，y均为素数，z为大予2的偶数，则哥德巴猜想可表达为：z=y+x.

3.国内外研究状况

1937年，苏联数学家伊万·维诺格拉多夫更进一步，在无需广义黎曼猜想的情形下，直接证明了充分大的奇数可以表示为三个素数之和，被称为“三素数定理”.不过他无法给出“充分大”的界限.他的学生博罗兹金于1939年确定了一个“充分大”的下限：314348907.这个数字有6846169位，要验证比该数小的所有数完全不可行.

1995年，法国数学家奥利维耶·拉马雷证明，不小于4的偶数都可以表示为最多六个素数之和.莱塞克·卡涅茨基证明了在黎曼猜想成立的前提下，奇数都可表示为最多五个素数之和.2012年，陶哲轩在无需黎曼猜想的情形下证明了这一结论.

二、方法介绍

1.理论基础

（1）二进制加法法则

在二进制原码的加法中，两个任意的n位二进制数相加不能得到一个n+2的二进制数.

例1已知四位二进制数c=1000，是否能够由两个二位二进制数a和b相加所得该四位二进制数.

答：否，设两个a与b皆为11，则相加为110.因为此时a+b为最大值，则命题不成立.

（2）奇数偶数在二进制中的表示

与十进制不同，在二进制中的偶数和奇数唯一的不同点在于末尾的数字.

末尾数字为‘1时（即20），则为奇数，数字‘0则为偶数.

例1二进制数10001的十进制表示为17，为奇数

二进制数10000的十进制表示为16，为偶数

由此可见，在的多数情况下相邻的奇数与偶数，在二进制中的差异是末尾数字的不同.又因为两个奇数相加必然是偶数，两个素数（不考虑素数2）相加必然是偶数.

因此在之后的运算中，为了方便运算，我们将不看末尾，即把所有的偶数和奇数合在一起看.

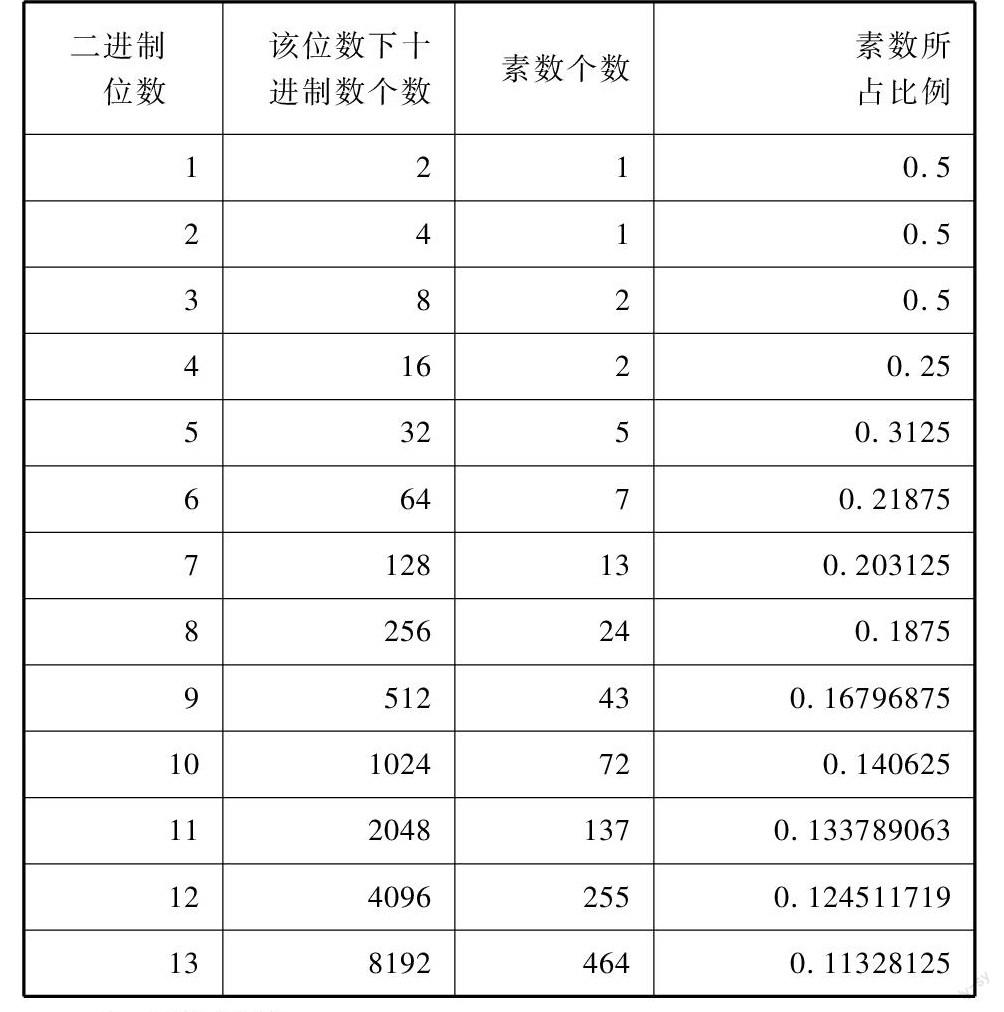
（1）素数在二进制数中的表示

二进制位数[]该位数下十进制数个数[]素数个数[]素数所占比例

1[]2[]1[]0.5

2[]4[]1[]0.5

3[]8[]2[]0.5

4[]16[]2[]0.25

5[]32[]5[]0.3125

6[]64[]7[]0.21875

7[]128[]13[]0.203125

8[]256[]24[]0.1875

9[]512[]43[]0.16796875

10[]1024[]72[]0.140625

11[]2048[]137[]0.133789063

12[]4096[]255[]0.124511719

13[]8192[]464[]0.11328125

3.方法阐述

从二进制加法法则可知，当n位二进制数与n+2位二进制数间没有素数出现存在时，哥德巴赫猜想则不成立.

但是该方法不能证明当n位二进制数与n+2位二进制数间没有素数出现存在时，哥德巴赫猜想一定成立.

4.猜想与展望

从上表可知在一个二进制位数上的素数个数是有递增的趋势，且占比有递减趋势.虽然素数在二进制数位上的个数所占比例会随着二进制位数的递增而递减，但是素数个数却依然在增加，因此可以通过此方法证明或者推翻哥德巴赫猜想.

【参考文献】

[1]数学史上的五大趣味难题（N）.生活文摘报，2007-03-02（9）.

[2]基于哥德巴赫猜想的猜想和联想，古工（A）.