浅谈平面向量数量积求解的几种途径

魏智琴

【摘要】平面向量数量积是平面向量一章中的重要内容，是高中数学三角函数、平面几何、解析几何等章节知识的交汇点，也是高考重点考查的知识，许多学生在解此类题时感觉困难，究其原因，就是学生对数量积的概念理解不透彻，下面就求解方法归纳如下.

【关键词】平面向量；数量积；求解方法

一、定义法

从定义来看求两个非零向量的数量积关键要弄清楚两向量的模和夹角；若从数量积的几何意义来看就是一向量的模与它在另一向量方向上的投影的乘积.

例1（1）在△ABC中，a=5，b=8，C=π3，则BC·CA=.

（2）已知圆O：x2+y2=4，直线l：x-3y+3=0与圆O交与A，B两点，则OA·OB=.

解（1）如图1，在△ABC中，BC·CA=BCCAcos（π-C）=5×8×-12=-20.

图1

（2）如图2，过点O作OC垂直于AB于点C，由点到直线的距离公式可得OC=310，在Rt△OAC中，cos∠AOC=3210，则cos∠AOB=2cos2∠AOC-1=2×32102-1=-1120，从而OA·OB=OA·OBcos∠AOB=2×2×-1120=-115.

图2

二、坐标法

设a=（x1，y1），b=（x2，y2），则a·b=x1x2+y1y2.用此方法解决向量数量积问题，必须先建立合适的平面坐标系，把向量坐标化.

例2（1）如图3，在等腰直角三角形ABC中，AC=BC=1，点M，N分别是AB，BC的中點，点P是△ABC（包括边界）内任一点.则AN·MP的取值范围为.

图3

（2）如图4，在ABCD中，已知AB=2，AD=1，∠DAB=60°，点M为AB的中点，点P在CD上运动（包括端点），则AP·DM的取值范围是.

图4

解（1）以C为坐标原点，CA，CB分别为x轴和y轴建立如图5所示的直角坐标系，易知A（1，0），N0，12，M12，12，设P（x，y），则x≥0，y≥0，x+y≤1，AN=-1，12，MP=x-12，y-12，所以AN·MP=-x+12y+14.

图5

根据线性规划可得AN·MP∈-34，34.

（2）以A为坐标原点，AB为x轴建立如图6所示的直角坐标系，则A（0，0），B（2，0），D12，32，M（1，0），设Px，3212≤x≤52.

图6

所以AP=x，32，DM=12，-32.

从而AP·DM=x，32·12，-32=12x-34.

因为12≤x≤52，所以AP·DM∈-12，12.

点评当向量的模或夹角不明确，且所给平面图形方便建立直角坐标系，并容易写出各涉及点坐标时，常常利用坐标法将向量坐标化求数量积.

三、分解转化基底法

平面向量基本定理：如果e1，e2是同一个平面内两个不共线的向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1，λ2，使a=λ1e1+λ2e2.其中我们把不共线的两个向量e1，e2叫做这一平面内所有向量的一组基底.

例4在Rt△ABC中，C=90°，AC=4则AB·AC=.

解C=90°，AC·CB=0，AB·AC=（AC+CB）·AC=AC2+AC·CB=42=16.

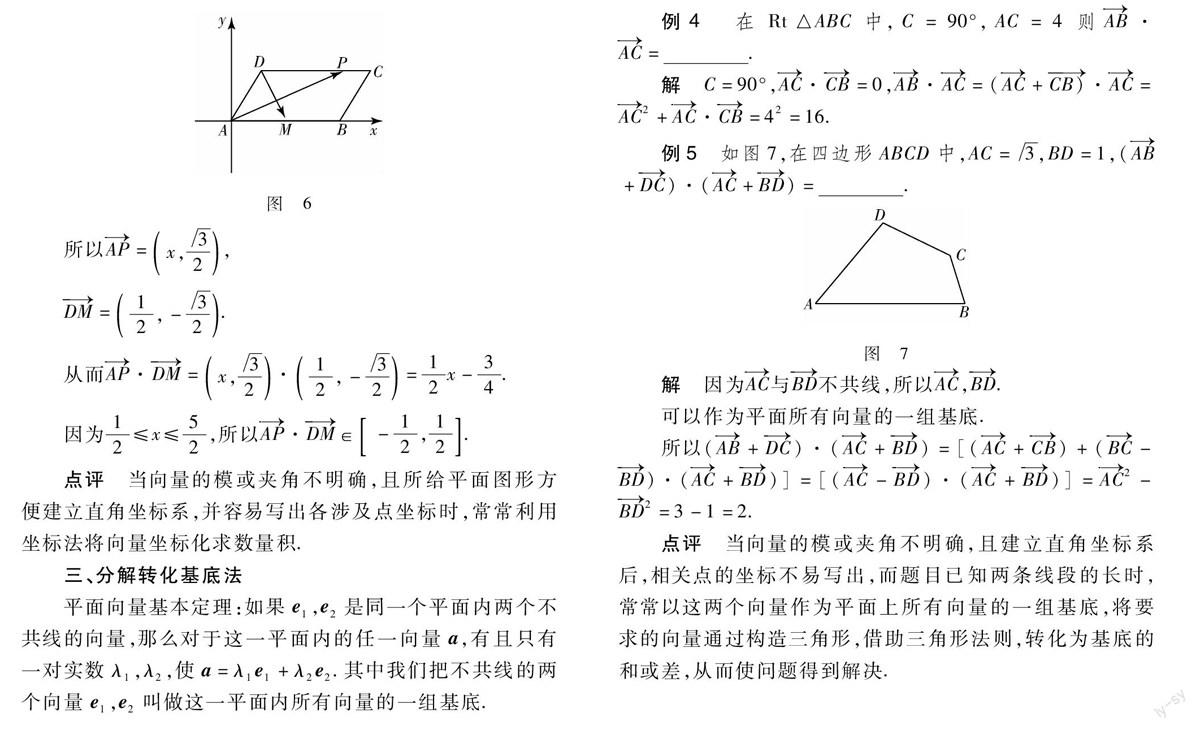
例5如图7，在四边形ABCD中，AC=3，BD=1，（AB+DC）·（AC+BD）=.

图7

解因为AC与BD不共线，所以AC，BD.

可以作为平面所有向量的一组基底.

所以（AB+DC）·（AC+BD）=[（AC+CB）+（BC-BD）·（AC+BD）]=[（AC-BD）·（AC+BD）]=AC2-BD2=3-1=2.

点评当向量的模或夹角不明确，且建立直角坐标系后，相关点的坐标不易写出，而题目已知两条线段的长时，常常以这两个向量作为平面上所有向量的一组基底，将要求的向量通过构造三角形，借助三角形法则，转化为基底的和或差，从而使问题得到解决.