谈初中物理问答题教学

林建富

摘 要：问答题能较好地提高学生的说理、分析、书面表达和总结能力。对学生思维能力发展也有促进作用。本文就初中物理常见的八种类型问答题的教学展开研究，提出各种类型问答题教学的基本思路。

关键词：问答题；教学；初中物理

问答题作为一种对学生说理训练的题型，它能较好地提高学生的说理、分析、书面表达和总结能力，对学生的思维能力的发展也是一种有益的促进 [1 ]。然而，平时作业训练中常出现学生对问题实际性分析和概括不到位，语言表达混乱或三言两语，说不到点子上，教师批改麻烦。这种学生怕教师避的现象，严重影响问答题教学。因此开展对问答题教学的研究就显得很有必要。

1 问答题的分类

问答题形式是多样的，按照它们的不同特点可作如下分类。

■

2 复杂问答题及其教学

简单问答题一般属于基本概念和规律的复述或者是以实际事例和现象来说明基本概念和规律的。它的教学比较容易，这里就不再讨论了，下面着重研究复杂问答题的教学。

2.1 判断性问答题的教学

判断性问答要求按问题给出的条件，运用适当的物理规律和概念进行明确的分析判断，从而得到正确的结论 [2 ]。所以在教学中首先必须使学生弄清所要判断的问题是什么？所给的条件是什么？然后引导学生寻找判断的依据是什么？由此启发学生找到条件、依据和所要判断的问答三者间的内在联系，最后归纳出结论。为使学生易于掌握，一般可采用列表法。

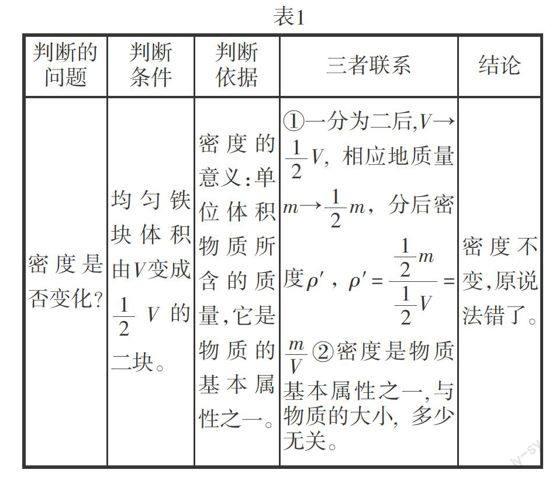
例一（是非型）有人说把一块铁分成相等的两块，铁的密度就成了一半，这个说法对吗？

教学表式如表1

教师在引导学生将所列表格顺次填好后，就可以指导学生将表中条件、依据、联系、结论用适当的词句联结起来构成完整的答案。从而逐步培养学生的表达能力。

答：把一块铁分成相等的两块，这时铁的体积由V变成■V的二块，相应的质量由m变成■m。根据密度的意义，密度等于单位体积物质所含的质量的多少，因而分后密度ρ′=■m/■V=m/V=ρ，即均匀铁块分后密度是不变的。所以原说法不对。

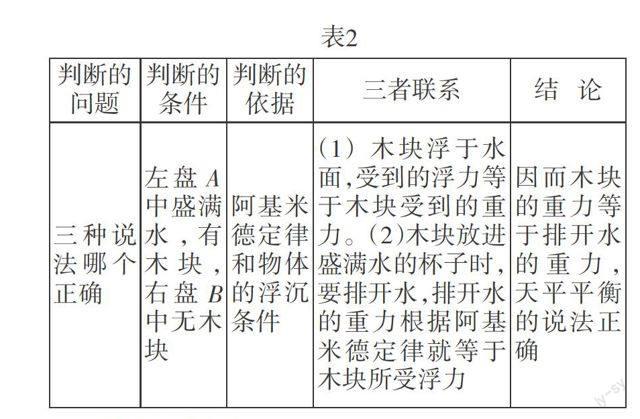
例二 （选择型）有两只同样的烧杯A和B，都盛满水。其中A杯水面上浮着一块木块。把A、B两杯放到天平的左右盘上。大多数同学认为A杯内多一块木块应重些，左盘下降；有的认为木块放在水中要排开一些水，而水的密度大于木块，因而A杯轻。左盘上升；还有的认为A和B一样重，天平平衡。你看谁的说法正确。为什么？

教学表式如表2

在指导学生填写好上述表格后，即可联结成完整答案（答案略）。最后还可以请学生回答其他二个说法错在哪里？可以收到更好的教学效果。

例三 （改错型）用密度大于1×103kg/m3的塑料制成的杯子，放入水中一定沉没水底。这个说法错在哪里？

改错型判断问答题同样可以采用表格式教学。列出判断的问题，判断的条件，判断的依据，三者间的内在联系，结论等栏。让学生分析填写，然后整理组成答案。一般要求，明确指出错在哪里？同时给出正确的说法。

答：用密度大于1×103kg/m3的塑料制成的杯子放入水中，由于物体的浮沉是由浮沉条件决定的，当浮力小于重力时物体下沉；当浮力等于重力时物体或浮于液面或悬浮于液体之中；当浮力大于重力时物体上浮，但随着上浮，浮力不断减小，最后当浮力等于重力时，物体浮于液面。现在杯子重力等于V杯ρ塑g，杯子受到水的浮力等于V杯浸ρ水g。虽然ρ塑>ρ水，但V杯浸无法肯定。因而可能出现几种情况：当V杯浸ρ塑g>V杯浸ρ水g时杯子下沉；当V杯ρ塑g=V杯浸ρ水g时，杯子漂于水面或悬浮于水中；杯子全部浸入后V杯ρ塑g>V杯浸ρ水g则杯子沉入水底。因此该说错在“一定”二字上。正解的应说具有沉入水底的可能，或者说不一定沉入水底。

教学中应指出对改错题的回答答案并不是单一的，必须抓住错误的实质加以改正。同时应鼓励学生多思考，注意培养灵活应用基本概念和规律的能力。

2.2 论述性问答题的教学

论述性问答题要求对问题的物理现象用物理概念和规律或者利用必要的物理模型等进行说理、解释或者论证。在教学中可分为三步进行。第一步是分清物理理象及其物理过程以及它们所处的具体条件。第二步引导分析产生该现象的原因 [3 ]。确定所要运用的物理概念、规律和模型 ，第三步是推理论证，揭示本质。

例四 （解释型）冬天人盖棉被为什么觉暖和？而在夏天储存运输棒冰、雪糕等也要用到棉垫子，为什么？

我们仍可利用表格式进行分析论证，如表3。

在分析填表的基础上，要求学生归纳成文。

例五 （说理型）游泳时用手和脚不断向后划水，人就不断前进，这是为什么？

答：游泳时不断地用手和脚向后划水，水不断地受到手和脚对它的作用力，由于力的作用是相互的，与此同时水就不断地有向前的力作用于手和脚，从而克服了水对人的阻力，使人不断前进。

例六（论证型）用砖砌墙，若砖和灰沙的密度都是ρ。求证墙对地面的压强与墙高成正比，和墙长、墙宽无关。

分析：墙对地的压强决定于墙对地的压力和墙跟地的接触面积，由于墙和地面垂直，墙对地的压力等于墙的重力，而墙的重力G=Vρg，V是墙的体积，它等于Sh，h是墙高，S是墙的截面积，它就应是墙与地的接触面积。论证方法如下：

墙对地压强P=F/S，∵F=G=Vρg ∴P=Shρg/S=hρg。由此知压强正比于墙高，而和墙长、墙宽无关。

2.3 计算性问答题的教学

计算性问答要求按问题所给条件，根据物理概念和规律，通过适当的计算来解释现象，说明道理或者验证规律。这是它区别于一般计算题的方面。在教学中应注意这一不同，要强调分析计算结果的物理意义。（用以解释现象，说明道理、验证规律）

例七 （计算性问答）如图1所示，若立方体每边长2cm。立方体下表面离水面分别为10cm，5cm，1cm。试通过计算验证阿基米德定律。

解：通过计算验证阿基米德定律，意味着由计算得出作用在此立方体上浮力在上述三种情况上都等于该物体排开液体的重力（引导学生认真审题，弄清题目的物理实质）。

在立方体下表面离水面10cm时，该物体完全浸没水中。上表面所受压强P1=P0+h1ρg，下表面所受压强P2=P0+h2ρg。式中P为大气压，h1=8cm，h2=10cm， ρ=1×103kg/m3，g=9.8N/kg。物体所受浮力是上、下表面的压力差（要强调这一基本概念）。F=（p2-p1）S=（h2-h1）·ρgS=7.84×10-2N。此时，立方体排开水的体积V=8×10-6m3，这些水的重力G=Vρg=7.84×10-2N，因而F=G。表明物体所受浮力等于该物体排开液体的重力（明确计算结果的物理意义）。

当立方体下表面离水面5cm时，该物体仍全部浸没水中。因而排开水的体积仍为8×10-6m3，其重力G=7.84×10-2N。物体所受浮力：

F=（5-3）×10-2×1×103×9.8×4×10-4N=7.84×10-2N，因而F=G。这表明只要物体全部浸没在液体中，则浮力的大小与物体浸入的深度无关，总等于该物体排开液体的重力（指明计算结果的物理意义）。

当立方体下表面离水面1cm时，该物体只有一半浸放入水中，因而排开水的重力G′=3.92×10-2N。此时，上表面所受压强p3=p0，下表面所受压强p4=p0+h4 ρg。h4=cm。故浮力F′=（P4-P3）S=h4 ρgS=1×10-2×103×9.8×4×10-4N=3.92×10-2N，所以F′=G′，同样表明物体所受浮力等于该物体排开液体的重力。

综上可知：浸在液体中物体所受的浮力等于该物体排开液体的重力。这就是阿基米德定律。

2.4 实验性问答题的教学

它要求学生观察实验现象，分析实验结果，通过推理判断达到对物理规律、物理概念的进一步认识。因此在教学中应引导学生明确实验的条件和研究途径，仔细观察实验现象，分析实验结果，得出相应的结论，必要时还应加以讨论。

例八 （验证型）把一叠棋子放在桌面上，用手指迅速弹出桌面上的另一只棋子用以冲击最底层的那个棋子，你会看到什么现象？为什么？

观察到的实验现象：可将底层棋子击出，而上面的一叠棋子不倒。

分析：底层棋子被击出，是由于它受到了另一棋子的冲击作用。上面的一叠棋子不倒是由于这叠棋子未受到冲击力的作用，因而将保持它原来的运动状态，这样手指弹的那个棋子在取代底层棋子时，上面的一叠棋子基本上可以保持不动。这就验证了惯性定律。

思考与讨论：（1）如果打击比较轻和慢，情况又将如何？为什么？

（2）选用光滑棋子和选用非常粗糙的棋子来做实验，结果是否一样？为什么？

总之，利用表格形式进行问答题的入门教学可以为学生指出相应的思考分析途径，逐渐形成思考习惯，效果较好。但在学生比较熟悉这种思考分析的途径之后，就不必再书写出来。此外我们还应看到不同类型的问答题有时是互相交叉的，适当修改某些词句，它们可以变换转化为另一类型 。

参考文献：

[1]李文香.小议初中物理问答题教学[J].学周刊，2010（2）.

[2]刘大利，扬杰.浅析物理问答题[J].数理化学习（初中），2003（4）.

[3]王跃民.物理简答题的分析与解答[J].中学理科（初中），2006（3）.