谈如何创设情境提高高中数学课堂教学的有效性

邢昭良

【摘要】《普通高中数学课程标准》指出：“教材应注意创设情境，从具体实例出发，展现数学知识的发生、发展过程.使学生能够从中发现问题、提出问题，经历数学的发现和创造过程，了解知识的来龙去脉.”在有限的课堂教学里，要提高高中数学课堂教学的有效性，更应该下工夫研究问题情境创设.

【关键词】高中数学；教学方法；课堂教学

众所周知，数学是一门思维的科学.于是数学的教学自然而然就是一种思维的教学了.在课堂教学中，引导学生以知识为载体进行充分的思维活动就是老师的主要任务.而思维来自于什么呢？来自于问题.所以对于一节课来说，如何在开头以一个巧妙的问题切入，使学生一下子就进入活跃的思维状态是一节课成败的关键.下面，以我在教学中的实践经验例谈如何巧妙创设情境，提出有效问题激发学生的思维活动，提高课堂教学的有效性.

一、创设趣味问题情境，深刻理解相关概念

《普通高中数学课程标准》在“教学建议”中指出：“教学中应强调对基本概念和基本思想的理解和掌握，对一些核心概念和基本思想（如函数、空间观念、运算、数形结合、向量、导数、统计、随机观念、算法等）要贯穿高中数学教学的始终，帮助学生逐步加深理解.由于数学高度抽象的特点，注重体现基本概念的来龙去脉.在教学中要引导学生经历从具体抽象出数学概念的过程，在初步运用中逐步理解概念的本质.”因此新的基本概念的出现，应下大工夫创设趣味问题情境，让学生饶有兴趣地经历从具体实例抽象出数学概念的过程.

案例一

在学习概率部分时，为了更好地理解独立事件与互斥事件这一概念，我使用了以下情境问题引入：

一位王子向智慧公主求婚，智慧公主为了考验王子的智慧，就让仆人端来两个盘，其中一个装着10枚金币，另一个装着10枚同样大小的银币.仆人把王子的眼睛蒙上，并把两个盘的位置随意调换，请王子随意选一个盘，从里面挑选出一枚硬币.如果选中的是金币，公主就嫁给他；如果选中的银币，那么王子就再也没有机会了.王子听了说：“能不能在蒙上眼睛之前，任意调换盘里的硬币组合呢？”公主同意了.请问：王子该怎样调换硬币才能确保更有把握娶到公主呢？

经过计算发现，把银币放入金币的盘里或两个盘互换几个时，摸到金币的概率都会小于0.5；而把金币放入银币的盘里时，摸到金币的概率会大于0.5.于是产生了一个新的问题：放几个时，摸到金币的可能性最大？经过计算发现，放1个的概率<放2个的概率<放3个的概率<……但如果把金币全部放入概率又回到了0.5.于是得到最终的调换方案如下：

王子在装有金币的盘里留1枚金币，把另外9枚金币倒入放银币的盘里，这样原来放银币的盘里就有10枚银币和9枚金币.如果他选中那个放1枚金币的盘，选中金币的概率为100%；如果选中放19枚钱币的盘，摸到金币的概率为9[]19.王子选中每个盘的概率均为1[]2，所以王子选中金币的概率就是100%×1[]2+9[]19×1[]2=14[]19.如果不做任何调换，王子摸到金币的概率只有1[]2，显然，调换后王子摸到金币的概率大大增加.计算中互斥事件和独立事件不可避免地出现了，于是互斥事件有一个发生的概率以及独立事件同时发生的概率在不知不觉中在应用中学习了.

二、创设关联问题情境，引导学生创新发现

《普通高中数学课程标准》在“教学建议”中还指出：“高中数学课程是以模块和专题的形式呈现的.因此，教学中应注意沟通各部分内容之间的联系，通过类比、联想、知识的迁移和应用等方式，使学生体会知识之间的有机联系，感受数学的整体性，进一步理解数学的本质，提高解决问题的能力.”

案例二

在学习“导数”这一概念时，我创设了这样的问题情境：

1.如何求过圆x2+y2=10上一点P（1，3）的圆的切线方程？（注：可以利用圆的切线性质或圆心到切线的距离等于半径求得）

2.如何求过抛物线y=x2上的点P（1，1）的抛物线的切线方程？（注：可以利用直线与椭圆联立，判别式为0求得）

3.如何求过曲线y=x3上的点P（1，1）的曲线的切线方程？

利用几何画板，要解决的问题直观地呈现给学生：

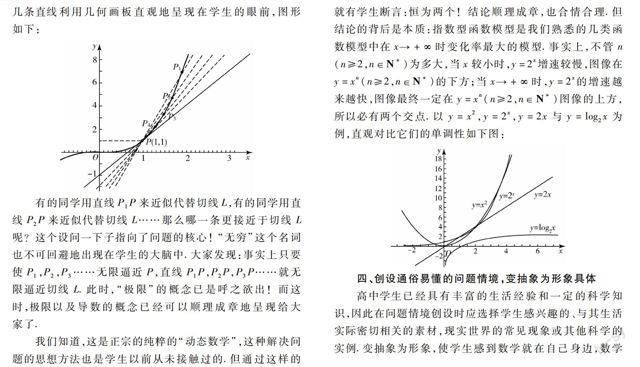
我们要求的就是图中P点处切线L的方程，现在的难点在于无法精确求得，于是提出问题：近似求得L的方程呢？学生都认为这没问题！而且一下子求出了很多，选择几条直线利用几何画板直观地呈现在学生的眼前，图形如下：

有的同学用直线P1P来近似代替切线L，有的同学用直线P2P来近似代替切线L……那么哪一条更接近于切线L呢？这个设问一下子指向了问题的核心！ “无穷”这个名词也不可回避地出现在学生的大脑中.大家发现：事实上只要使P1，P2，P3……无限逼近P，直线P1P，P2P，P3P……就无限逼近切线L.此时，“极限”的概念已是呼之欲出！而这时，极限以及导数的概念已经可以顺理成章地呈现给大家了.

我们知道，这是正宗的纯粹的“动态数学”，这种解决问题的思想方法也是学生以前从未接触过的.但通过这样的情境设置，学生能够以一种最自然的方式认识它、接受它，进而深深植根融合于他们已有的知识体系之中，也为后面顺利探究定积分以及微积分基本定理提供了一次示范.

三、创设感兴趣的问题情境，激发学生探究热情

在数学教学中，应注重发展学生的应用意识；通过丰富的实例引入数学知识，引导学生应用数学知识解决实际问题，经历探索、解决问题的过程，体会数学的应用价值.帮助学生认识到：数学与我有关，与实际生活有关，数学是有用的，我要用数学，我能用数学.从而激发学生的数学探究热情.

案例三

在学习指数函数时，为了给学生指数函数的单调性变化速度的一个精准认识（与幂函数与对数函数的比较），我先在教学中选择了一个这样的生活化情境问题（来自百度）：

一张足够大的普通薄纸，把它一直对折，折30次后有多高？

答案是不可思议的！计算如下：

一张普通的薄纸大约厚度为0.08 mm，

0.08×230÷1000=85899.34592（m），大约相当于10个珠穆朗玛峰高！

为真正认识清楚指数函数与幂函数递增区别，设置以下问题：函数y=2x与函数y=xn（n≥2，n∈N*）在第一象限有几个交点？

学生的直觉都是错误的.于是化繁为简：就最简单的y=2x与y=x2（即n=2时）的图像在第一象限的交点有几个呢？通过计算和几何画板展示有两个交点.之后趁热打铁：n=3呢？n=4呢？经过一番探究，有几个悟性较高的学生发现交点是两个.检验是简单的，几何画板直观明了毫无争议.之后拓展升华：对一般的n（n≥2，n∈N*）呢？马上就有学生断言：恒为两个！结论顺理成章，也合情合理.但结论的背后是本质：指数型函数模型是我们熟悉的几类函数模型中在x→+∞时变化率最大的模型.事实上，不管n（n≥2，n∈N*）为多大，当x较小时，y=2x增速较慢，图像在y=xn（n≥2，n∈N*）的下方；当x→+∞时，y=2x的增速越来越快，图像最终一定在y=xn（n≥2，n∈N*）图像的上方，所以必有两个交点.以y=x2，y=2x，y=2x与y=log2x为例，直观对比它们的单调性如下图：

四、创设通俗易懂的问题情境，变抽象为形象具体

高中学生已经具有丰富的生活经验和一定的科学知识，因此在问题情境创设时应选择学生感兴趣的、与其生活实际密切相关的素材，现实世界的常见现象或其他科学的实例.变抽象为形象，使学生感到数学就在自己身边，数学应用无处不在.

案例四

我在讲解“二分法”时，设置了这样的问题情境：授课前，我准备了一台价值67元的计算器.创设问题为：已知这台计算器的价格在200元之内，如果谁能在10秒之内猜出这台计算器的价格，我就把这台计算器送给这名同学.

经过大家几番共同的修正与改进，发现最快的猜测如下：先猜100（这是0与200的中间数，此时我会说高了），然后猜50（这是0与100的中间数，此时我会说“低了”），然后再猜75（这是50与100的中间数，此时我会说“高了”），然后猜60（低了），然后猜70（高了），然后猜65（低了），然后即马上猜中.

这里用到的方法就是数学中典型的“二分法”.通过这样一个具体的情境浅显地呈现于大家的面前后，再讲解课本中应用于数学里“二分法”就使学生很容易接受.它使抽象的方法变得形象具体，使学生觉得马上就可以动手操作.

创设有效的问题情境，不仅能够激发学生的学习兴趣，而且能够培养学生自主地探索、解决问题的能力.教师在数学教学过程中要了解学生不喜欢数学的原因，并要善于挖掘教材潜力，下大工夫创设美好的数学情境教学，以便激励、唤醒、鼓舞学生，激发学生饱满的学习热情，促使他们以积极的态度和旺盛的精力主动求索，从而获得课堂教学的最佳效果.

【参考文献】

[1]普通高中数学课程标准研制组.普通高中数学课程标准.人民教育出版社，2003：108-117.

[2]张燕顺.数学的思想、方法和应用（修订版）.北京：北京大学出版社，2005：249-272.