具有耐药性肺结核病模型的稳定性分析

宋运娜

（齐齐哈尔医学院高等数学教研室，黑龙江 齐齐哈尔 161006）

具有耐药性肺结核病模型的稳定性分析

宋运娜

（齐齐哈尔医学院高等数学教研室，黑龙江 齐齐哈尔 161006）

研究具有耐药性肺结核病模型的稳定性，建立了8维传染病模型.运用基本再生矩阵的谱半径和Lyapunov函数，得到模型的无病平衡点、边界平衡点和地方病平衡点存在性和稳定性的充分条件.结果表明：减少耐药性相关系数β2，k2，b2可以控制传染病的蔓延.

耐药性；肺结核；平衡点；传染病模型

耐药性结核病具有治愈率低、治疗时间长、费用高、传染率高、传染性强、对健康人群有较大威胁的特点.根据世界卫生组织调查，每10个结核病人中至少有1人是耐药性的结核病.目前针对结核病的数学模型比较多，Yang等［1］研究了治疗不充分的结核病模型的稳定性；Zhou等［2］研究了受到健康教育和治疗结核病模型的稳定性；Mishra等［3］研究了伴随接种的多重耐药性肺结核疾病；Choi等［4］研究了防控肺结核传播的最优策略的数学模型；刘俊利等［5－6］分析了肺结核病模型的全局稳定性；杨亚莉等［7］考虑了具有外源性感染的结核病模型；Ahmadin等［8］研究了具有耐药性肺结核病模型及其治疗策略.本文拟建立具有耐药性的肺结核病数学模型，研究耐药性对该传染病传播的影响.

1 模型的建立

根据病理过程可将人群分为易感染者S，敏感潜伏者E1，具有耐药性的潜伏者E2，敏感的活动性肺结核病人C1，具有耐药性的活动性肺结核病人C2，敏感的结核病人I1，具有耐药性的结核病人I2，假设具有耐药性的结核病人无法治愈，敏感结核病治愈者为R，可得

其中A表示人口的自然补充率；u，u1，u2分别表示人口的自然死亡率、患敏感肺结核病的死亡率和患耐药肺结核病的死亡率；β1（N），β2（N）分别为敏感和耐药结核杆菌传播易感染者的传染率，其中N为人群总数；k1，k2为敏感和耐药潜伏者转变为活动性肺结核病人的比率；d为敏感活动性肺结核病人的恢复率；b1，b2为具有敏感和耐药性的活动性肺结核病人转变为传染性肺结核病人的比率；敏感的传染性肺结核病人以ap比率转化为活动性肺结核病人，因治疗不当转变为具有耐药性活动性肺结核病人的比率是a（1－p），式中a为敏感肺结核病人的转移率.若（1）式中各参数初始值均大于0，则N′＝（S＋E1＋E2＋C1＋C2＋I1＋I2＋R）′＝A－u N1－u1I′－u2I′2，故N′≤A－u N，从而0＜N（t）≤A／u＋N0e－ut，式中N0表示人口总数的初值，N（t）表示t时刻人口总数.同理，S（t），E1（t），E2（t），C1（t），C2（t），I1（t），I2（t），R（t）分别表示t时刻各类人口数.当0＜N（t）＜A／u时，（1）式中所有 解 进 入 区 域Γ＝ ｛（S（t），E1（t），E2（t），C1（t），C2（t），I1（t），I2（t），R（t））∈R8＋：N（t）＜A／u｝.因（1）式中第1～7方程中不含R，故可简化为

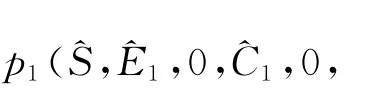
2 无病平衡点的存在性和全局稳定性

改变变量顺序，即E1，C1，I1，E2，C2，I2，可得矩阵

则基本再生矩阵FV－1的主特征值的绝对值为

矩阵FV－1的谱半径ρ（FV－1）＝max｛R1，R2｝，R1＜1，R2＜1，则ρ（FV－1）＜1.由文献［9］知无病平衡点p0是局部渐近稳定的，下面证明p0的全局渐近稳定性.构造Lyapunov函数v1（E1，C1，I1，E2，C2，I2）＝b2k2E2＋（u＋k2）u I2＋k2b2E1＋（u＋k1）（u＋d＋b1）I1＋（u＋k1）b1C2，v′1＝b2k2E′2＋（u＋k2）·u I′2＋k2b2E′1＋（u＋k1）（u＋d＋b1）I′1＋（u＋k1）b1C′2＝u（u＋k2）（u＋u2）（R1－1）I2＋（u＋u1）［u2＋（b1＋a＋u1）u＋da＋b1u1＋b1a＋du1－ab1p］（R1－1）I1－u（u＋b2）b2C2＋b2k2E2（u＋d＋b1）＋（u＋k1）（u＋d＋b1）b1C1－b2k2（u＋k1）E1＋b1（u＋k1）［k2E2－（u＋b2）C1＋a I1］.（2）式中不可治愈耐药性肺结核病人的数量远远少于敏感性肺结核病人数，即C2≪C1，耐药性主要因治疗不当引起，可设E2≪C2，敏感性肺结核病中I1＜C1≪E1，则－u（u＋b2）b2C2＋b2k2E2（u＋d＋b1）＜0，（u＋k1）（u＋d＋b1）b1C1－b2k2（u＋k1）E1＜0，k2E2－（u＋b2）C1＋a I1＜0.当R1＜1，R2＜1时，v′1＜0.此时（2）式最大不变子集是无病平衡点p0.由LaSalle不变集原理知，（2）式无病平衡点p0（S0，0，0，0，0，0，0，0）全局渐近稳定.

3 边界平衡点的存在性及稳定性

当不存在耐药性肺结核疾病时，模型为

求解得

将（5）式代入（4）式第3个方程中，可得

4 地方病平衡点的存在性和稳定性

令（2）式各方程为0，得

5 结论

［1］YANG Yali，LI Jianquan，MA Zhien，et al.Global stability of two models with incomplete treatment for tuberculosis［J］.Chaos Soliton Fract，2010，43（1／12）：79－85.

［2］ZHOU Xueyong，SHI Xiangyun，CHENG Huidong.Modelling and stability analysis for a tuberculosis model with healthy education and treatment［J］.Comp Appl Math，2013，32（2）：245－260.

［3］MISHRA B K，SRIVASTAVA J.Mathematical model on pulmonary and multidrug－resistant tuberculosis patients with vaccination［J］.J Egyptian Math Soc，2014，22（2）：311－316.

［4］CHOI S，JUNG E.Optimal tuberculosis prevention and control strategy from a mathematical model based on real data［J］.Bull Math Biol，2014，76（7）：1566－1589.

［5］LIU Junli，ZHANG Tailei.Global stability for a tuberculosis model［J］.Math Comput Model，2011，45（1／2）：836－845.

［6］刘俊利.一个具有干预策略的肺结核模型的阈值动力学行为 ［J］.生物数学学报，2011，26（4）：601－608.

［7］杨亚莉，郭晨平，黄利航，等.一类考虑外源性再感染的结核病模型 ［J］.生物数学学报，2014，29（4）：597－602.

［8］AHMADIN，FATMAWATI.Mathematical modeling of drug resistance in tuberculosis transmission and optimal control treatment［J］.Appl Math Sic，2014，8（92）：4547－4559.

［9］DRIESSCHE P，WATMOUGH J.Reproduction numbers and sub－threshold endemic equilibria for compartmental models of disease transmission［J］.Math Biosci，2002，180（1／2）：29－48.

Stability analysis of pulmonary tuberculosis model with resistance

SONG Yunna

（Math Staff Room，Qiqihar Med Coll，Qiqihar 161006，China）

The stability analysis of pulmonary tuberculosis model with resistance is investigated.Pulmonary tuberculosis is divided into three classes：lurker，activity in patients with pulmonary tuberculosis and infectious tuberculosis patients.8 dimensional model of infectious disease is established to study the patient’s drug resistance.Using the spectral radius of the basic reproduction matrix and the Lyapunov function，the sufficient conditions for the existence and stability of the disease－free equilibrium of the model，boundary equilibrium and the endemic equilibrium were obtained.The results show that the spread of pulmonary tuberculosis can be controlled by reducing the coefficientβ2，k2andb2.

drug resistance；pulmonary tuberculosis；equilibrium point；epidemical model

O 29；R 521

A

1007－824X（2015）03－0024－04

2014－12－11.E－mail：songyunna1999＠163.com.

黑龙江省教育厅科研项目（12521647）；齐齐哈尔医学院青年基金项目（QY2013－02）.

宋运娜.具有耐药性肺结核病模型的稳定性分析 ［J］.扬州大学学报（自然科学版），2015，18（3）：24－27.

（责任编辑 秋 实）