一类CSL代数上的完全有界上同调群

李 俊，陈 琳，2＊

（1.安顺学院数理学院，贵州 安顺 561000；2.苏州大学数学科学学院，江苏 苏州 215006）

一类CSL代数上的完全有界上同调群

李 俊1，陈 琳1，2＊

（1.安顺学院数理学院，贵州 安顺 561000；2.苏州大学数学科学学院，江苏 苏州 215006）

设L是可分Hilbert空间H上由有限多个无关的套生成的交换子空间格，Alg L是其对应的子空间格代数.证明了系数在超弱闭Alg L双模（包含Alg L）上的n阶完全有界上同调群是平凡的.

有限宽；CSL代数；完全有界上同调群

导子作为算子代数上的重要映射［1－3］，对算子代数上导子内性的研究实际上是探讨算子代数上的一阶上同调群是否平凡.1972年，Johnson［4］从上循环的角度确立了Banach代数上的上同调理论.此后，计算算子代数上的上同调群成为算子代数研究的一个重要内容.Forrest等［5］给出了系数在其对偶双模的三角Banach代数上的2阶上同调群的计算，Grønbæk［6］证明了系数在其对偶双模的具有与矩阵代数相似结构的一类Banach代数上的n阶上同调群是平凡的，Feizi等［7］对系数在其双模的Beurling代数上的n阶上同调群进行了研究，Lance［8］证明了系数在其双模的套代数上的n阶上同调群是平凡的，Hou等［9］证明了系数在其双模的套代数上的n阶完全有界上同调群是平凡的.本文主要证明由有限多个无关套生成的交换子空间格（CSL）对应的交换子空间格代数（CSL代数）上的完全有界上同调群是平凡的.

1 预备知识

设A是含单位元I的Banach代数，M是含单位元的Banach A双模.对正整数n，Cn（A，M）表示从A×A×…×A到M的有界n重线性映射构成的线性空间，Cn（A，M）中的元素称n上链.∀φ∈Cn（A，M），定义上边缘算子δ：Cn（A，M）→Cn＋1（A，M）为

本文中，B（H）表示复数域上Hilbert空间H上的有界线性算子的全体.∀x，y∈H，秩一算子x⊗y定义为：z〈z，y〉x，∀z∈H.设L是H的一族闭子空间，若它包含0和H，并且在集合交和集合并的闭包运算下封闭，则称L是H上的子空间格.若L中的任意两个元素关于乘法可交换，则称L为交换子空间格，简记为CSL，其对应的交换子空间格代数简称为CSL代数.设L是H上的子空间格，定义其对应的子空间格代数Alg L＝｛T∈B（H）：TP⊆P，∀P∈L｝.全序的子空间格称为套，其对应的子空间格代数称为套代数.关于套代数，子空间格代数的详细内容可参见文献［10］.设L是一个套，定义

2 主要结果

情形1Ω＝Ø，即∀i∈｛1，2，…，n｝，有≠I.令.由 L1，L2，…，Ln是无关的套，知N≠0.选取y∈N且‖y‖＝1，∀x∈H，由文献［12］中引理1，得x⊗y∈Alg L.对任意A1，…，An－1∈Alg L，定义φ∈Cn－1（Alg L，B（H））为φ（A1，…，An－1）x＝（－1）nσ（A1，…，An－1，x⊗y）y.于是，由得

这说明δφ＝σ.下证φ完全有界.当k＝1时，由

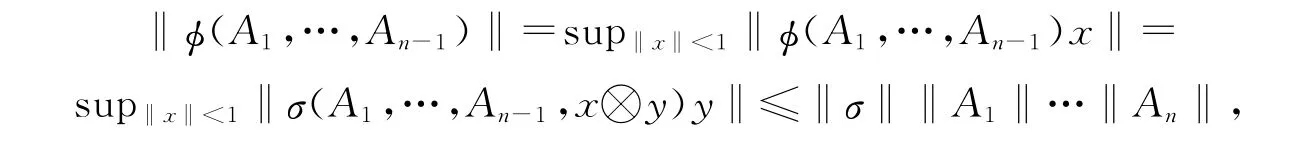
得‖φ‖≤‖σ‖.当k≥2时，令M k（Alg L）表示Alg L上k×k阶算子矩阵B＝［B（i，j）］的全体，其中B（i，j）是B的第i行第j列位置的元素.定义n－1重线性映射φk：M k（Alg L）×M k（Alg L）×…×M k（Alg L）→M k（B（H））≅B（Hk）为

其中B l＝［B l（i，j）］∈Mk（Alg L），l＝1，…，n－1.取x＝（x1，…，x k）τ∈Hk，且‖x‖≤1，于是

这说明φk（B1，B2，…，B n－1）x＝（－1）nσk（B1，…，B n－1，B n）y，其中y＝（y，0，…，0）τ.从而，

［1］AYUPOV SH，KUDAYBERGENOV K.2－local derivation and automorphisms onB（H）［J］.J Math Anal Appl，2012，395（1）：15－18.

［2］CHEN Lin，LU Fangyan.Local Lie derivation of nest algebras［J］.Linear Algebra Appl，2015，475：62－72.

［3］HOU Chengjun.Derivations of a class of Kadison－Singer algebras［J］.Linear Algebra Appl，2015，466：241－253.

［4］JOHNSON B E.Cohomology in Banach algebras［M］.Providence R I：American Mathematical Society，1972：1－96.

［5］FORREST B E，MARCOUX L W.Second order cohomology of triangular Banach algebras［J］.Houston J Math，2004，30（4）：1157－1176.

［6］GRØNBÆK N.Bounded Hochschild cohomology of Banach algebras with a matrix－like structure［J］.Trans Amer Math Soc，2006，358（6）：2651－2662.

［7］FEIZI E，POURABBAS A.On the Hochschild cohomology of beurling algebras［J］.Bull Belg Math Soc Simon Stevin，2006，13（2）：305－318.

［8］LANCE E C.Cohomology and perturbations of nest algebras［J］.Proc London Math Soc，1981，43（2）：334－356.

［9］HOU Chengjun，WEI Cuiping.Completely bounded cohomology of non－selfadjoint operator algebras［J］.Acta Math Sci：Engl Ed，2007，27（1）：25－33.

［10］LU Fangyan.The Jordan structure of CSL algebras［J］.Studia Math，2009，190（3）：283－299.

［11］TAKESAKI M.Theory of operator algebra I［M］.New Yock－Berlin Heidelberg：Springer－Verlag，1979：188－192.

［12］LU Fangyan.Lie derivations of certain CSL algebras［J］.Israel J Math，2006，155：149－156.

Completely bounded cohomology of certain CSL algebra

LI Jun1，CHEN Lin1，2＊

（1.Sch of Math ＆Phys，Anshun Coll，Anshun 561000，China；2.Sch of Math Sci，Soochow Univ，Suzhou 215006，China）

Let L be a commutative subspace lattice generated by finitely many independent nests，and Alg L be the associated CSL algebra.In this paper，it is proved that alln－th completely bounded cohomology groups of Alg L acting on separate Hilbert space are trivial when the coefficients lie in any ultra－weakly closed Alg L－bimodule containing Alg L.

finite width；CSL algebra；completely bounded cohomology

O 177.1

A

1007－824X（2015）03－0016－04

2015－01－12.＊ 联系人，E－mail：linchen198112＠163.com.

贵州省科技厅－安顺市政府－安顺学院联合科研资助项目（黔科合J字LKA［2013］04号）.

李俊，陈琳.一类CSL代数上的完全有界上同调群 ［J］.扬州大学学报（自然科学版），2015，18（3）：16－19.

（责任编辑 青 禾）