一种改进的有限点集法模拟高阶非线性动力学问题

任金莲，蒋 涛，朱 莹

(扬州大学数学科学学院，江苏扬州 225002)

一种改进的有限点集法模拟高阶非线性动力学问题

任金莲，蒋 涛*，朱 莹

(扬州大学数学科学学院，江苏扬州 225002)

针对高阶非线性动力学问题的求解，提出了一种改进的有限点集法(corrected finite pointsetmethod，CFPM).首先将具有高阶导数的非线性偏微分方程分解为若干一阶偏微分方程，并采用有限点集法对其进行离散求解;然后连续应用低阶导数逐阶逼近高阶导数;最后对比一维非线性黏性Burgers方程及具有高阶导数的KdV-Burgers方程的数值解与解析解，并将二维非线性Burgers方程的数值结果与其他数值结果进行比较.实例分析表明，CFPM方法能够准确、可靠地求解非线性动力学问题.

有限点集法;非线性;黏性Burgers方程;KdV-Burgers方程

非线性动力学问题的研究对于许多物理现象的解释具有重要意义［1-2］.近年来，非线性动力学问题的模拟研究备受关注.Liao［3］采用有限差分法研究了二维Burgers方程;Belytschko等［4］阐述了无网格方法在非线性动力学问题求解方面的应用;Kobert［5］和Tiwari［6］等提出了有限点集方法(finite pointsetmethod，FPM)，并用于求解Poisson方程及非线性Navier-Stokes问题，但对于高阶导数的非线性动力学问题的模拟研究仍处于初级阶段.本文基于文献［7］提出一种改进的有限点集法(corrected finite pointsetmethod，CFPM)以求解高阶非线性偏微分方程动力学问题.

1 问题描述

考虑二维黏性Burgers方程［8］

其中υ为黏性系数，u为速度，u=(u，v).方程(1)的初值条件为u(x，t0)=g0(x)，x=(x，y)∈Ω，边界条件为 L(u(x，t))=φ(x，t)，x∈∂Ω.

一维黏性Burgers方程为

其中 x∈［0，1］.方程(2)的初值条件为 u(x，0)=sin(πx)，边界条件为 u(0，t)=u(1，t)=0.

一维 KdV-Burgers方程［9］为

2 本文方法

将空间的高阶偏导数分解为多个一阶偏导数，以三阶导数为例，有

然后对一阶偏导数进行离散.

在二维空间坐标下，函数f（x）在点x i＝（x i，y i）处的Taylor展开式为

其中m为时间层，m＝0，1，2，…；f（0）（x i）为初值，f k为第k个空间分量的一阶偏导数；f kl，f lk为空间分量k，l的二阶偏导数，f kl＝f lk；ei为截断误差.当i＝1，2，…，n时，有

即J＝ （Ma（m＋1）－b（m））TW（Ma（m＋1）－b（m）），其中W为相邻各点处权函数值构成的对角矩阵，W＝diag（ω1，ω2，…，ωn），ωi为加权系数.进一步根据多维函数极值原理可得

对区域离散点下一时刻值f（m＋1）进行迭代求解，得到其迭代终止条件为

其中ε通常取10－2量级的正值，N为模拟区域中离散点的总数.

3 主要结果

3.1 一维问题的模拟

首先运用CFPM、SPH（smoothed particle hydrodynamics）和CSPH（corrected smoothed particle hydrodynamics）等3种方法求解一维Burgers方程，其中空间步长h＝1.1Δx，时间步长Δt＝10－4s，这里采用非均匀粒子布置.图1给出了υ＝10－1，t＝0.05 s时刻下的速度剖面.由图1可见，CFPM的数值结果更接近解析解，表明该方法数值精度更高，稳定性好，能够准确、可靠地求解一维Burgers方程.

图1 不同方法下的数值结果Fig.1 Comparison of numerical results by different methods

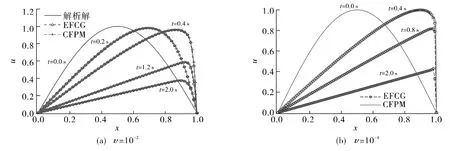
图2 不同黏度下一维Burgers方程的数值结果Fig.2 Numerical results for the 1－D Burgers equation with different viscosity

图2给出了υ＝10－2和υ＝10－4两种情况下采用CFPM和EFCG（element free characteristic galerkin）方法得到的数值模拟结果，这里采用点加密方式以增强模拟的稳定性.由图2可见，CFPM与EFCG的结果吻合，说明CFPM方法能够稳定、准确地捕捉较低黏度时出现的激波现象.

对一维 Kd V－Burgers方程进行模拟，取α＝0.000 9，β＝－0.000 02，计算区间为（－4，4），相应的数值模拟结果如图3所示.由图3可见，CFPM的结果与解析解吻合，表明CFPM方法能够准确捕捉孤立波的传播过程，且可以准确、可靠地求解具有三阶导数的非线性问题.

3.2 二维问题的模拟

假设方程（1）的初边值条件分别为

图3 Kd V－Burgers方程的数值解与解析解Fig.3 The CFPM results for the Kd V－Burgers equation

图4给出了υ＝10－2时不同时刻下二维Burgers方程沿x＝y方向的u速度和v速度曲线.由图4可见，u速度在x＝1附近出现激波间断现象；v速度在x＝0.6与x＝0.8之间出现激波间断现象.CFPM模拟结果与EFCG结果［10］相吻合，表明CFPM能够有效地模拟二维Burgers方程.图5给出了速度u，v的等值线云图.图5显示，u速度和v速度的变化趋势不同且两者变化的复杂度均较高.

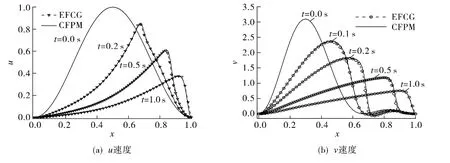
图4 二维Burgers方程沿x＝y方向的数值结果Fig.4 Numerical results for the 2－D Burgers equation along the x＝y direction

图5 不同时刻下的速度等值线云图Fig.5 The velocity contour at different times

4 结论

本文针对非线性动力学问题的求解，提出了一种改进的有限点集方法.通过一维和二维非线性问题的模拟实例，验证了本文方法能够很好地降低传统的有限点集法在求解高阶导数偏微分方程时的复杂度，且精度高、稳定性好，能够准确、可靠地模拟非线性动力学问题，并可有效预测二维Burgers方程解中复杂的激波间断现象.

［1］COLE J D.On a quasi linear parabolic equation occurring in aerodynamics［J］.Quart Appl Math，1951，9（3）：225－236.

［2］OZIS T，AKSAN E N，OZDES A.A finite element approach for solution of Burgers’equation［J］.Appl Math Comput，2003，139：417－428.

［3］LIAO Wenyuan.A fourth－order finite－difference method for solving the system of two－dimensional Burgers’equations［J］.Int J Num Meth Flu，2010，64（5）：565－590.

［4］BELYTSCHKO T，KRONGAUZ Y K，FLEMING D，et al.Meshless methods：an overview and recent development［J］.Comput Meth Appl Mech Eng，1996，139（4）：3－47.

［5］KOBERT M，KUHNER J，KLAR A.Application of the finite pointset method（FPM）to the kinetic BGK model［J］.Proc Appl Math Mech，2012，12（1）：657－658.

［6］TIWARI S，KUHNER J.Modeling of two－phase flows with surface tension by finite pointset method（FPM）［J］.J Comput Appl Math，2007，203（2）：376－386.

［7］蒋涛，欧阳洁，栗雪娟，等.瞬态热传导问题的一阶对称SPH方法模拟 ［J］.物理学报，2010，60（9）：090206.

［8］CHEN J K，BERAUN J E.A generalized smoothed particle hydrodynamics method for nonlinear dynamic problems［J］.Comput Methods Appl Mech Eng，2000，190（1／2）：225－239.

［9］MA Changfeng.A new lattice boltzmann model for Kd V－Burgers equation ［J］.Chin Phys Lett，2005，22：2313.

［10］ZHANG Xiaohua，OUYANG Jie，ZHANG Lin.Element free characteristic Galerkin method for Burgers’equation［J］.Eng Anal Bound Elem，2009，33（3）：356－362.

A corrected finite pointset method for solving the non－linear dynamics problems

REN Jinlian，JIANG Tao＊，ZHU Ying

（Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China）

A corrected finite point－set method（CFPM）is proposed to solve the non－linear dynamics problems in this paper.The improvements in the proposed method are：the high－order partial differentiable equation（PDE）is decomposed into multi－first－order PDE；the obtained first－order PDE is discretized using the finite point－set method（FPM）；the discretization scheme of first－order PDE is continuously used to solve the higher－order PDE.To test the ability and merits of the proposed CFPM，one－dimensional（1D）Burgers equation with analytical solutions，1D Kd V－Burgers equation with three－order derivatives and 2D Burgers equation with initial boundary values condition are solved in turn，and compared with the analytical or other numerical solutions.The numerical results show that the CFPM can accurately and reliably solve the non－linear dynamics problems.

finite pointset method；non－linear；viscous Burgers equation；Kd V－Burgers equation

O 242.1;O 241.7

A

1007-824X(2015)03-0020-04

2014-10-05.* 联系人，E-mail:jtrjl_2007@126.com.

国家自然科学基金资助项目(51309200);江苏省自然科学基金资助项目(BK20130436);中国博士后科学基金面上资助项目(2014M550310).

任金莲，蒋涛，朱莹.一种改进的有限点集法模拟高阶非线性动力学问题［J］.扬州大学学报(自然科学版)，2015，18(3):20-23，36.

（责任编辑 林 子）